Билет 39

Дифференциальное уравнение электромагнитной волны

Одним из важнейших следствий уравнений Максвелла является существование электромагнитных воли. Можно показать, что для однородной и изотропной среды вдали от зарядов и токов, создающих электромагнитное поле, из уравнений Максвелла следует, что векторы напряженностей Е и Н переменного электромагнитного поля удовлетворяют волновому уравнению типа (154.9):

                                                             (162.1)

                                                             (162.2)

где   — оператор Лапласа, v — фазовая скорость.

Всякая функция, удовлетворяющая уравнениям (162.1) и (162.2), описывает некоторую волну. Следовательно, электромагнитные поля действительно могут существовать в виде электромагнитных волн. Фазовая скорость электромагнитных воли определяется выражением

                                                      (162.3)

где с =  ,   и   — соответственно электрическая и магнитная постоянные, e и m — соответственно электрическая и магнитная проницаемости среды.

В вакууме (при e=1 и m=l) скорость распространения электромагнитных волн совпадает со скоростью с. Так как em > 1, то скорость распространения электромагнит­ных воли в веществе всегда меньше, чем в вакууме.

При вычислении скорости распространения электромагнитного поля по формуле (162.3) получается результат, достаточно хорошо совпадающий с экспериментальными данными, если учитывать зависимость e и m от частоты. Совпадение же размерного коэффициента в (162.3) со скоростью распространения света в вакууме указывает на глубокую связь между электромагнитными и оптическими явлениями, позволившую Максвеллу создать электромагнитную теорию света, согласно которой свет представ­ляет собой электромагнитные волны.

Следствием теории Максвелла является поперечность электромагнитных волн: век­торы Е и Н напряженностей электрического и магнитного полей волны взаимно перпендикулярны (на рис. 227 показана моментальная «фотография» плоской электро­магнитной волны) и лежат в плоскости, перпендикулярной векторуv скорости рас­пространения волны, причем векторы Е, Н и v образуют правовинтовую систему. Из уравнений Максвелла следует также, что в электромагнитной волне векторы Е и Н всегда колеблются в одинаковых фазах (см. рис. 227), причем мгновенные значения Е и Н в любой точке связаны соотношением

                                                    (162.4)

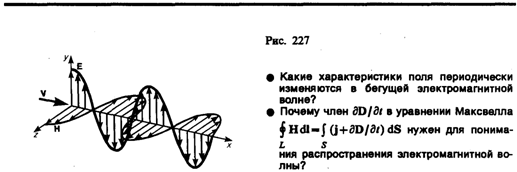
Следовательно, Е и Н одновременно достигают максимума, одновременно обращаются в нуль и т. д. От уравнений (162.1) и (162.2) можно перейти к уравнениям

                                                        (162.5)

                                                       (162.6)

где соответственно индексы у и z при Е и Н подчеркивают лишь то, что векторы Е и Н направлены вдоль взаимно перпендикулярных осей y и z.

Уравнениям (162.5) и (162.6) удовлетворяют, в частности, плоские монохроматические электромагнитные волны (электромагнитные волны одной строго определенной частоты), описываемые уравнениями

                                                          (162.7)

                                                         (162.8)

где E₀ и Н₀ — соответственно амплитуды напряженностей электрического и магнитного полей волны, w — круговая частота волны, k=w/v — волновое число, j — на­чальные фазы колебаний в точках с координатой х=0. В уравнениях (162.7) и (162.8) j одинаково, так как колебания электрического и магнитного векторов в электромагнитной волне происходят в одинаковых фазах.

Плоская электромагнитная волна

Волна называется плоской, если поверхности равных фаз представляют собой плоскость, т.е. в плоской электромагнитной волне векторы   и   расположены в плоскости хода, перпендикулярно направлению распространения волны.

Однородной плоской волной называется волна, в которой при соответствующем выборе осей координат векторы   и   зависят только от одной координаты и времени (рис. 18.4).

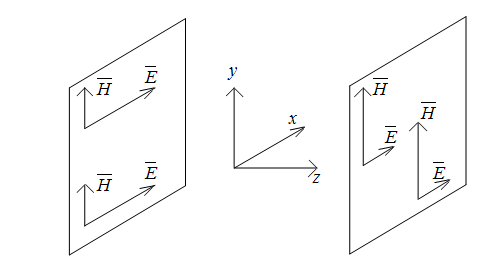
Рис. 18.4. Распространение плоской однородной волны

Если векторы   и   изменяются по синусоидальному закону, то волна называется гармонической или монохроматической.

По определению плоской волны

В плоской волне   и   являются функциями только одной координаты – z. Из системы уравнений (18.12) для синусоидальных функций в комплексной форме записи получается:

(18.14)

Решение линейного дифференциального уравнения второго порядка имеет вид

(18.15)

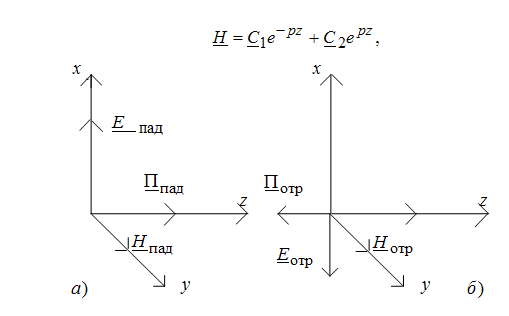
Рис. 18.5. Векторы падающей и отраженной волны электромагнитного поля

Компоненты падающей волны  и   дают вектор Пойнтинга   (рис. 18.4а), направленный по положительной оси z. Следовательно, движение энергии падающей волны происходит вдоль положительного направления оси z. Соответственно отраженная волна на рис, 18.4б несет свою энергию вдоль отрицательного направления оси z.

Волновое сопротивление   можно трактовать как отношение  / . Так как волновое сопротивление является числом и имеет аргумент  , то сдвиг во времени между  и   для одной и той же точки поля равен  .

1.3. Энергия электромагнитных волн

Как показывает опыт, электромагнитные волны могут производить различные действия: нагревание тел при поглощении света, вырывание электронов с поверхности металла под действием света (фотоэффект). Это свидетельствует о том, что электромагнитные волны переносят энергию. Эта энергия заключена в распространяющихся в пространстве электрическом и магнитном полях.

В курсе электричества и магнетизма было показано, что объемная плотность энергии электрического поля равна (1.1)

а магнитного поля –

(1.2)

где   и   – электрическая и магнитная постоянные. Таким образом, полная плотность энергии электромагнитной волны равна

(1.3)

Так как модули вектора напряженности электрического и индукции магнитного поля в электромагнитной волне связаны соотношением  , то полную энергию можно выразить только через напряженность электрического поля или индукцию магнитного поля:

(1.4)

Из (1.4) видно, что объемная плотность энергии складывается из двух равных по величине вкладов, соответствующих плотностям энергии электрического и магнитного полей. Это обусловлено тем, что в электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры».

Плотность энергии электромагнитного поля можно представить в виде:

(1.5)

Формула (1.5) характеризует плотность энергии в любой момент времени в любой точке пространства.

Если выделить площадку с площадью s, ориентированную перпендикулярно направлению распространения волны, то за малое время Δt через площадку пройдет энергия  , равная

,

где   – скорость электромагнитной волны в вакууме.

Плотностью потока энергии называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади, перпендикулярной к направлению распространения волны:

(1.6)

Подставляя в последнее соотношение выражения для   и  , получим

.

Импульс электромагнитного поля

Импульс электромагнитного поля, динамическая характеристика поля — количество движения, которым обладает электромагнитное поле в данном объёме. Тела, помещенные в электромагнитное поле, испытывают действие механических сил. Воздействие поля на тело при этом связано с поглощением телом электромагнитных волн или изменением направления их распространения (отражение, рассеяние, преломление). При излучении телом электромагнитных волн, в частности света, импульс тела также меняется. Так как импульс замкнутой материальной системы в результате излучения, поглощения или отражения электромагнитных волн не может измениться (в силу закона сохранения полного импульса системы), то из этого следует, что электромагнитная волна также обладает импульсом. Существование И. э. п. впервые было экспериментально обнаружено в опытах подавлению света(П. Н. Лебедев, 1899).

Из классической теории электромагнитного поля — Максвелла уравнений — следует, что И. э. п. распределён в пространстве с объёмной плотностью    — в системе СГС (Гаусса), или    — в системе СИ, где [ЕН] — векторное произведение напряжённостей электрического Е и магнитного Н полей, численно равное EH sin a, a — угол междуE иH, с = 3×10¹⁰см/сек — скорость света в вакууме. Таким образом, вектор плотности И. э. п. g перпендикулярен Е и Н и направлен в сторону поступательного движения правого буравчика, рукоятка которого вращается в направлении от ЕкH.

В квантовой теории электромагнитного поля (квантовой электродинамике) носителем энергии и импульса поля являются кванты этого поля — фотоны. Фотон частоты n обладает энергией hn и импульсом h n/c, где h — Планка постоянная. Существование импульса у фотона проявляется во многих явлениях. Например, обмен импульсом между электромагнитным полем и частицей имеет место в Комптона эффекте (упругом рассеянии фотонов на электронах).

Билет 38

ТЕОРИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ ДЖЕЙМСА МАКСВЕЛЛА

Эта теория была создана Джеймсом Максвелом в 1865г., согласно ей:

«Любое изменение со временем магнитного поля приводит к возникновению изменяющегося электрического поля, а всякое изменение со временем электрического поля порождает изменяющееся магнитное поле. Если электрические заряды движутся с ускорением, то создаваемое ими электрическое поле периодически меняется и само создает в пространстве переменное магнитное поле и т.д.»

Получается, что основными действующими лицами здесь являются МАГНИТ и ЭЛЕКТРИЧЕСКИЙ ЗАРЯД.

«Электрическое поле существует всегда вокруг электрического заряда, в любой системе отсчета, магнитное – в той, относительно которой электрические заряды движутся,  электромагнитное – в системе отсчета, относительно которой электрические заряды движутся с ускорением»

Уравнения Максвелла для электромагнитного поля

Объяснение и создание математической модели физического процесса или явления далеко не всегда можно решить «в лоб». Зачастую, приходиться вводить к основным понятиям некоторые дополнительные аргументы, чтобы показать функцию во всей красе. 

Один из ярких примеров такого подхода может служить введение Максвеллом понятия тока смещения. Это позволило ему завершить созданную им теорию электромагнитного поля, которая позволила не только объяснить электрические и магнитные явления, но и предсказать новые, существование которых было впоследствии подтверждено.

В основе теории Максвелла лежат четыре уравнения.  1. Электрическое поле может быть как потенциальным (EQ), так и вихревым (EB), поэтому напряженность суммарного поля E = EQ + EB.  Так как циркуляция вектора EQ равна нулю   а циркуляция вектора EB определяется выражением то циркуляция вектора напряженности суммарного поля

  [1]

Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.

2. Обобщенная теорема о циркуляции вектора H 

Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.

3. Теорема Гаусса для поля D  Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью ρ, то формула [3] запишется в виде 4. Теорема Гаусса для поля B Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):   

где ε0 и μ0 – соответственно электрическая и магнитная постоянная, ε и μ – соответственно диэлектрическая и магнитная проницаемость, γ – удельная проводимость вещества.

Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями.

Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных. Для стационарных полей (E=const и B=const) уравнения Максвелла примут вид:

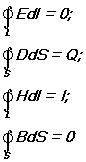
т.е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного – только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрические и магнитные поля. Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса

можно представить полную систему уравнений Максвелла в дифференциальной форме (характеризующих поле в каждой точке пространства):

 

Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла – интегральная и дифференциальная – эквивалентны. Однако если имеются поверхности разрыва (поверхности, на которых свойства среды или полей меняются скачкообразно), то интегральная форма уравнений является более общей.

Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняю граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия

 

Первое и последнее уравнение отвечают случаям, когда на границе раздела двух сред нет ни свободных зарядов, ни токов проводимости.

Уравнения Максвелла – наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т.е. электрическое и магнитное поля неразрывно связаны друг с другом – они образуют единое электромагнитное поле.

Билет 37

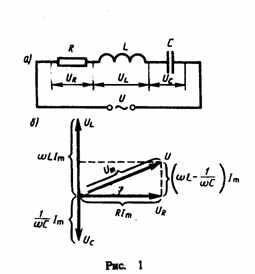
Найдем мгновенное значение мощности переменного тока, которое равно произведению мгновенных значений напряжения и силы тока:    где U(t)=U_mcosωt, I(t)=I_mcos(ωt-φ) . Раскрыв cos(ωt-φ), найдем    На практике, представляет интерес не мгновенное значение мощности, а ее среднее значение за период колебания. Поскольку <cos²ωt>= 1/2, <sinωtcosωt> = 0, то   (1)  Из векторной диаграммы (рис. 1) следует, что U_mсosφ = RI_m. Значит    Такую же мощность дает постоянный ток   . 

Величины    имеют названия соответственно действующими (или эффективными) значениями тока и напряжения. Все вольтметры и амперметры градуируются по действующим значениям тока и напряжения.  Зная действующие значения тока и напряжения, выражение средней мощности (1) запишем как   (2)  где множитель соsφ называется коэффициентом мощности.  Из выражении (2) видно, что мощность, которая выделяется в цепи переменного тока, в общем случае зависит не только от силы тока и напряжения, но также и от сдвига фаз между ними. Если реактивное сопротивление в цепи отсутствует, то cosφ=1 и P=IU. Если в цепи имеется только реактивное сопротивление (R=0), то cosφ=0 и средняя мощность равна нулю, какими бы большими ни были ток и напряжение. Если cosφ существенно меньшие единицы, то для передачи заданной мощности при данном напряжении генератора нужно повысить силу тока I, что приведет либо к выделению теплоты Джоуля-Ленца, либо в этом случае нужно увеличение сечения проводов, что повышает стоимость линий электропередачи. Поэтому на практике всегда стремятся повысить значение соsφ, наименьшее допустимое значение которого для промышленных установок равно примерно 0,85.