Первое правило

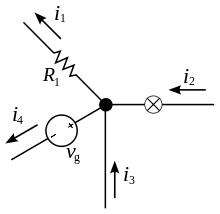
Сколько тока втекает в узел, столько из него и вытекает. i₂ + i₃ = i₁ + i₄

Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.

Второе правило

Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

для постоянных напряжений 

для переменных напряжений 

Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.

Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).

Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.

Билет № 15

Закон Джо́уля — Ле́нца — физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцем

В словесной формулировке звучит следующим образом^[2]

Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину напряженности электрического поля

Математически может быть выражен в следующей форме:

где   — мощность выделения тепла в единице объёма,   — плотность электрического тока,   — напряжённость электрического поля, σ — проводимость среды.

Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах^[3]:

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивления участка

В математической форме этот закон имеет вид

где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t₁ до t₂. В случае постоянных силы тока и сопротивления:

Билет № 16

Классическая теория электропроводности металлов (теория Друде-Лоренца). Для выяснения природы носителей тока был поставлен ряд опытов. Рикке в 1901 году взял три цилиндра - два медных и один алюминиевый-с хорошо отшлифованными торцами, взвесил их и сложил последовательно медь-алюминий –медь. Через такой составной проводник в течение года непрерывно пропускался постоянный ток. За год через этот проводник прошел заряд порядка 10³ Кл. Исследования цилиндров показало, что пропускание тока не повлияло на вес цилиндров, и не было обнаружено проникновение одного металла в другой на торцах цилиндров. Таким образом, опыты показывали, что перенос заряда в металле осуществляется не атомами. Можно было предположить, что заряд переносится электронами. Но чтобы это доказать, надо было определить значение удельного заряда носителей тока (удельный заряд- это отношение заряда к массе частицы). Если в металлах имеются свободные заряженные частицы, то при движении проводника частицы движутся вместе с ним. Если проводник резко затормозить, то свободные частицы некоторое время должны двигаться по инерции, в результате чего в проводнике возникнет импульс тока и будет перенесен некоторый заряд. Пусть проводник движется со скоростью v₀. Начнем тормозить проводник с ускорением  . Свободные заряды продолжают двигаться по инерции и приобретают относительно проводника ускорение  . Такое же ускорение можно сообщить носителям заряда, если их поместить в электрическое поле напряженностью Е.  . Получить такое поле можно, приложив к концам проводника разность потенциалов  , где l – длина проводника. По проводнику потечет ток:  , а, следовательно, за время dt через сечение проводника пройдет заряд  . Таким образом, заряд, прошедший за все время торможения, равен . (1) Измерив  , можно определить удельный заряд носителей тока  , а направление импульса тока даст знак носителей. Первый качественный опыт был сделан в 1913 году С.Л. Мандельштамом и Н.Д. Папалекси. Они привели катушку, к концам которой был подключен телефон, в быстрые крутильные колебания, и резко останавливали. В этот момент в трубке телефона был слышен звук, обусловленный импульсом тока.  Количественный опыт был поставлен в 1916 году Р. Толменом и Б. Стьюартом. Катушка приводилась в быстрое вращение, а затем резко тормозилась. Гальванометром измерялся заряд, прошедший в цепи за время торможения. И по формуле (1) вычислялся удельный заряд носителей тока. Он оказался близким по значению к удельному заряду электрона. Таким образом, ток в металле обусловлен свободными электронами. При образовании кристаллической решетки слабо связанные валентные электроны отщепляются от атомов, и поступают в собственность всего куска металла. Концентрация свободных носителей заряда порядка  . Исходя из представления о свободных электронах, П. Друде и Х. Лоренц создали теорию электропроводности металлов. Согласно этой теории свободные электроны ведут себя как молекулы идеального газа. В промежутках между столкновениями они движутся свободно, пробегая некоторый путь  . Столкновения электронов осуществляется преимущественно с ионами решетки, и это приводит к тепловому равновесию между электронным газом и кристаллической решеткой. Среднюю скорость теплового движения электронов можно произвести по формуле:  . При   эта скорость порядка 10⁵ м/с. При включении поля на хаотическое движение частиц накладывается упорядоченное движение с некоторой средней скоростью  . Ее можно оценить из выражения . (2) Предельно допустимая плотность тока для медных проводников  10⁷ А/м², а концентрация электронов  . Заряд электрона равен 1.6·10^-19 Кл. Подставляя все эти значения в формулу (2) получаем, что средняя скорость направленного движения частиц равна  . Т.е. даже при очень больших плотностях тока средняя скорость теплового движения много больше средней скорости направленного движения, вызванного электрическим полем. Получим основные законы электропроводности на основе теории Друде- Лоренца. Согласно этой теории при соударении электрона с ионом кристаллической решетки приобретенная электроном дополнительная энергия полностью передается иону, и, следовательно, скорость электрона становится равной нулю. Под действием поля электроны ускоряются и приобретают ускорение, равное  . За время свободного пробега  скорость электрона увеличивается до  . Считая, что скорость всех электронов одинакова, можно записать, что время свободного пробега электрона равно  , где u практически равна скорости хаотического движения электронов.  . Скорость изменяется линейно за время свободного пробега, поэтому средняя скорость упорядоченного движения электронов равна  . Плотность тока:  . (3) Таким образом, плотность тока оказалась пропорциональной напряженности. Выражение (3) можно записать в виде:  (4) Полученная формула выражает закон Ома в дифференциальной форме. Здесь   - коэффициент пропорциональности, проводимость металла.  Если бы не было столкновений между электронами и ионами решетки, то проводимость была бы бесконечной. Определим температурную зависимость проводимости. Концентрация электронов и длина свободного пробега не должны зависеть от температуры. От температуры зависит только средняя скорость теплового движения.  . Следовательно, проводимость обратно пропорциональна корню из Т, а сопротивление возрастает как корень из Т. Эксперимент показывает, что сопротивление в широком интервале температур пропорционально температуре, и только при низких температура турах  . Таким образом, теория проводимости металлов Друде-Лоренца, приводя к закону Ома, не может объяснить температурной зависимости сопротивления. Объяснение может дать только квантовая теория. У ряда металлов при низких температурах наблюдается явление сверхпроводимости: при понижении температуры, начиная с некоторой температуры, называемой критической, сопротивление становится равным нулю. Сверхпроводимость может нарушаться магнитным полем. Явление сверхпроводимости – это чисто квантовое явление, и его мы будем рассматривать в следующем семестре. Получим закон Джоуля-Ленца на основании теории Друде-Лоренца. К концу свободного пробега электрон приобретает кинетическую энергию: , (5) Здесь учтено, что для электрона иметь скорость v и u статистически независимые события, а средняя скорость теплового движения  . Последнее слагаемое в формуле (5)  - средняя кинетическая энергия теплового движения. Т.о. в присутствии поля, электрон приобретает дополнительную энергию  . Столкнувшись с ионом, электрон полностью передает эту энергию кристаллической решетке. Эта энергия идет на увеличение внутренней энергии решетки, т.е. на нагревание. Каждый электрон за секунду претерпевает   столкновений. Следовательно, в единице объема за единицу времени должно выделится тепло:  . Коэффициент при   совпадает с  . Т.о.  - это и есть закон Джоуля-Ленца. ^ Закон Видемана–Франца. Видеман и Франц установили связь между коэффициентом теплопроводности и электропроводности для всех металлов. Теплопроводность металлов, как показывает опыт, значительно выше теплопроводности диэлектриков. Из этого следует, что теплопроводность в металлах осуществляется в основном не кристаллической решеткой, а свободными электронами. Поэтому, рассматривая электроны, как одноатомный газ, используем формулу для коэффициента теплопроводности газов:  . Удельная теплоемкость одноатомного газа:  . Отношение коэффициента теплопроводности к коэффициенту электропроводности:  . Т.о. отношение коэффициента теплопроводности к коэффициенту электропроводности пропорционально температуре. Это соотношение хорошо согласуется с экспериментальными данными. Но уточненные Лоренцем расчеты получили другое соотношение между  и , которое хуже согласуется с экспериментальными данными. Т.е. классическая теория дает только качественное соответствие закона Видемана –Франца. Теплоемкость металла можно представить как теплоемкость решетки и теплоемкость электронного газа. Каждый атом колеблется около своего положения равновесия и имеет три степени свободы. Энергия, приходящаяся на каждую колебательную степень свободы  . Поэтому молярная теплоемкость решетки:  . Теплоемкость электронного газа:  . Следовательно, полная теплоемкость металла  . У диэлектриков теплоемкость обусловлена только решеткой. Т.е. теплоемкость металла должна быть в 1.5 раза больше теплоемкости диэлектрика, а эксперимент показывает, что их теплоемкости почти одинаковы. Объяснение всех несоответствий классической теории электропроводности металлов с экспериментом объясняется только квантовой теорией металлов.

Билет №17

Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения^[1], магнитная составляющая электромагнитного поля^[2].

Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).

Кроме этого, оно появляется при наличии изменяющегося во времени электрического поля.

Основной силовой характеристикой магнитного поля является вектор магнитной индукции   (вектор индукции магнитного поля)^[3][4]. С математической точки зрения   — векторное поле, определяющее и конкретизирующее физическое понятие магнитного поля. Нередко вектор магнитной индукции называется для краткости просто магнитным полем (хотя, наверное, это не самое строгое употребление термина).

Ещё одной фундаментальной характеристикой магнитного поля (альтернативной магнитной индукции и тесно с ней взаимосвязанной, практически равной ей по физическому значению) является векторный потенциал.

• Нередко в литературе в качестве основной характеристики магнитного поля в вакууме (то есть в отсутствие магнитной среды) выбирают не вектор магнитной индукции  а вектор напряжённости магнитного поля  , что формально можно сделать, так как в вакууме эти два вектора совпадают^[5]; однако в магнитной среде вектор   не несет уже того же физического смысла^[6], являясь важной, но всё же вспомогательной величиной. Поэтому при формальной эквивалентности обоих подходов для вакуума, с систематической точки зрения следует считать основной характеристикой магнитного поля именно 

Магнитное поле можно назвать особым видом материи^[7], посредством которого осуществляется взаимодействие между движущимися заряженными частицами или телами, обладающими магнитным моментом.

Магнитные поля являются необходимым (в контексте специальной теории относительности) следствием существования электрических полей.

Вместе, магнитное и электрическое поля образуют электромагнитное поле, проявлениями которого являются, в частности, свет и все другие электромагнитные волны.

Принцип суперпозиции магнитных полей: если магнитное поле создано несколькими проводниками с токами, то вектор магнитной индукции в какой-либо точке этого поля равен векторной сумме магнитных индукций, созданных в этой точке каждым током в отдельности:

Линии магнитной индукции - линии, касательные к которым направлены также как и вектор магнитной индукции в данной точке поля. Магнитные поля, так же как и электрические, можно изображать графически при помощи линий магнитной индукции. Через каждую точку магнитного поля можно провести линию индукции. Так как индукция поля в любой точке имеет определённое направление, то и направление линии индукции в каждой точке данного поля может быть только единственным, а значит, линии магнитного поля, так же как и электрического поля, линии индукции магнитного поля прочерчивают с такой густотой, чтобы число линий, пересекающих единицу поверхности, перпендикулярной к ним, было равно (или пропорционально) индукции магнитного поля в данном месте. Поэтому, изображая линии индукции, можно наглядно представить, как меняется в пространстве индукция, а следовательно, и напряжённость магнитного поля по модулю и направлению.

Пра́вило бура́вчика (пра́вило винта́), или пра́вило правой руки — варианты мнемонического правила для определения направления векторного произведения и тесно связанного с этим выбора правого базиса^[1] в трехмерном пространстве, соглашения о положительной ориентации базиса в нем, и соответственно — знака любого аксиального вектора, определяемого через ориентацию базиса.

Билет №18

Закон Био́—Савара—Лапла́са — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током.

Согласно закону Био-Савара-Лапласа, индукция магнитного поля, создаваемого элементом тока dl на расстоянии r от него есть

,

где  α – угол между элементом тока  и радиус-вектором  , проведенным из этого элемента в точку наблюдения; r - расстояние от элемента тока до точки наблюдения.

В нашем случае α = π/2, sinα = 1;  , где а – расстояние, отсчитываемое от центра витка до рассматриваемой точки на оси витка. Векторы   образуют в этой точке конус с углом раствора при вершине 2  = π - 2β, где β – угол между отрезками а и r.

Из соображений симметрии ясно, что результирующее магнитное поле на оси витка будет направлено вдоль этой оси, то есть вклад в него дают только те составляющие, которые параллельны оси витка:

.

Результирующую величину индукции магнитного поля B на оси витка получим, проинтегрировав это выражение по длине контура от 0 до 2πR:

или, подставив значение r:

.

В частности, при а = 0 находим индукцию магнитного поля в центре кругового витка с током:

Этой формуле можно придать другой вид, воспользовавшись определением магнитного момента витка с током:

.

Последнюю формулу можно записать в векторном виде (см. рис.9.1):

.

    Рассмотрим магнитное поле прямого тока (рис. 1.6).

Рис. 1.6

      Все векторы    от произвольных элементарных участков    имеют одинаковое направление. Поэтому сложение векторов можно заменить сложением модулей.

      Пусть точка, в которой определяется магнитное поле, находится на расстоянии b от провода. Из рисунка 1.6 видно, что:

   Для бесконечно длинного проводника    а  , тогда

      или, что удобнее для расчетов,

Билет №19

Циркуляцией вектора магнитной индукции В по заданному контуру называется интеграл

закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора магнитной индукции) где n – число проводников с токами, охватываемых контуром L произвольной формы.

1. Существует принципиальное различие между циркуляцией вектора напряженности электрического поля Е и циркуляцией вектора магнитной индукции В: циркуляция Е почти всегда равна нулю, циркуляция В не равна нулюи это означает, что магнитное поле является вихревым.

2. Теорема о циркуляции вектора магнитной индукции играет в магнитостатике такую же роль, как и теорема Остроградского-Гаусса в электростатике.

1. Рассчитаем, применяя теорему о циркуляции, индукцию магнитного поля внутри соленоида. Рассмотрим соленоид длиной l, имеющий N витков, по которому течет ток (рис. 175). Длину соленоида считаем во много раз больше, чем диаметр его витков, т. е. рассматриваемый соленоид бесконечно длинный. Экспериментальное изучение магнитного поля соленоида (см. рис. 162, б) показывает, что внутри соленоида поле является однородным, вне соленоида — неоднородным и очень слабым.

2. На рис. 175 представлены линии магнитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем меньше магнитная индукция вне его. Поэтому приближенно можно считать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а полем вне соленоида можно пренебречь.

3. Для нахождения магнитной индукции В выберем замкнутый прямоугольный кон­тур ABCDA, как показано на рис. 175. Циркуляция вектора В по замкнутому контуру ABCDA, охватывающему все N витков, согласно (118.1), равна

4. 

5. Интеграл по ABCDA можно представить в виде четырех интегралов: по АВ, ВС, CD и DA. На участках АВ и CD контур перпендикулярен линиям магнитной индукции и B_l=0. На участке вне соленоида B=0. На участке DA циркуляция вектора В равна Вl (контур совпадает с линией магнитной индукции); следовательно,

6.                                                      (119.1)

7. Из (119.1) приходим к выражению для магнитной индукции поля внутри соленоида (в вакууме):

8.                                                                   (119.2)

9. Получили, что поле внутри соленоида однородно (краевыми эффектами в областях, прилегающих к торцам соленоида, при расчетах пренебрегают). Однако отметим, что вывод этой формулы не совсем корректен (линии магнитной индукции замкнуты, и интеграл по внешнему участку магнитного поля строго нулю не равен). Корректно рассчитать поле внутри соленоида можно, применяя закон Био - Савара - Лапласа; в результате получается та же формула (119.2).

10. Важное значение для практики имеет также магнитное поле тороида — кольцевой катушки, витки которой намотаны на сердечник, имеющий форму тора (рис. 176). Магнитное поле, как показывает опыт, сосредоточено внутри тороида, вне его поле отсутствует.

11. 

12. Линии магнитной индукции в данном случае, как следует из соображений симмет­рии, есть окружности, центры которых расположены по оси тороида. В качестве контура выберем одну такую окружность радиуса r. Тогда, по теореме о циркуляции (118.1), B×2pr=m₀NI, откуда следует, что магнитная индукция внутри тороида (в вакууме)

13. 

14. где N — число витков тороида.

15. Если контур проходит вне тороида, то токов он не охватывает и B×2pr=0. Это означает, что поле вне тороида отсутствует (что показывает и опыт).