4 Этап

На множестве  введем бинарную операцию  - «состоять из» следующим образом: отрезок с состоит из отрезков a и b, если он является их объединением с точки зрения точечных множеств, причем отрезки a и b лежат на одной прямой и не имеют общих внутренних точек, но имеют одну общую граничную точку.

П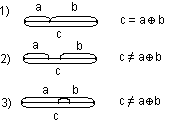 римеры:

5 Этап

Каждому классу эквивалентности поставим в соответствие единственный образ - положительную скалярную величину «длина». Обозначим l(a) – длина отрезка а.

Каждому отрезку данного класса будет соответствовать величина «длина» одна и та же.

Из пяти приведенных этапов следует вывод:

1. Каждый отрезок имеет длину.

2. Равные отрезки имеют равные длины.

Так как длина отрезка - положительная скалярная величина, то она подчиняется аксиомам положительных скалярных величин.

Аксиома 1

Длины любых двух отрезков a и b можно сравнить (наложением). В результате получается одно из трех утверждений:

1) l(a)=l(b)

2) l(a)<l(b)

3) l(a)>l(b), где l(a)- длина отрезка a, l(b)- длина отрезка b.

Длина отрезка а меньше длины отрезка b, если при наложении отрезок а умещается в отрезке b всеми своими точками и обратное неверно.

Аксиома 2

Длины любых отрезков можно складывать. В результате получим длину нового отрезка.

Если l(b)-длина отрезка b, l(c)-длина отрезка c, l(a) – длина отрезка a, такого, что

a= b  c. Тогда l(b) + l(c) = l(a) .

Аксиома 3

Из длины большего отрезка можно вычесть длину меньшего отрезка. В результате получим длину нового отрезка.

l(a) - l(b) = l(c), т.е. получим длину отрезка с, такого, что a= b  c.

Аксиома 4

Длину любого отрезка можно умножить на положительное действительное число. В результате получим длину нового отрезка.

l(a) 4 = l(c)

Аксиома 5

Длину одного отрезка можно разделить на длину другого отрезка. В результате получим положительное действительное число.

l(c): l(a) = 4

1.2. Процесс измерения длины отрезка

Допустим, нужно измерить длину отрезка а.

Выберем произвольный отрезок е и назовем его единичным. Отрезок е, как и все остальные, имеет длину. Длине единичного отрезка е поставим в соответствие положительное действительное число 1.

Записывают: l(e) 1 или m_е(е)=1 (мера длины отрезка е при единице измерения е равна 1).

Узнаем, из скольких единичных отрезков е состоит отрезок а. Для этого разделим длину отрезка а на длину отрезка е. При этом могут получиться различные случаи.

Случай 1

Отрезок а состоит из целого числа отрезков е.

Тогда m_е(а) N. Можно записать: m_е(а) = 5 или l(a) 5. Процесс измерения закончен.

Случай 2

Отрезок а не состоит из целого числа отрезков е.

Тогда m_е(а)N. Получили, что длина отрезка а больше длины отрезка, состоящего из 5 отрезков е, и меньше длины отрезка, состоящего из 6 отрезков е. Можно оценить приближенно по недостатку и по избытку: 5 < m_е(a) < 6.

В этом случае необходимо перейти к новой единице измерения е₁, которая представляет собой десятую долю отрезка е.

е₁  е₁  ...  е₁ = е е₁ = е

10 слагаемых

l(e₁) m_е(e₁)=

Подсчитаем, из скольких отрезков е₁ состоит отрезок а. Опять могут получиться различные случаи.

Случай 2.1

Отрезок а состоит из целого числа отрезков е₁. Тогда m_е1(а)N. Например, m_е1(а)= 53. Перейдем к прежней единице измерения, используя свойство мультипликативности меры:

m_е(а)= m_е1(a)  m_е(e₁)= 53  = 5,3.

Процесс измерения закончен.

Случай 2.2

Отрезок а не состоит из целого числа отрезков е₁. Например, 53<m_е1(a)<54 или, переходя к прежней единице измерения: 5,3<m_е(a)< 5,4.

П роцесс измерения не закончен, поэтому необходимо вновь ввести новую единицу измерения е₂, которая составляет десятую долю мерки е₁ или сотую долю мерки е. е₂  е₂  е₂  ...  е₂ = е е₂ = е 100 слагаемых

l(e₂) m_е(e₂)=

Подсчитаем, из скольких отрезков е₂ состоит отрезок а. Опять могут получиться различные случаи.

Случай 2.2.1

Отрезок а состоит из целого числа отрезков е₂. Тогда m_е2(а)N. Например, m_е2(а)= 534. Перейдем к прежней единице измерения, используя свойство мультипликативности меры:

m_е(а)= m_е2(a) m_е(e₂)= 534  = 5,34.

Процесс измерения закончен.

Случай 2.2.2

Отрезок а не состоит из целого числа отрезков е₂. Например, 534<m_е2(a)<535 или, переходя к прежней единице измерения: 5,34<m_е(a)< 5,35.

Процесс измерения не закончен, поэтому необходимо вновь ввести новую единицу измерения е₃ , которая составляет десятую долю мерки е₂ или сотую долю мерки е₁ или тысячную долю мерки е. Далее продолжаем процесс измерения по аналогии.

Таким образом, в общем случае:

1. Если отрезок а состоит из целого числа отрезков е, то мера длины отрезка а при единице измерения е выражается натуральным числом. Например, m_е(a)=5.

Если этого не произошло, то перейти к новой единице и продолжать процесс измерения.

2. Если отрезок а состоит из целого числа некоторой 10ⁿ - доли единичного отрезка е, то мера длины отрезка а выражается конечной десятичной дробью, которую определим с помощью свойства мультипликативности меры. Например, m_е(a)=5,34.

3. Если отрезок а не состоит из целого числа ни каких 10ⁿ - долей единичного отрезка е, то процесс измерения бесконечен, и мера длины отрезка а при единице измерения е выражается бесконечной десятичной дробью. Например, m_е(a)=5,345276... .