17. Закон Джоуля-Ленца. Работа и мощность тока.

Рассмотрим однородный проводник, к концам которого приложено напряжение U.

За "время dt через сечение проводника переносится заряд dq=Idt. Так как ток представляет собой перемещение заряда dq под действием электрического поля, то работа тока равна:

dA = Udq = IUdt

Если сопротивление проводника R, то, используя закон Ома получаем, что работа тока:

Из формул (1) и (2) следует, что мощность тока:

Если ток проходит по неподвижному металлическому проводнику, то вся работа тока идет на его нагревание и, по закону сохранения энергии: dQ = dA.

Таким образом, используя выражения (1), (2) и (3), получим закон Джоуля - Ленца:

Количество теплоты, выделяющееся за единицу времени в единице объема, называется удельной тепловой мощностью тока. Она равна . Используя дифференциальную форму закона Ома (j=Е) и соотношение =1/, получим: . Формулы (4) и (5) являются обобщенным выражением закона Джоуля—Ленца в дифференциальной форме, пригодным для любого проводника.

18. Правила Кирхгофа.

Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:

Например, для рисунка (1) первое правило Кирхгофа запишется так:

П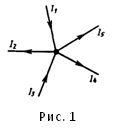 ервое правило Кирхгофа вытекает из закона сохранения электрического заряда.

Действительно, в случае установившегося постоянного тока ни в одной точке провод­ника и ни на одном его участке не должны накапливаться электрические заряды. В противном случае токи не могли бы оставаться постоянными.

Второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов I_i на сопротивления R_i соответствующих участков этого контура равна алгебраической сумме ЭДС, встречающихся в этом контуре:

Источники тока считаются положительными, если они создают ток, направленный в сторону обхода контура. Применяя к участкам закон Ома, можно записать:

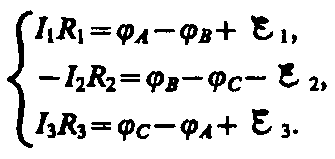
Складывая почленно эти уравнения, получим второе правило Кирхгофа:

При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо:

1. Выбрать произвольное направление токов на всех участках цепи; действительное направление токов определяется при решении задачи: если искомый ток получится положительным, то его направление было выбрано правильно, отрицательным — его истинное направление противоположно выбранному.

2. Выбрать направление обхода контура и строго его придерживаться; произведе­ние IR положительно, если ток на данном участке совпадает с направлением обхода, и, наоборот, ЭДС, действующие по выбранному направлению обхода, считаются поло­жительными, против — отрицательными.

3. Составить столько уравнений, чтобы их число было равно числу искомых величин (в систему уравнений должны входить все сопротивления и ЭДС рассматрива­емой цепи); каждый рассматриваемый контур должен содержать хотя бы один элемент, не содержащийся в предыдущих контурах, иначе получатся уравнения, являющиеся простой комбинацией уже составленных.

19. Магнитная индукция. Линии магнитной индукции. Закон Био-Савара-Лапласа.

Отношение М_max/р_m (М_max — максимальный вращающий момент) для всех контуров одно и то же и поэтому может служить характеристикой магнитного поля, называемой магнитной индукцией: B = M_max/p_m.

Линии магнитной индукции – линии касательные к которым в каждой точке совпадают с направлением вектора В. Направление задаётся правилом правого винта. Линии всегда замкнуты.

Закон Био — Савара — Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А индукцию поля dB, записывается в виде где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r—радиус-вектор, проведанный из элемента dl проводника в точку А поля, r — модуль радиуса-вектора r.

Применение закона Био-Савара -Лапласа. Закон Био-Савара-Лапласа для проводника с током I, элемент dl которого создает в некоторой точке A индукцию поля записывается в виде: . Направление определяется правилом правого винта. М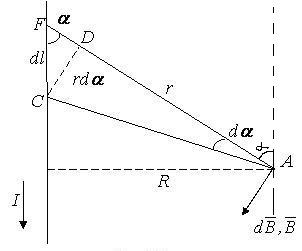 одуль вектора равен .

Магнитное поле прямого тока: В произвольной точке A, удаленной от оси проводника на расстояние R, векторы db от всех элементов тока имеют одинаковое направление, перпендикулярное к плоскости чертежа. В качестве постоянной интегрирования выберем угол и выразим все величины через него: r = , dl = . Подставим эти выражения в ,получаем что магнитная индукция создаваемая одним элементом проводника, равна . Т.к. угол для всех элементов изменяется в пределах от 0 до , то: или Магнитное поле движущегося заряда:

Каждый проводник с током создает в окружающем пространстве магнитное поле. В результате обобщения опытных данных был установлен закон, определяющий поле точечного заряда Q , движущегося с постоянной скоростью : .

Модуль магнитной индукции равен .