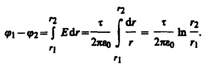5. Циркуляция вектора напряжённости электростатического поля. Работа электростатического поля. Потенциал – энергетическая характеристика электростатического поля.

Циркуляция вектора напряженности электростатического поля по любому замкнутому контуру равна нулю. Это утверждение выражает теорему о циркуляции электростатического поля. При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Потенциал – энергетическая характеристика электрического поля равен отношению потенциальной энергии заряда в поле к этому заряду.

6. Напряжённость – градиент потенциала. Эквипотенциальные поверхности.

Напряженность как градиент потенциала различают две характеристики электростатического поля: силовую (напряженность) и энергетическую (потенциал).

Напряженность и потенциал - различные характеристики одной и той же точки поля; следовательно, между ними должна существовать связь.

Рассматривая две точки с координатами (x, y, z) и (x+dx, y, z), между которыми перемещается заряд, можно сделать вывод, что напряженность как градиент потенциала имеет формулу:

Величина, характеризующая быстроту изменения потенциала в направлении силовой линии, называется градиентом потенциала

Отсюда следует, что вектор напряженности Е численно равен градиенту потенциала и направлен в сторону убывания потенциала. Связь между напряженностью и потенциалом позволяет по известной напряженности поля найти разность потенциалов между двумя произвольными точками этого поля.

Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью. Между двумя любыми точками на эквипотенциальной поверхности разность потенциалов равна нулю, поэтому работа сил электрического поля при любом перемещении заряда по эквипотенциальной поверхности равна нулю.

7. Вычисление разности потенциалов по напряжённости поля для бесконечной плоскости, параллельных плоскостей; для сферической поверхности, объёмно заряженного шара, бесконечного цилиндра.

Установленная связь между напряженностью поля и потенциалом позволяет по известной напряженности поля найти разность потенциалов между двумя произвольными точками этого поля.

1. Поле равномерно заряженной бесконечной плоскости определяется формулой (82.1): E=s/(2e₀), где s — поверхностная плотность заряда. Разность потенциалов между точками, лежащими на расстояниях x₁ и х₂ от плоскости, равна (используем формулу (85.1))

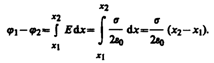
2. Поле двух бесконечных параллельных разноименно заряженных плоскостей определяется формулой (82.2); Е=s/e₀, где s — поверхностная плотность заряда. Разность потенциалов между плоскостями, расстояние между которыми равно d (см. формулу (85.1)), равна

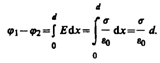
3. Поле равномерно заряженной сферической поверхности радиуса R с общим зарядом Q вне сферы

(r> R) вычисляется по (82.3):   Разность потенциалов между двумя точками, лежащими на расстояниях r₁ и r₂ от центра сферы (r₁ >R, r₂>R, r₂>r₁), равна

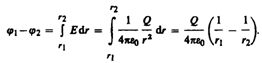Если принять r₁=r и r₂=¥, то потенциал поля вне сферической поверхности, согласно формуле (86.2), задается выражением

(ср. с формулой (84.5)). Внутри сферической поверхности потенциал всюду одинаков и равен

График зависимости j от r приведен на рис. 134.

4. Поле объемно заряженного шара радиуса R с общим зарядом Q вне шара (r>R) вычисляется по формуле (82.3), поэтому разность потенциалов между двумя точками, лежащими на расстояниях r₁ и r₂ от центра шара (r₁ > R, r₂ > R, r₂ > r₁), определяется формулой (86.2). В любой точке, лежащей внутри шара на расстоянии r' от его центра (r'<R), напряженность определяется выражением (82.4):   Следовательно, разность потенциалов между двумя точками, лежащими на расстояниях   и   от центра шара ( <R,  <R,  > ), равна

5. Поле равномерно заряженного бесконечного цилиндра радиуса R, заряженного с линейной плотностью t, вне цилиндра (r>R) определяется формулой (82.5):   Следовательно, разность потенциалов между двумя точками, лежащими на расстояниях r₁ м r₂ от оси заряженного цилиндра (r₁>R, r₂>R, r₂>r₁), равна