
Теоретическая механика. Теория, задания и примеры решения задач (Б.Е.Ермаков)
.pdf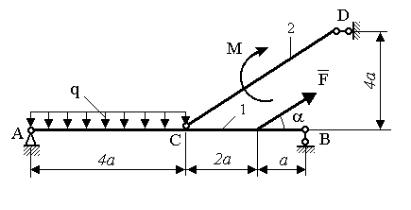
60
расчета. При первом способе (способ “заморозки” соединительных шарниров) составляют уравнения равновесия для заданных сил и реакции внешних связей, а затем записывают уравнения равновесия для одного из тел конструкции. При втором способе всю конструкцию расчленяют на отдельные тела и составляют уравнения равновесия отдельно для каждого тела. В данной задаче следует использовать только второй способ.
Пример решения задачи
Дано: схема конструкции (рис. 39); F = 10 кН; M = 6 кНм; q = 2 кН/м; a = 1 м.
Определить реакции опор A, B и D конструкции.
Рис. 39
Решение
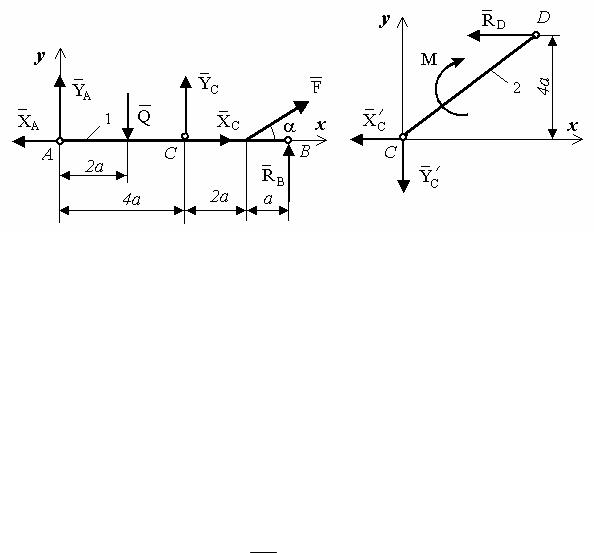
Рассмотрим отдельно тела 1 и 2 с приложенными к ним активными силами и реакциями связей (рис. 40 – 41). Равномерно распределенную нагрузку заменяем одной силой Q = 4qa.
Для системы сил рис. 40 составляем три уравнения равновесия
(первая форма). |
|
|
ΣFkx = 0; |
F cosα + XC - XA = 0; |
(1) |
ΣFky = 0; |
F sinα + YA – Q + YC + RB = 0; |
(2) |
ΣmA(Fk) = 0; -Q 2a + YC 4a + F sinα 6a + RB 7a = 0. |
(3) |
|
61
|
|
|
|
Рис. 40 |
|
Рис. 41 |
|
Для системы сил рис. 41 составим еще три уравнения |
|||
ΣFkx = 0; |
-RD - XC′ = 0; |
(4) |
|
ΣFky = 0; |
-YC′ = 0; |
(5) |
|
ΣmС(Fk) = 0; |
RD 4a – M = 0. |
(6) |
|
При равенстве внутренних сил XC = XC′ и YC = YC′ из уравнения (6) находим
RD = 4Ma = 64 =1,5кН.
Уравнения (4) и (5) определяют:
YC = YC′ = 0; XC = XC′ = -RD = -1,5 кН.
Из уравнения (3) находим
RB = 1/7 (2Q – 6F sinα) = 1/7 (2 4 2 - 6 10 sin300) = -2 кН.
Уравнения (1) и (2) определяют реакции XA и YA.
XA = F cosα + XC = 10 cos300 – 1,5 = 7,16 кН; YA = Q - F sinα - RB = 4 2 - 10 sin300 – (-2) = 5 кН;
XA = 7,16 кН; YA = 5 кН; RB = -2 кН; RD = 1,5 кН.
62
Проверка. Для всей конструкции запишем одно уравнение статики ΣFkx = 0.
F cosα - XA - RD = 0; F cosα = XA + RD;
10 cos300 = 7,16 + 1,5; |
8,66 = 8,66. |
Реакции опор найдены верно.
63
Задача С.6. Плоская составная конструкция рамы
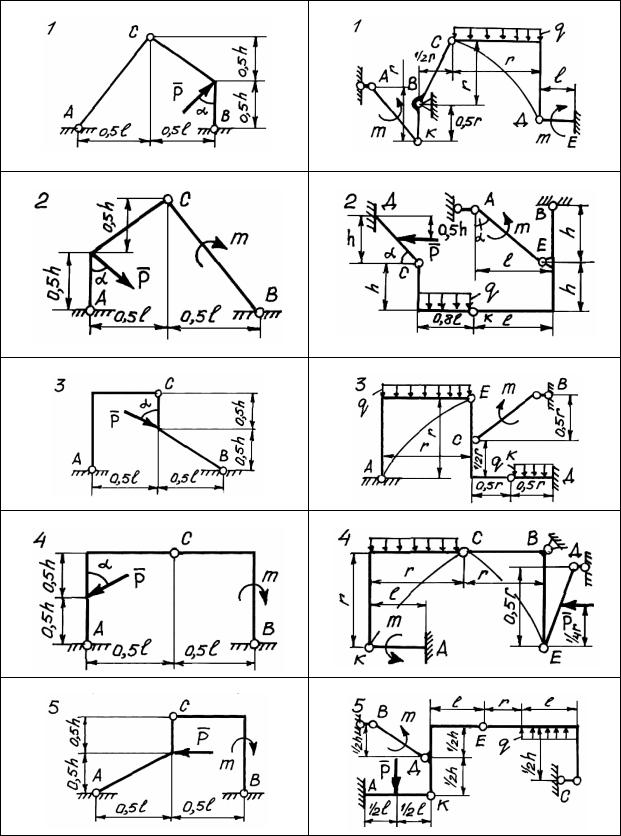
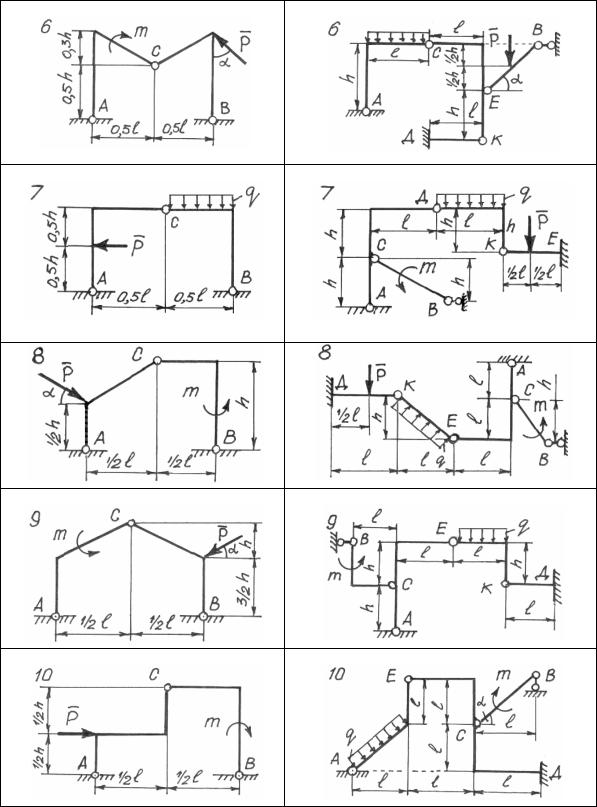
Для составных конструкций рам, изображенных на рис. 43 – 48, требуется определить реакции опор.
Заданы следующие величины для всех вариантов двух задач: P = 10 кН – сосредоточенная сила; m = 5 кНм – момент пары сил; q = 4 кН/м – равномерно распределенная нагрузка; a = 2 м; l = 6 м; h = 4 м; r = 3 м – геометрические размеры конструкций; α = 30о.
Для заданных сочлененных конструкций в статике существует два способа расчета. При решении данных двух задач следует использовать любой из известных способов.
Пример решения задач
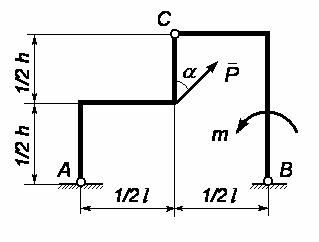
Задача № 1 Схема конструкции приведена на рис. 42.
Рис. 42
Дано: P = 10 кН; m = 5 кНм; l = 6 м; h = 4 м; α = 300.
Определить реакции в опорах A и B рамы.
64
Рис. 43
65
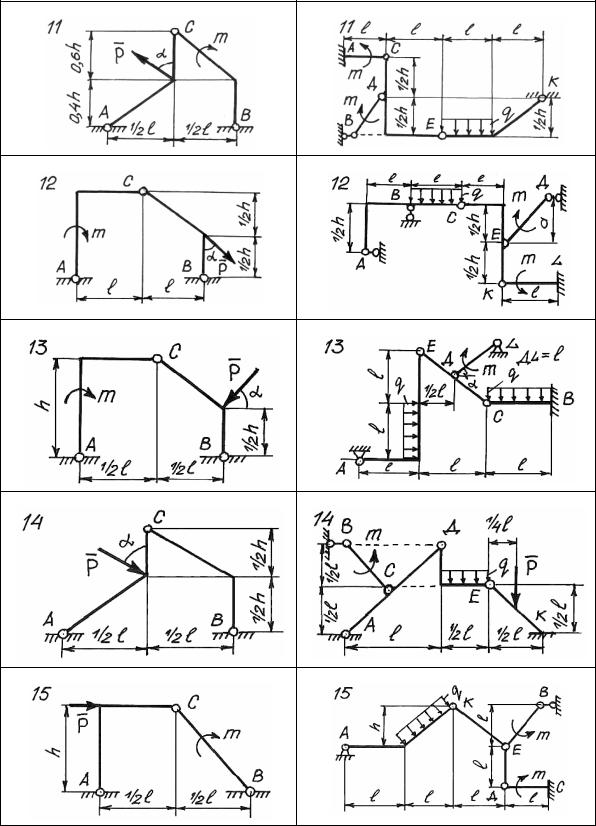
Рис. 44
66
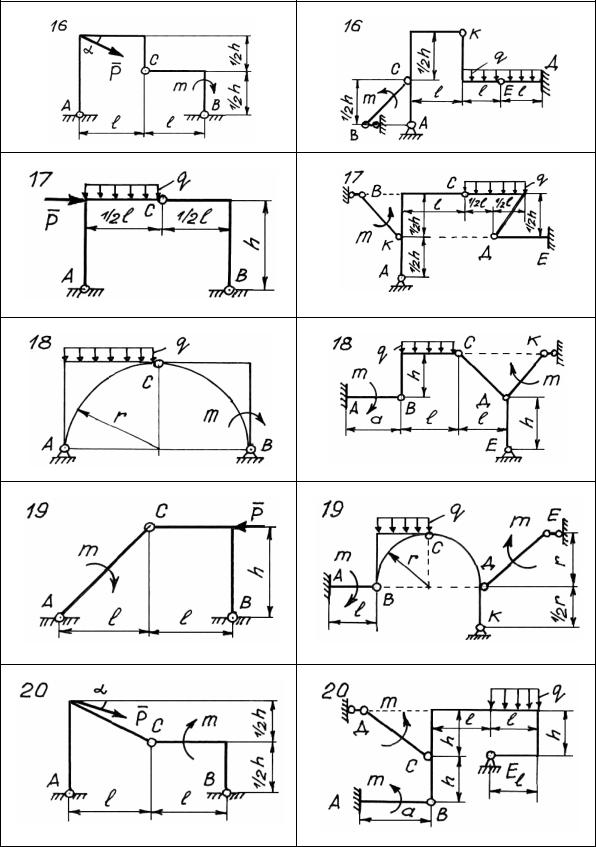
Рис. 45
67
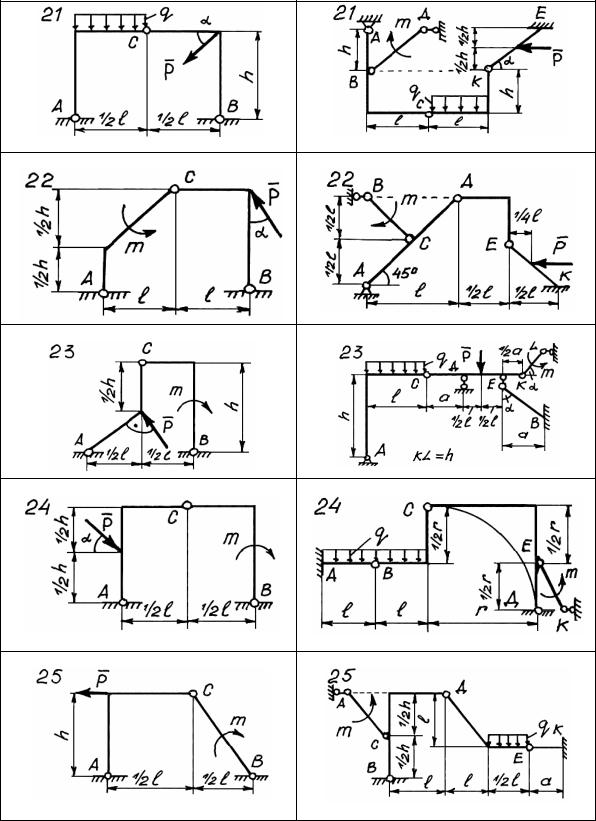
Рис. 46
68
Рис. 47
69
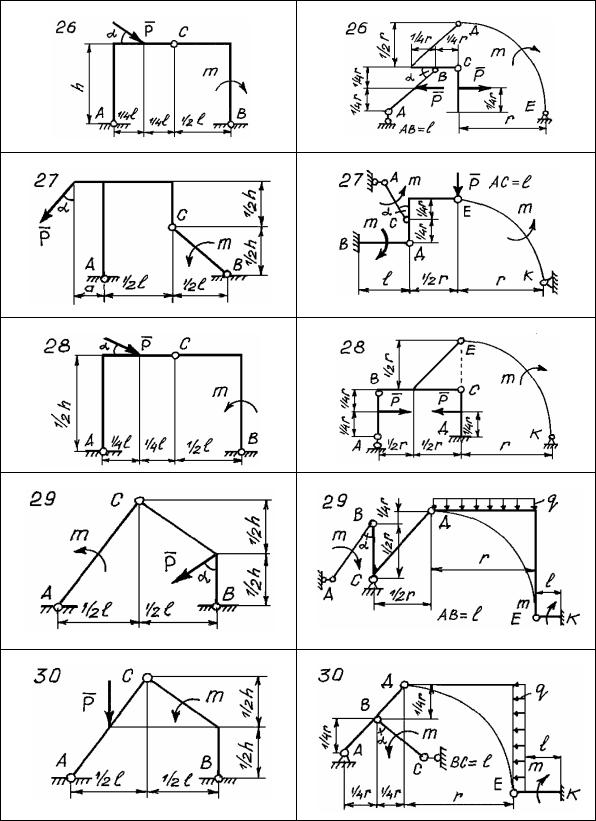
Рис. 48
