Теоретическая механика. Теория, задания и примеры решения задач (Б.Е.Ермаков)

Добавил:

DIF Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский автомобильно-дорожный государственный технический университет

Предмет:

Теоретическая механика

Файл:

(T −W )= 0

.pdf

Скачиваний:

4938

Добавлен:

04.06.2014

Размер:

9.68 Mб

Скачать

☆

<<< < Предыдущая 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 3334 / 3534 35 > Следующая >>>

330

Запишем систему уравнений для второго участка:

						v2	= P cos(ϕ +ϕ1) + N;
				m		R	= P cos(ϕ +ϕ1) + N;
						R		(7)
								(7)
				m dv = P sin(ϕ +ϕ ) − Nf.
						dt	1
						dt
В системе (7), исключая N, запишем
		dv	+ f	v 2	= g sin(ϕ +ϕ ) + gf cos(ϕ +ϕ );
		dt		R			1	1
		dt		R
а при z =	v2	будем иметь
а при z =	R	будем иметь
	R
z′ + 2fz = 2g sin(ϕ +ϕ1) + 2gf cos(ϕ +ϕ1)								или

z′ + 2fz = g(2cosϕ1 − 2f sinϕ1)sinϕ + g(2sinϕ1 + 2f cosϕ1)cosϕ.

В окончательном виде
z′ + 0,2z =11,6 sinϕ +15,9cosϕ.				(8)
Решение (8) будет: z = z + z ,		где z =C e−0,2ϕ ,
1	2	1	1
а z2 =C2 sinϕ +C3 cosϕ ;	z2′	=C2 cosϕ −C3 sinϕ .
Тогда

C2 cosϕ −C3 sinϕ + 0,2C2 sinϕ + 0,2C3 cosϕ =11,6sinϕ +15,9cosϕ .

Составляем систему уравнений для определения C2 и C3:

C2 + 0,2C3 =15,9 ,

0,2C2 −C3 =11,6 .

Решая полученную систему уравнений, находим:

	C =17,5м/ с2 ;	C = −8,1м/ с2 .
	2	3
Тогда	z = C e−0,2ϕ +17,5 sinϕ −8,1cosϕ.
	1
Для начальных условий ϕ0 = 0;		z(ϕ0 ) = v12	= 6,76 м/ с2	;
		R

		331
находим C =14,9 м/ с2 .
1
Квадрат скорости на втором участке как функция параметра ϕ
		v2 =14,9e−0,2ϕ +17,5 sinϕ −8,1cosϕ.	(9)
Из (7) находим реакцию нормального давления:
N = m	v2	− mg cos(ϕ +ϕ ), а с учетом (9) получим:
N = m		− mg cos(ϕ +ϕ ), а с учетом (9) получим:
	R	1
	R

N =14,9e−0,2ϕ + 24,8 sinϕ −14,6cosϕ.

Определим угол ϕ2, при котором реакция нормального давления во второй раз будет равна нулю.

Составим программу для N(ϕ2) = 0.

	ϕ2 := 3
	given
14,9e−0,2ϕ2	+ 24,8sinϕ2 −14,6cosϕ2 = 0
	z := minerr(ϕ2 )
z = 3,913;	ϕ2 = 3,913	рад = 224,2D.

Определим скорость в этой точке по формуле (9).

v22 =14,9e−0,2 3,913 +17,5sin224,2D −8,1cos224,2D = 0,41м2 / с2.

Тогда, v2 = 0,64 м/ с при N(ϕ2) = 0.

Третий участок

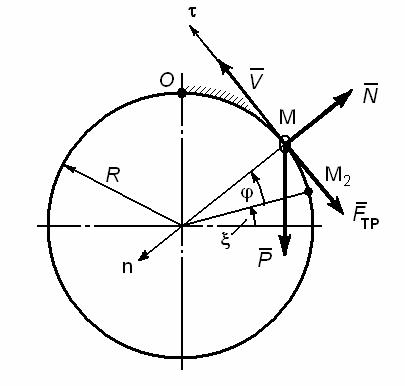
При угле больше 224,2О реакция N меняет направление, и поэтому следует рассмотреть третий участок (рис. 196).

Третий участок начинается от точки M2, где

ξ = ϕ1 + ϕ2 − 270D = 48,2D + 224,2D − 270D = 2,4D.

Запишем два уравнения в естественных осях координат:

	v2	= P cos(ϕ +ξ) − N,
m	R

	dv
		= P sin(ϕ +ξ) −Nf.
m	dt

332

		Рис 196
В полученной системе, исключая N, запишем
	z′ − 0,2z = 9,8 sinψ −1,96cosψ,		(10)
где	z = z(ϕ); ψ = ϕ +ξ;	dψ = dϕ.
Решение (10) будет в виде: z = z1 + z2,
где	z1 = C1e0,2ϕ; z2 = C2 sinψ +C3 cosψ; z2′ = C2 cosψ −C3 sinψ.

После подстановки z2 и z2′ в (10) получим:

C2 cosψ −C3 sinψ −0,2C2 sinψ − 0,2C3 cosψ = 9,8 sinψ −1,96cosψ.

Из полученного тождества составляем систему двух уравнений:

C2 − 0,2C3 = −1,96,

0,2C2 +C3 = −9,8.

Решая систему, находим: C = −3,77 м/ с2;	C = −9,05 м/ с2.
2	3

Тогда, z = C1e0,2ϕ − 3,77 sin(ϕ +ξ) − 9,05cos(ϕ +ξ).

				333
Используя		начальные		условия на третьем		участке - ϕo = 0;
z(ϕo ) =	v22	= 0,41м/ с	2	; ξ = 0,0419рад = 2,4	D
z(ϕo ) =	R	= 0,41м/ с		; ξ = 0,0419рад = 2,4		, находим:
	R

C1 = 0,41+ 3,77 sin2,4D + 9,05cos2,4D = 9,61м/ с2.

Окончательно запишем квадрат скорости точки на этом участке: v2 = 9,61e0,2ϕ − 3,77 sin(ϕ + 2,4D) −9,05cos(ϕ + 2,4D). (11)

Когда v(ϕ3 ) = 0 , то будет мгновенная остановка колечка на окружности. При этом нужно выражение (11) приравнять нулю и отно-

сительно ϕ3 решить трансцендентное уравнение. Программа для решения трансцендентного уравнения

будет иметь вид:

ϕ3 := 2 given

9,61e0,2ϕ3 − 3,77sin(ϕ3 + 0,0419) −9,05cos(ϕ3 + 0,0419) = 0 z := minerr(ϕ3 )

z = 0,149; ϕ3 = 0,149 рад = 8,54D.

Следовательно, колечко пройдет по окружности, не меняя направления скорости до мгновенной остановки при угле

α = ϕ1 +ϕ2 +ϕ3 = 48,2D + 224,2D + 8,54D = 280,94D 4,9 рад.

Длина дуги окружности при этом составит S = αR = 4,9 м.

В дальнейшем, после мгновенной остановки, колечко начнет обратное движение, так как

tg(360D − 280,94D) = tg(79,06D) = 5,17 >f = 0,1.

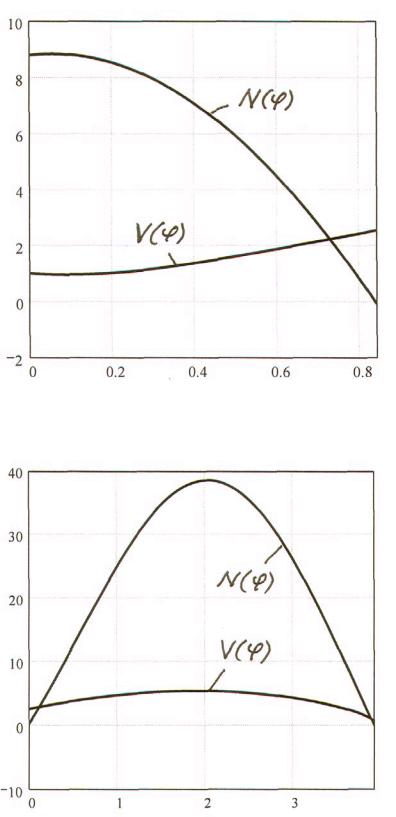
Изменение скорости и реакции нормального давления в зависимости от угла ϕ для первого и второго участков показаны на рис. 197.

334

Первый участок

Второй участок

Рис. 197

335

Приложение 2. Элементы новизны в аналитической механике

Все существующие выводы дифференциальных уравнений движения (как голономных, так и неголономных) механических систем базируются на принципе Даламбера с использованием возмущения (δt = 0)движения точек системы при помощи их возможных пере-

мещений δrk или возможных скоростей δvk , или возможных ускоре-

ний δak .

Уравнение Лагранжа второго рода

Одним из основных уравнений в аналитической механике является уравнение Лагранжа.

Рассмотрим уравнение Лагранжа второго рода для голономных механических систем:

d	∂T	−	∂T	= Q	(i =		),
						1, s		(1)

dt ∂qi				i
			∂qi

где T =T (qi ,qi ,t) - кинетическая энергия механической системы;

Q	=	(δAk )i	- обобщенная сила;

i		δqi

s – число степеней свободы механической системы.

Пусть задана голономная механическая система с идеальными и склерономными связями так, что кинетическая энергия этой системы будет являться функцией только обобщенных скоростей –

T =T (q

,...,q

∂T

d ∂T

∂T

Тогда для уравнения (1)

= 0,

∂

dt qi

336

∂rk

но для механической системы

Обобщенная сила Qi = ∑Fk

∂q

k =1

со склерономными связями можно записать тождество Лагранжа

∂

∂v

∑Fk

∂vk

. Тогда Qi =

∂qi

Пусть в системе действуют силы Fk

= Fk (c,

,t), тогда

∂

(∑Fkv

k )= ∂∂W ,

∂

где W = ∑Fkvk - мощность активных сил.

С учетом полученных выводов уравнение (1) приобретает новый вид

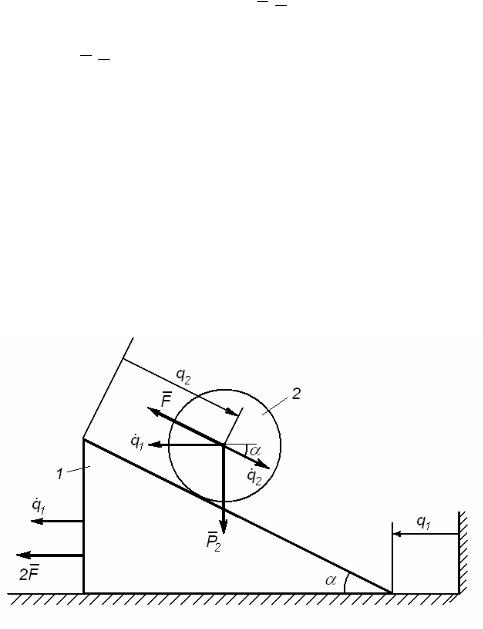
Пример На рис. 198 показана голономная механическая система с двумя

степенями свободы: q1 = q1(t); q2 = q2(t).

Рис. 198

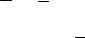
337

Цилиндр 2 массой m2 катится по наклонной грани призмы 1, массой m1, под действием сил F и P2 . Призма перемещается по гладкой поверхности под действием силы 2F .

Зная угол α, определить ускорение призмы и относительное ускорение центра масс цилиндра.

Решение

Запишем уравнение (2) для обобщенной скорости q1 и q2 :

									∂		(T −W )= 0;												∂						(T −W )= 0.																		(3)
									∂		(T −W )= 0;												∂						(T −W )= 0.																		(3)
										q														q		2
										1																2
	Вычислим кинетическую энергию:
							T =T					+T				=	1 m v				2	+			1 I ω2								+	1 m v2						,
											1		2				2		2		2				2				2		2			2				1 1
где		v	2	=	2		+	2		−						cos		α	;	ω =								q2		; I				=		1		m r		2		; v	2	=		2	.
где		v		=	2		+	2		−						cos		α	;	ω =										; I				=				m r				; v		=		2	.
			2		1				2			1 2										2						r					2		2				2 2				1			1
							= 1											+ 3											2
	Тогда				T		= 1			(m		+					2	+ 3							2				−									cos		α		и
	Тогда				T			2		(m			m )q						4		m q									m q q								cos				и
								2			1				2		1		4			2					2					2		1			2
	=	dT		=	1	(m		+								+	3								−										cos				α −							cos		α	.
T	=			=				+								+									−														α −									α
T		dt			2					m )q q							2	m q				q							m q q												m q q
		dt			2		1				2	1		2			2		2		2			2						2		1		2								2	1		2

Определяем мощность всех сил действующих в системе:

W= 2Fq1 −Fq2 + Fq1 cosα + P2q2 sinα = (2 + cosα)Fq1 − Fq2 + m2gq2 sinα.

Окончательно получим:

(T −W ) = (m1 + m2 )q1a1 + 32 m2q2a2 − m2q2a1 cosα −

−m2q1a2 cosα −(2 + cosα)Fq1 + Fq2 − m2gq2 sinα .

Используя (3), запишем систему двух алгебраических уравнений для определения а1 и а2:

338

Неизвестные величины определяем по способу Крамера.

∆ =

(m1 + m2 )

−m2 cosα

+ m (1+ 2sin2

α)

−m2 cosα

2 m2

∆1 =

F(2 + cosα)

−m2 cosα

m2 [F(6 + cosα) + m2g sin2α],

(m g sinα

− F )

∆2 =

(m1 + m2 )

F(2 + cosα)

−m cosα

(m g sinα −F )

= m (m + m )g sinα + F(2m cosα − m sin2 α − m ).

Тогда

a =

∆1 ,

∆2 .

∆

a1 =

F(6 + cosα) + m2g sin2α

3m + m (1+ 2sin2

α)

2(m + m )g sinα + 2F(2cosα − sin2 α − m1 )

a =

3m + m (1+ 2sin2

α)

Чтобы а2 не поменяло знак, нужно положить, что m2gsinα > F.

2.2. Принцип возможных скоростей

Если механическая система со склерономными (стационарными), идеальными и двусторонними связями находится в покое, то уравнение (2) приобретает следующий вид:

	339
∂W
∂W	= 0 (i =1,s).	(5)
∂	= 0 (i =1,s).	(5)
qi

С помощью уравнения (3) можно определить зависимость между силами, действующими на механизм, а также находить реакции связей в статически определимой конструкции.

Пример

Под действием сил P , Q и пары сил с моментом M плоский механизм находится в равновесии (рис. 199).

При известных величинах M, α, β, l1 определить силы P и Q.

			Рис. 199
Решение
Плоский механизм имеет две степени свободы:
ϕ1 =ϕ1(t); xA = xA(t) - независимые координаты.
При этом v1	=		=ϕ	= ω
При этом v1		xA и v2	1l1	1l1.
Для нашего случая запишем два уравнения на основе (3):
			∂W = 0;		∂W = 0.	(6)
			∂v1		∂v2

Определяем мощность заданных сил.

W =Qv1 + Mω1 − Pvc cosγ .

<<< < Предыдущая 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 3334 / 3534 35 > Следующая >>>

Соседние файлы в предмете Теоретическая механика

#
04.06.20149.68 Mб4938Теоретическая механика. Теория, задания и примеры решения задач (Б.Е.Ермаков).pdf
#
04.06.201439.42 Кб69Экзаменационные билеты. 2004-2005. КМ.doc
#
04.06.201427.14 Кб42Экзаменационные билеты. 2006г. 4семестр. КМ,ГП.doc