Теоретическая механика. Теория, задания и примеры решения задач (Б.Е.Ермаков)

290

Задача Д.10. Колебания механической системы с одной степенью свободы около устойчивого положения равновесия

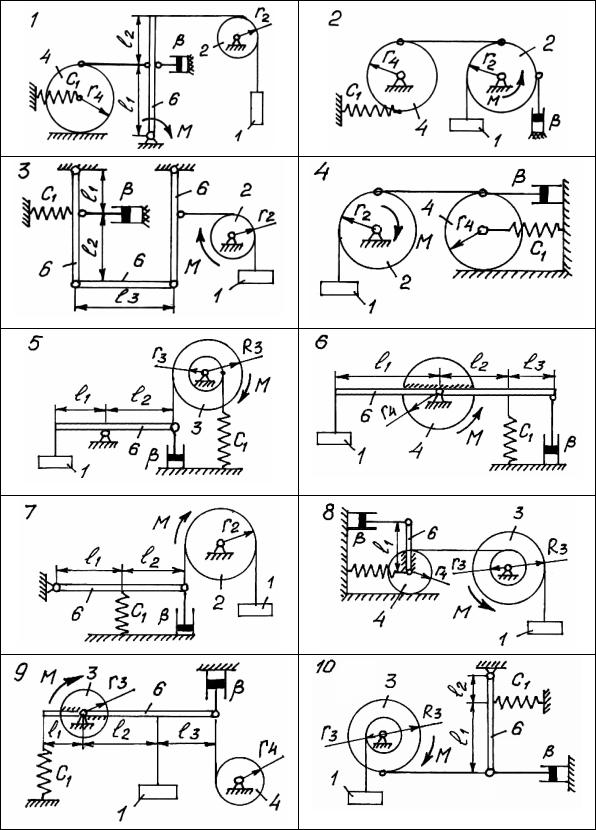
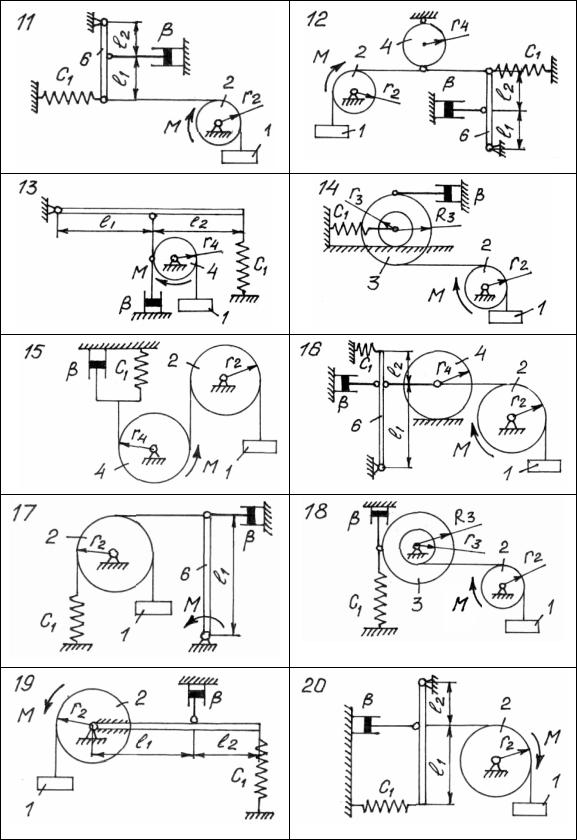
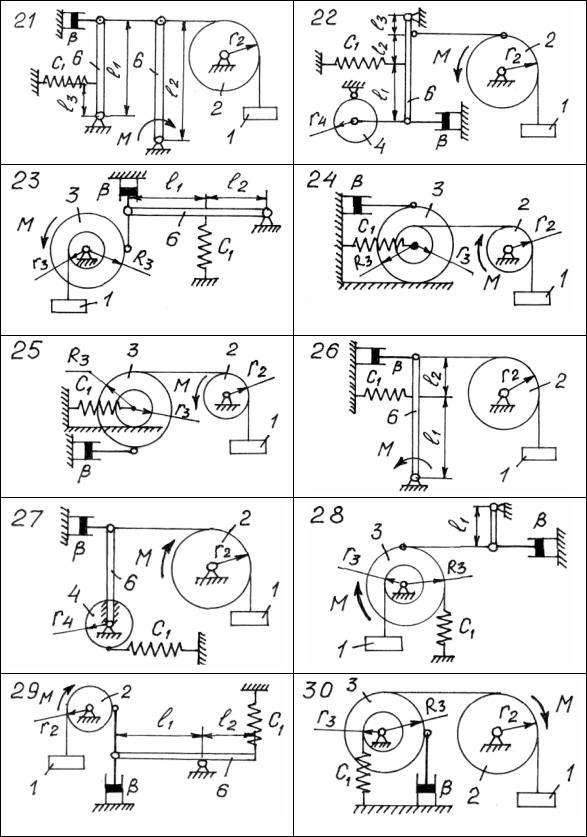
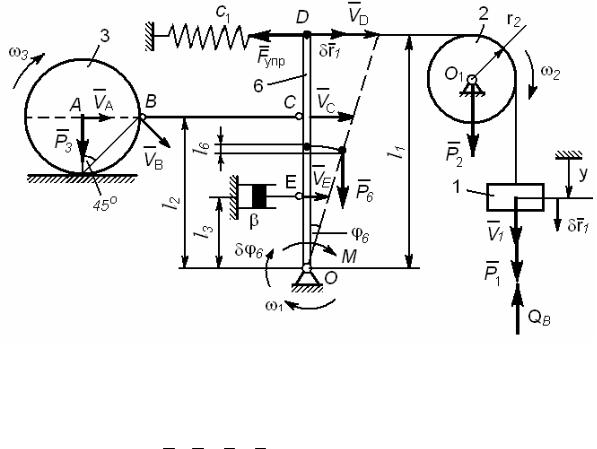
Механическая система с одной степенью свободы, с идеальными и удерживающими связями, показана на рис. 183 – 185 в положении равновесия. Числовые значения параметров механической системы, начальных условий и возмущающего момента приведены в таблице 17, где Λ - логарифмический декремент затухания.

Возмущающий момент изменяется по закону M = Mo sin pt , где МО - амплитуда и p - частота возмущающего момента. При расчетах принимать R3 =1,5r3 , а обобщенной координатой считать координату y=y(t) тела 1, которая отсчитывается от равновесного положения.

Определить:

1. Уравнение свободных колебаний (отключен демпфер β и возмущающий момент М) и статическую деформацию пружины.

2. Уравнение свободных колебаний при действии сил сопротивления (отключен возмущающий момент М) и коэффициент сопротивления β демпфера.

3. Уравнение вынужденных колебаний при действии сил сопротивления.

Рассчитать и построить графики амплитудно-частотной характеристики (АЧХ) и фазо - частотной характеристики (ФЧХ).

1.Свободные колебания механической системы без учета сил сопротивления.

Колебательным движением механической системы называют ее малые отклонения как в одну, так и в противоположную сторону в окрестности устойчивого положения равновесия.

291

Рис. 183

292

Рис. 184

293

Рис. 185

294

Таблица 17

295

Если в системе действуют только консервативные силы и нет сопротивления, то это свободные колебания.

Для механической системы с одной степенью свободы запишем уравнение Лагранжа 2-го рода. При Q = − ∂∂Пq и ∂∂Tq = 0

где a - обобщенный коэффициент инерции;

c - обобщенный коэффициент жесткости упругих элементов системы;

q, q - обобщенная координата и обобщенная скорость точки.

колебаний механической системы.

Линейному дифференциальному уравнению (3) соответствует общее решение

q =C1 cos kt +C2 sinkt и q = −C1k sinkt +C2k cos kt .

лебаний.

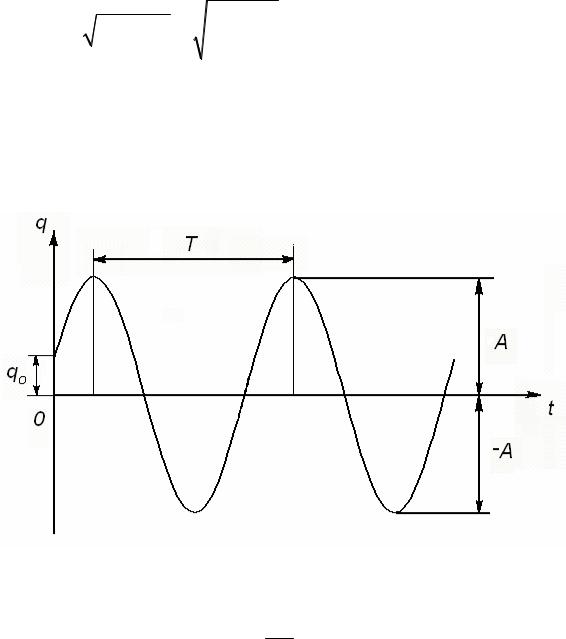
Развертка свободных колебаний показана на рис. 186.

Рис. 186

На графике обозначены: T = 2kπ (с) - период колебаний;

297

A - амплитуда колебаний; 2A - размах колебаний; q0 = Asinγ - начальное отклонение.

Пример решения задачи Д. 10.1

Для механической системы (рис. 1876) заданы следующие величины: m1 = 2кг, m2 = 2кг, m3 = 3кг, m6 = 6кг массы тел; l1= 0,6м; l2 = 0,4м; l3 = 0,2м; r2 = 0,2м; r3 = 0,4м; c1 = 400н/м – коэф-

фициент жесткости пружины; y0 = 0,02м; y0 = 0,2м/с – начальные условия.

Требуется определить уравнение свободных колебаний y=y(t) заданной механической системы.

Рис. 187

Решение

На схеме рис. 187 покажем скорости характерных точек тел механической системы: v1, vD,vC ,vA .

Запишем связи между этими скоростями.

298

При q = y уравнение Лагранжа второго рода для консерватив-

ных сил будет иметь следующий вид:

d ∂T + ∂П = 0. dt ∂y ∂y

Вычисляем кинетическую энергию системы.

T =T1 +T2 +T6 +T3 ;

T3 = 21 m3vA2 + 21 I3ω32 .

Так как диск 3 сплошной и однородный, то

Окончательно

где а- обобщенный коэффициент инерции.

299

Запишем геометрические связи между характерными точками системы:

Вычисляем потенциальную энергию механической системы.

П = П(Р1) + П(с1) + П(Р6 ), а для сил тяжести P2, P3 точки приложения А и O1 не меняют своей высоты.

П(Р1) = −А(Р1) = −Р1 y = −m1g y ;

П(c1) = −A(c1) = 21 c1λ2 .

Деформация пружины λ = λст + SD = λст + y , поэтому

П(с1) = 21 с1(λст + у)2 ;

c1λcт − m1g = 0.