Добавил:

DIF Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский автомобильно-дорожный государственный технический университет

Предмет:

Теоретическая механика

Файл:

Теоретическая механика. Теория, задания и примеры решения задач (Б.Е.Ермаков)

.pdf

Скачиваний:

4938

Добавлен:

04.06.2014

Размер:

9.68 Mб

Скачать

☆

<<< < Предыдущая 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 2728 / 3528 29 30 31 32 33 34 35 > Следующая >>>

270

где a = m

ρ2

r 2

+ m

- коэффициент инерции (приве-

2 R22

3 R22

денная масса).

T =

1 ax2 , T =T (x).

Распишем левую часть уравнение Лагранжа:

∂T

= ax ;

∂T

= 0 ;

∂T = ax .

∂x

dt ∂x

Определяем обобщенную силу по формуле:

Q = (δδAxk ) .

Тогда δA = F δr1 cosγ − Fтр1δr1 − P3 δr3 При P3 = m3g , Fтр1 = fm1g + fF sinγ , Mc3

δr = δx, δr =		r2	δx, δϕ	3	=

1	3	2R2

sinα − Mc3δϕ3 .

= km3g cos α,

r2		δ x ,
2r R		δ x ,
2r R
3	2

будем иметь

δA =

F(cosγ −f sinγ ) −fm g − m g

(sinα +

cosα)

δ x .

Окончательно

Q = F(cosγ −f sinγ ) −fm g − m g

(sinα +

cosα).

Тогда получим ax = Q , откуда x = Q ,

F(cosγ −f sinγ ) − fm g − m g(sinα +

cosα)

a1 =

ρ2

r 2

+ m

R22

271

Задача Д.8. Дифференциальные уравнения движения механической системы

в обобщенных координатах (Уравнение Лагранжа второго рода)

Механическая система (рис. 175 – 177) состоит из твердых тел и нерастяжимых нитей. При движении тел трение скольжения отсутствует. Заданная механическая система – голономная с двумя степенями свободы, имеет стационарные (склерономные) и двусторонние связи. В вариантах встречаются следующие обобщенные

координаты: s = s(t); x = x(t); ϕ = ϕ(t); ϕ1 = ϕ1(t); ϕ2 = ϕ2(t); x1 = x1(t); x2 = x2(t).

Используя уравнения Лагранжа второго рода, определить ускорение тех тел, обобщенные координаты которых заданы. В вариантах 9, 20, 22, 30 механизмы расположены в горизонтальной плоскости. Все данные для расчета приведены в таблице 16.

Пример решения задачи

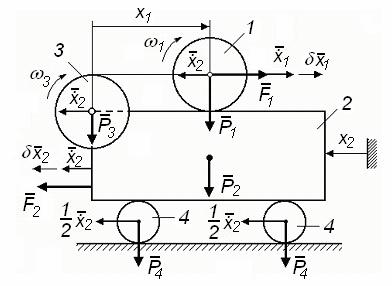
Голономная механическая система (рис. 178) состоит из твердых тел (1 – 4) и нерастяжимой нити между телами 1 и 3. Система движется под действием сил F1 и F2 . Обобщенные координаты x1, x2 показаны на чертеже. Заданы следующие величины: m1 = 4 кг;

m2 = 8 кг; m3 = 2 кг; m4 = 6 кг – массы тел; F1 = 10 Н; F2 = 40 Н –

действующие силы. Диск 1 и цилиндры 4 катятся без скольжения. Определить ускорение центра масс тела 1 и тела 2.

Решение

На рис. 178 показываем скорости всех тел, входящих в систему, выражая их через обобщенные скорости x1 и x2 .

272

Рис. 175

273

Рис. 176

274

Рис. 177

275

											Таблица 16

вариантаНомер	m1	m2	m3	m4	F	M	M1	M2	R1	R2	R3	R4
(рис.175-
(рис.175-	кг	кг	кг	кг	Н	Нм	Нм	Нм	м	м	м	м
177)	кг	кг	кг	кг	Н	Нм	Нм	Нм	м	м	м	м
1	4	8	2	3	-	-	-	-	-	-	-	-
2	10	6	10	-	6	2	-	-	0,8	-	0,8	-
3	8	4	6	-	4	-	-	-	-	-	-	-
4	10	6	12	-	7	-	-	-	-	-	-	-
5	6	4	10	-	-	-	-	-	-	-	0,6	-
6	6	10	4	-	6	-	-	-	-	-	-	-
7	10	12	6	8	2	-	-	-	-	-	-	-
8	6	8	4	4	-	-	-	-	-	-	-	-
9	8	9	6	-	-	-	2	3	1,2	-	0.4	-
10	10	8	4	6	-	-	-	-	-	-	-	-
11	4	6	2	-	-	-	-	-	-	-	-	-
12	6	8	2	-	4	-	-	-	-	-	-	-
13	2	4	2	-	-	-	-	-	-	-	-	-
14	4	6	8	10	-	2	-	-	-	-	-	0,5
15	4	2	6	-	5	4	-	-	-	-	0,6	-
16	2	4	6	5	-	-	-	-	-	-	-	-
17	4	8	6	-	6	-	-	-	-	-	-	-
18	3	6	8	10	-	-	-	-	-	-	-	-
19	2	4	6	10	-	-	-	-	-	-	-	0,8
20	6	8	4	2	-	-	8	4	-	0,8	0,6	0,5
21	2	4	2	6	-	-	-	-	-	-	-	0,4
22	4	8	3	6	-	-	2	6	-	0,8	0,4	0,6
23	5	6	8	2	-	-	-	-	-	-	-	-
24	3	8	4	-	-	-	-	-	-	-	-	-
25	6	8	4	-	6	-	-	-	-	-	-	-
26	2	4	6	8	-	8	-	-	-	-	-	-
27	4	8	2	-	4	-	-	-	-	-	-	-
28	4	2	6	8	-	12	-	-	-	-	-	0,8
29	8	10	4	2	5	-	-	-	-	-	-	-
30	4	6	6	-	-	-	8	2	-	0,6	0,6	-

276

Рис. 178

Вычисляем кинетическую энергию системы.

													n
									T = ∑Tk =T1 +T2 +T3 + 2T4 .
											k =1
	Тело 1 совершает плоское движение, поэтому
											T			=		1 m v					2 +		1 I ω					2 .
													1			2		1			1		2			1	1								x
														=			−																ω =		x
														=			−																ω =	1
Абсолютная скорость v												1			x			x		2	, угловая скорость												1				,
Абсолютная скорость v															x			x			, угловая скорость																,
																1																			R1
																																			R1
I	= 1 m R 2					-	момент инерции тела 1.
1	2	1		1
							=	1						−			2	+			1	1									2
							=	1						−			2	+			1	1							2 x1 =
Тогда					T				m (x						x		)							m R
Тогда					T				m (x						x		)							m R
						1		2		1 1						2					2 2					1 1 R12
	=	3			2		−						+		1					2 =		3					2			−			+ 1			2		;
		4	m x					m x x							2	m x						4			4x						4x x		2	4x				;
		4		1		1			1	1	2		=		2		1		2			4		+			1				1	2	2			2
										T			=				2 −							+						2	.
										T					3x					4x x			2			2x			2		.
											1					1					1		2						2

Тело 2 совершает поступательное движение, поэтому

T2 = 21 m2x22 = 21 8x2 = 4x22

277

T2 = 4x22 .

Тело 3 совершает плоское движение, поэтому

											T		=	1 m x							2		+ 1 I ω			2 .
				x							3			2				3			2		2	3	31
				x		и I					1					2
При ω			=		1				=		2	m R						,		находим
При ω			=	R					=			m R						,		находим
	3			R			3						3		3
	= 1				3	+ 1								= 1									2 + 1
	= 1				2	+ 1		1				2		= 1									2 + 1			2	=		2	+		2
T		m x								m x										2x					2x			x			0,5x		;
T	2	m x				2		2		m x						2				2x				4	2x			x			0,5x		;
3	2		3		2	2		2			3		1			2						2		4		1			2		1
													T		=					2 +				2	.
													T				x		2				0,5x		.
													3						2					1

Тело 4 совершает плоское движение, поэтому для однородных цилиндров кинетическая энергия

T4 = 34 m4v42 .

При v		=	1		, получаем	T =		3	m	2	=		3	2	.

	4		2	4		4	16		4	2		16		2

T4 =1,125x22 .

Окончательно запишем значение кинетической энергии системы в следующем виде:

T = 3,5x12 - 4x1x2 + 9,25x22 .

Для обобщенных координат x1 и x2 запишем уравнения Лагранжа второго рода:

	d ∂T		−	∂T		= Q ;

	dt ∂x			∂x
					1
1				1
d		∂T	−	∂T		= Q .

dt ∂x2				∂x2	2

Кинетическая энергия T =T (x1,x2 ) - функция только обобщенных скоростей, поэтому

278

∂T = ∂T = 0. ∂x1 ∂x2

Частные производные по обобщенным скоростям x1 и x2 :

∂T

−

;

∂T

−

∂x

18,5x

Полученные выражения дифференцируем по времени:

d	∂T		d	∂
		= 7x1 − 4x2 ;		T		= -4x1 +18,5x2 .
	∂		dt	∂
dt				x
	x1				2

На схеме рис. 177 показываем возможные перемещения центров масс тел 1 и 2.

Вычисляем обобщенные силы.

Обобщенная сила Q1 = (δAk )1 , при этом δ x1 ≠ 0, δ x2 = 0.

δ x1

(δAk )1 = F1δx1, тогда Q1 = F1 =10 кН.

Обобщенная сила Q =		(δAk )2	, при этом δ x2 ≠ 0, δ x1 = 0.
Обобщенная сила Q =			, при этом δ x2 ≠ 0, δ x1 = 0.
	2	δx2
		δx2
(δAk )2 = F2δx2 - F1δx2 =(F2 - F1 )δx2 . Тогда Q2 = F2 = 30 кН.

При x	= a (относительное ускорение тела 1) и			x	= a , окон-
1	1			2	2

чательно запишем систему двух алгебраических уравнений:

7a1 - 4a2 = 10;-4a1 +18,5a2 = 30.

Определитель коэффициентов при неизвестных a1 и a2

∆=	7	-4	=129,5 -16 =113,5.
∆=	7	-4	=129,5 -16 =113,5.
	-4	18,5

279


			∆ =		10		-4		= 185 +120 = 305;
			∆ =		10		-4		= 185 +120 = 305;
			1		30		18,5
					30		18,5
				∆2 =		7	10	= 210		+ 40 = 250 .
						7	10
						−4	30
Тогда a = ∆1		=		305		2,7м/с2 ;				a	= ∆2 =		250	2,2	м/с2 .
Тогда a = ∆1		=	113,5			2,7м/с2 ;				a	= ∆2 =	113,5		2,2	м/с2 .
1	∆		113,5							2	∆	113,5
Окончательный ответ:							a1 = 2,7 м/с2;				a2 = 2,2 м/с2.

<<< < Предыдущая 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 2728 / 3528 29 30 31 32 33 34 35 > Следующая >>>

Соседние файлы в предмете Теоретическая механика

#
04.06.20149.68 Mб4938Теоретическая механика. Теория, задания и примеры решения задач (Б.Е.Ермаков).pdf
#
04.06.201439.42 Кб69Экзаменационные билеты. 2004-2005. КМ.doc
#
04.06.201427.14 Кб42Экзаменационные билеты. 2006г. 4семестр. КМ,ГП.doc