
Теоретическая механика. Теория, задания и примеры решения задач (Б.Е.Ермаков)
.pdf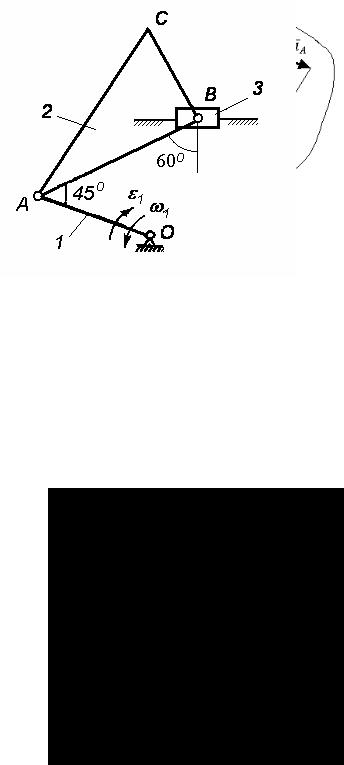
130
Рис. 90
Пример решения задачи К 3.1
На рис. 91 показана схема плоского механизма.
Исходные данные задачи: ω1 = 1,8 c-1; ε1 = 1,4 c-2; l1 = 1,5 м;
AB = 3 м; BC = 2 м.
Для заданного положения механизма требуется определить скорости и ускорения точек A, B, и C, а также угловую скорость и угловое ускорение звена 2.
Рис. 91
Решение
1)Описание видов движения каждого звена, входящего в плоский механизм.
131
Звено 1 (кривошип), ведущее звено, совершает вращение вокруг неподвижной точки О.
Звено 2 совершает плоское движение, при этом точка A этого звена перемещается по окружности, радиус которой равен l1, а точка B – по горизонтальной прямой.
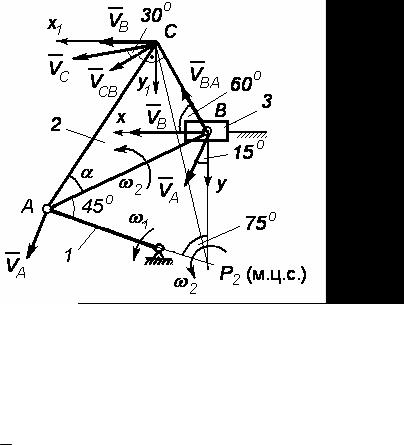
2)Определение скоростей точек механизма способом векторного сложения.
Расчет плоского механизма всегда начинаем от ведущего звена 1
(рис. 92).
Рис. 92
Скорость точки A, принадлежащей кривошипу 1, определяем по формуле
vA = ω1 l1 =1,8 1,5 = 2,7 м/с.
Вектор VA будет перпендикулярен звену 1 и направлен в сторону,
как показывает ω1.
Для вычисления скорости точки В, направление которой мы знаем, запишем векторное равенство, приняв за полюс точку A.
|
|
|
|
|
|
|
|
|
|
v |
B = v |
A +vB / A . |
(vB/A AB). |
||||||
|
– + + + – + |
|
|
|
|||||

132
В точке B показываем три вектора vB , vA и vB/A .
Через точку B проводим оси координат xBy и на эти оси проецируем векторное равенство.
x: vB = vAsin15o + vB/Acos60o ; y: 0 =VAcos15o -VB/Asin60o.
Из второго уравнения находим
vB/A = vA |
cos15o |
|
= 2,7 |
|
0,966 |
3,01м/с. |
|
sin60o |
|
0,866 |
|||||
|
|
|
|
|
|||
При этом vB/A = ω2 AB, откуда |
|
|
|
||||
ω = vB/A = 3,01 |
1с-1 |
. |
ω =1с-1. |
||||
2 |
AB |
3 |
|
|
|
|
2 |
|
|
|
|
|
|
||
Из первого уравнения находим VB .
vB = 2,7 sin15o + 3,01 cos60o 2,2м/с vB = 2,2м/с.
На схеме показываем ω2 около полюса – точки A и направляем в сторону, как указывает vB/A .
Для вычисления скорости точки C за полюс можно принять точку B и записать векторное уравнение
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
v |
C = v |
B +vC / B |
(vC/B BC ). |
|||||||||||||||
|
– – |
+ + |
|
|
+ + |
|
|
|
||||||||||||
|
|
|
C/B . |
|
|
|
|
|
|
|
|
|
||||||||
Вычислим модуль скорости v |
|
|
|
|
|
|
|
|
|
|||||||||||
|
vC/B = ω2 BC =1 2 = 2м/с. |
|||||||||||||||||||
|
|
|
|
C/B . |
|
|
|
|
||||||||||||
В точке C покажем векторы v |
B и v |
|
|
|
|
|||||||||||||||
Через точку C проводим оси |
|
x1C y1 |
и на эти оси проецируем вектор- |
|||||||||||||||||
ное равенство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x : |
|
v |
Cx |
1 |
= v |
B |
+ v |
C/B |
cos30o ; |
|||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
y1 : vCy1 = vC/Bsin30o.

133
Находим проекции скорости точки C.
vCx |
= 2,2 + 2 cos30o = 3,93 м/с; |
|
1 |
|
|
vCy |
= 2 sin30o =1м/с. |
|
1 |
|
|
Тогда скорость |
|
|
vC = vCx2 |
+ vCy2 = 1+ 3,932 4,06м/с. |
|
|
1 |
1 |
vC = 4,06м/с.
3)Определение скоростей точек при помощи мгновенного центра скоростей (МЦС).
При известной скорости VA = 2,7 м/с находим МЦС для звена 2. Для этого восстанавливаем перпендикуляры к вектору vA и на-
правлению скорости точки B, тогда их пересечение (т. P2) дает МЦС
звена 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Запишем пропорцию |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
vA |
= |
|
|
vB |
|
, |
|
|
откуда |
|
|
vB = BP2 vA . |
|
|||||||||
|
AP2 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
BP2 |
|
|
|
|
|
|
|
|
|
|
AP2 |
|
||||||||
Для определения BP2 и |
|
AP2 в треугольнике ABP2 |
применяем |
||||||||||||||||||||
теорему синусов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
AB |
|
= |
|
BP2 |
|
= |
|
AP2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin75o |
sin45o |
|
sin60o |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда |
BP = AB |
sin45o |
= 3 |
sin45o |
2,2м; |
|
|
|
|
||||||||||||||
|
|
|
|
|
2 |
|
|
|
sin75o |
|
|
|
sin75o |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
BP |
= |
sin45o |
= 0,816; |
|
|
|
|
AP = AB |
sin60o |
= 2,69м; |
|||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
AP2 |
|
sin60o |
|
|
|
|
|
|
|
|
|
2 |
|
sin75o |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
vB = 0,816 2,7 = 2,2м/с; |
|
|
vB = 2,2м/с. |
|
||||||||||||||||||
|
|
|
|
|
= 2,2 =1с-1 ; |
|
|
|
|
|
|
||||||||||||
При этом |
ω |
|
= |
vB |
|
|
|
ω =1с-1. |
|
||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
2 |
|
BP2 |
2,2 |
|
|
|
|
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
МЦС (точку P2) соединяем с точкой C и перпендикулярно CP2 показываем вектор скорости vC в сторону ω2 .
|
|
|
134 |
|
|
|
|
|
Тогда vC = ω2 CP2 . |
|
|
|
|
|
|
||
Введем угол α = CAB. |
tgα = BC |
= 2 |
; |
|
α = 33,7o. |
|||
|
|
|
AB |
3 |
|
|
|
|
Тогда |
CAB = 45o + 33,7o = 78,7o. |
|
|
|
|
|
||
Определим |
AC = AB2 + BC2 = 32 + 22 |
3,6м. |
||||||
По теореме косинусов вычисляем CP2 . |
|
|
|
|
|
|||
CP = |
AC2 + AP2 - 2AC AP cos78,7o |
= |
|
|
|
|
||
2 |
|
2 |
2 |
|
|
|
|
|
|
= |
3,62 + 2,692 - 2 3,6 2,69 cos78,7o 4,05м. |
||||||
Тогда |
vC = ω2 CP2 =1 4,05 = 4,05м/с; |
|
vC = 4,05м/с. |
|||||
|
|
|
|
|
|
|
|
|
Погрешность по сравнению с первым способом расчета составляет
∆% = 4,06 - 4,05 100 % 0,25%. 4,06
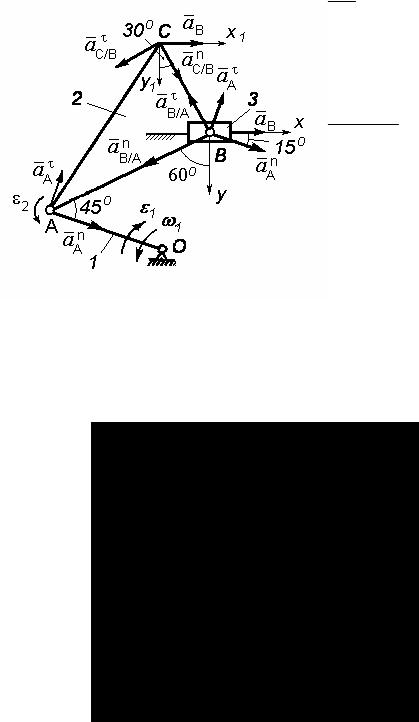
4)Определение ускорений точек A, B, C и углового ускорения звена 2.
При определении ускорений расчет также начинаем от ведущего
звена 1 (рис. 93).
Рис. 93
135
Ускорение точки A, которая перемещается по окружности, будет
|
|
|
aA = aAn + aAτ , |
|
(aAn aAτ ). |
|
an |
=ω2l =1,82 |
1,5 = 4,86м/с2 |
, |
aτ |
= ε l =1,4 1,5 = 2,1м/с2 . |
|
A |
|
1 1 |
|
|
A |
1 1 |
Тогда |
aA = (aAn )2 +( aAτ )2 = |
4,862 + 2,12 5,3м/с2 . |
||||
Вектор aAn направляем вдоль кривошипа 1 к оси вращения (т. О),
а вектор aτA – перпендикулярно кривошипу в сторону ε1 .
Вычисляем угол наклона вектора aA к кривошипу 1.
tgµ = |
|
aτA |
|
|
= |
2,1 |
= 0,4321, |
µ 23,4o. |
|
|
|||||||
|
|
|
|
|||||
|
aAn |
4,86 |
||||||
|
|
|
|
|
||||
Запишем векторное равенство для вычисления ускорения точки B.
a = a n |
+ aτ |
+ an |
+ aτ |
, |
(aτ AB). |
||
B |
A |
A |
|
B/A |
B/A |
|
B/A |
|
|
|
|
|
|
||
– + + + |
+ + |
+ + |
– + |
|
|
||
Определим модуль ускорения aB/An .
aB/An =ω22 AB =1 3 = 3м/с2 .
Все пять векторов показываем в точке B. Проецируем векторное равенство на оси xBy.
x:aB = aAncos15o + aτAsin15o − aB/An cos30o − aB/Aτ sin30o ;
y:0 = aAnsin15o − aτAcos15o + aB/An sin30o − aB/Aτ cos30o.
Из второго уравнения полученной системы определим aBτ / A .
aτ |
= |
|
|
1 |
|
(4,86 sin15o + 3 sin30o − 2,1 cos15o ) ≈ 0,84м/ с2 |
|||||
|
|
|
|
|
|||||||
B / A |
|
|
cos30o |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
Но aτ |
A |
= ε |
2 |
AB , откуда ε |
2 |
= |
aBτ / A |
= 0,84 = 0,28с−2 . |
|||
|
|||||||||||
|
B / |
|
|
|
|
AB |
3 |
||||
|
|
|
|
|
|
|
|
|
|
||

136
ε2 = 0,28с−2 .
На схеме рис. 93 ε2 показываем относительно полюса A в сторону направления вектора aBτ / A .
Ускорение точки B
aB = 4,86 cos15o + 2,1 sin15o − 3 cos30o −0,84 sin30o = 2,2м/ с2 aB = 2,2м/ с2 .
Для вычисления ускорения точки C , за полюс принимаем точку B и записываем векторное равенство
a |
= a |
B |
+a n |
+ aτ , |
(aτ BC). |
C |
|
C/B |
C/B |
C/B |
|
|
|
|
|||
– – |
+ + |
+ + |
+ + |
|
|
Определим модуль векторов aC/Bn и aC/Bτ
aC/Bn =ω22 BC =1 2 = 2 м/с2 , aC/Bτ = ε2 BC = 0,28 2 = 0,56 м/с2 .
В точке C показываем три вектора - aB , aC/Bn , aC/Bτ . Вектор aC/Bn
правляем к полюсу (точке B), а вектор aC/Bτ - перпендикулярно
сторону ε2 .
Векторное равенство проецируем на оси координат x1Cy1.
на-
BC в
|
|
|
x1: |
a |
= a |
+ an |
sin30o |
− aτ |
|
cos30o ; |
||||
|
|
|
|
|
Cx |
B |
|
C/B |
|
|
C/B |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
y1: |
a |
= an |
|
cos30o + aτ |
|
sin30o . |
|||||
|
|
|
|
|
Cy |
C/B |
|
C/B |
|
|
|
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
Тогда |
|
a |
= 2,2 + 2 sin30o −0,56 cos30o = 2,7м/ с2 ; |
|||||||||||
|
|
Cx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
= 2 cos30o +0,56 sin30o |
= 2м/ с2 . |
||||||||||
|
|
Cy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Модуль ускорения точки C |
|
|
|
|
|
|
|
|
||||||
a = |
a2 |
+ a2 |
|
= |
2,72 |
+ 22 = 3,36м/ с2 |
. |
|
a = 3,36м/ с2 . |
|||||
C |
Cx |
Cy |
1 |
|
|
|
|
|
|
|
C |
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
137 |
|
|
|
|
|
|
Направление вектора aC . |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
aCx |
2,7 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
; i ) = 36,5o . |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
cos(a; i ) = |
= 0,8036 ; |
(a |
|||||||||||||||
|
1 |
= |
|
|
|
|||||||||||||
|
|
|
|
|
||||||||||||||
|
|
1 |
|
aC |
3,36 |
|
|
|
|
C |
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Все полученные результаты сводим в таблицу 8. |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 8 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
vA |
|
vB |
|
vC |
|
w2 |
|
aA |
aB |
|
|
aC |
e2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
м/с |
м/с |
|
м/с |
|
с-1 |
|
м/с2 |
м/с2 |
|
м/с2 |
с-2 |
||||||
|
2,7 |
2,2 |
|
14,06 |
|
1 |
|
|
5,3 |
2,2 |
3,36 |
0,28 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример решения задачи К 3.2
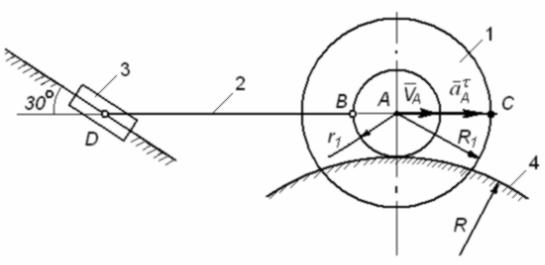
В плоском механизме (рис. 94) двухступенчатое колесо 1 может катиться без скольжения по неподвижной цилиндрической поверхности 4.
Заданы следующие величины: vA = 2 м/с; aτA = 1,8 м/с2; R1 = 3r1; r1 = 0,4 м; R = 2 м; l2 = 3 м.
Рис. 94
Для заданного положения механизма требуется определить скорости и ускорения точек A, B, C, D, а также угловые скорости и угловые ускорения звеньев 1 и 2.
138
Решение
1) Описание видов движения каждого звена, входящего в плоский механизм.
Звено 1 (двухступенчатое колесо), ведущее звено (vA , aAτ - известные величины), совершает плоское движение по неподвижной цилиндрической поверхности.
Звено 2 находится в плоском движении, при этом точка D этого звена перемещается по прямолинейной траектории.
Звено 3 перемещается поступательно по прямой, имеющей уклон
в30О к горизонту.
2)Определение скоростей всех точек механизма способом мгно-
венного центра скоростей (МЦС).
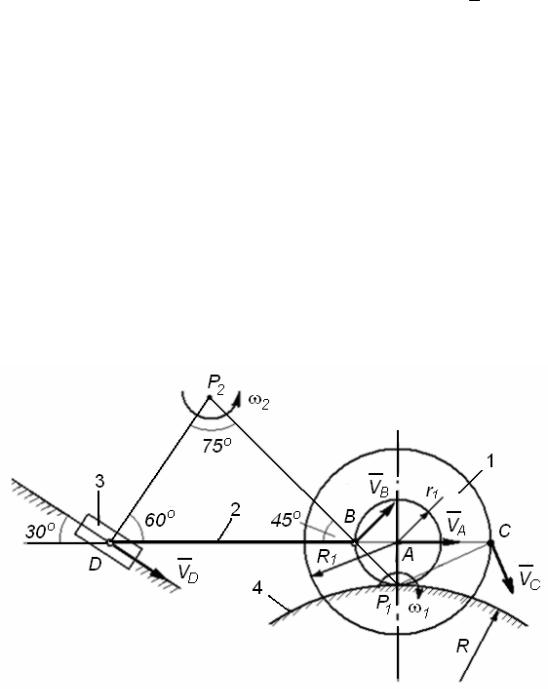
Так как звено 1 может катиться без скольжения по неподвижной цилиндрической поверхности 4, то точка контакта P1 у них общая, скорость этой точки равна нулю. Значит точка P1 – есть МЦС звена
1 (рис. 95).
|
|
|
Рис. 95 |
|
|
|
|
|
|
Тогда скорость v |
A |
= ω r , откуда ω = |
vA |
= |
2 |
= 5с−1. ω = 5с−1. |
|||
|
|
||||||||
|
1 1 |
1 |
r1 |
|
0,4 |
1 |
|
||
|
|
|
|
|
|
|
|
||

139
Точку P1 соединяем с точкой B и перпендикулярно BP1, в сторону
ω1, показываем |
|
|
B . |
По модулю vB = ω1 BP1, при этом |
вектор v |
||||
BP1 = r1 2 = 0,4 |
2 0,57м. |
VB = 5 0,57 2,83м/ с. |
||
|
|
vB = 2,83м/ с. |
||
Точку C соединяем с P1 и перпендикулярно CP1, в сторону ω1,
показываем вектор скорости vC . Модуль этой скорости
v |
C |
= ω CP . |
CP = |
r 2 |
+ R2 |
= r |
10 = 0,4 10 1,265м/ с. |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
Тогда |
vC = 5 1,265 6,32м/ с. |
vC = 6,32м/ с. |
||||
Для определения МЦС звена 2 нужно в точке B восстановить перпендикуляр BP2 к скорости vB , и в точке D восстановить перпендикуляр DP2 к наклонной траектории точки D, а пересечение этих перпендикуляров дает МЦС звена 2 (P2).
Запишем соотношение
vB |
= |
vD |
, |
vD = |
DP2 |
vB . |
|
|
|
||||
BP2 |
DP2 |
|
BP2 |
|||
При известных углах в треугольнике DP2B, вычислим стороны треугольника по теореме синусов.
|
AB |
|
|
= |
|
DP2 |
|
|
= |
|
BP2 |
|
, |
|
|
AB = l . |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
sin75o |
|
|
|
|
sin 45o |
|
|
|
sin60o |
|
|
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
DP |
|
sin 45o |
|
|
|
|
|
|
|
|
||||||||||
Откуда |
|
|
2 |
= |
sin60o |
= 0,8165 , |
|
|||||||||||||||
BP2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
BP = |
|
sin60o |
l |
|
= |
sin60o |
3 2,7м. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
sin75o |
2 |
|
|
|
sin75o |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Тогда vD = 0,8165 2,83 2,31м/ с. |
|
|
|
|
vD = 2,31м/ с. |
|||||||||||||||||
Угловая скорость звена 2 ω = |
vB |
= |
2,83 |
1,05с−1. |
||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
BP2 |
2,7 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ω2 =1,05с−1.
