Решение

Приведем данные к сравнимым единицам.

D = 20 единиц в неделю;

R = 125 ф. ст. на заказ;

И = 2 ф. ст. на единицу в неделю;

L = 2 недели. Подставив эти значения в уравнение, получим

Объем повторного заказа = время на выполнение заказа х спрос =

= LD - 2 ∙ 20 = 40 единиц.

Таким образом, лучшая политика — размещать заказ на 50 единиц всякий раз, когда запас опускается до 40 единиц.

Проблема здесь заключается в том, что объем запаса никогда не повысится до 60 единиц, а будет меняться до 0 до 50 единиц. Есть способ, позволяющий это учесть: вычисленный объем по­вторного заказа относится одновременно к имеющимся запасам и к размещенному заказу. Поэтому объем повторного заказа равен спросу за время выполнения заказа минус любые запасы, которые уже заказаны. В примере, приведенном выше, объем заказа состав­ляет 50 единиц, поэтому время выполнения 3 недели будет приво­дить к ситуации, когда один заказ еще не будет выполнен, а уже настанет время размещать другой. Тогда

объем повторного заказа = время выполнения заказа х спрос — объем уже размещенного заказа = LD — Q = 3 • 20 - 50 = 10 единиц.

Заказ на 50 единиц должен размешаться всякий раз, когда фак­тический запас снижается до 10 единиц. Поскольку время выпол­нения заказа дольше цикла запаса, всегда будет выполняться по крайней мере один заказ (рис. 10.6).

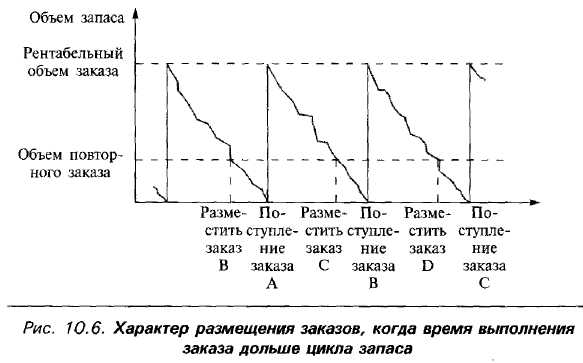
Конечно, возникает проблема: время на выполнение заказа может быть непостоянным. Мы знаем, насколько долгим это вре­мя было в прошлом, и мы знаем текущие целевые показатели, но всегда возможны некоторые отклонения, и поставщик не всегда может выйти на заданные целевые показатели. В связи с этим помимо прогнозирования спроса нам также необходимо прогно­зировать время выполнения заказа, и поэтому на самом деле объем повторного заказа зависит от этих двух прогнозов.

Анализ чувствительности

Одна из проблем, связанных с расчетом рентабельного объема заказа, — то, что он может давать странные значения. Это воз­можно, например, потому, что предлагаются нереальные закупки, например, 88,39 шины. Конечно, мы можем округлить это значе­ние до 88 шин, но, может быть, можно заказать 90 или даже 100 шин? Окажет ли такое округление значительное влияние на общие затраты? На практике кривая общих затрат в области точки рентабельного объема заказа становится относительно плоской.

Оказывается, заказываемое количество можно увеличить до 156% рентабельного объема заказа или снизить до 64% этого объема, и при этом переменные затраты увеличатся только на 10%. Анало­гично, объем заказа можно повысить до 186% или снизить до 54% рентабельного, и при этом переменные затраты увеличатся только на 20%. Это одна из причин, по которой анализ EOQ так широко используется, так как, хотя вычисления здесь строятся на ряде допущений или упрощений, в любом случае общие затраты повы­шаются относительно оптимума медленно. Другими словами, EOQ дает хорошие рекомендации по объему заказа с учетом широкого диапазона обстоятельств (рис. 10.7).

Задача

Чэн Тау Ханг (Cheng Tau Hang) заметил, что спрос на продукт, по­ставляемый его компанией, постоянен и составляет 500 единиц в месяц. Себестоимость единицы 100 долл., к тому же известно, что затраты, выз­ванные нехваткой продукта, очень высокие. Отдел закупок в среднем от­правляет 3000 заказов в год; общие операционные издержки составляют 180 000 долл. За любые запасы приходится платить 15% их стоимости, услуги склада стоят 7%, а другие накладные расходы составляют 8% в год. Заказ выполняется за неделю, и это время постоянно.

Какова должна быть политика заказов по этому виду продукции? Каким станет объем повторного заказа, если время выполнения заказа увеличится до 3 недель? При каком диапазоне объемов заказа перемен­ные затраты не превышают 10% оптимальных? Каковы будут перемен­ные затраты, если заказ увеличится за один раз до 200 единиц?