Цель работы.

Ознакомление с методами компьютерного моделирования электронных схем в MC-7 на основе построения электрических фильтров и изучения их характеристик.

Электрические фильтры

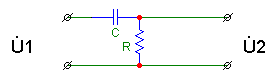Электрические схемы, исследуемые в данной работе, после упрощения сводятся к двум основным типам – к схеме, изображенной на рис.1, и к схеме на рис. 2.

Рис.1 Рис.2

Символ обозначает резистор.

Из теории электрических цепей известно, что цепь 1-го типа имеет следующие частотные характеристики:

А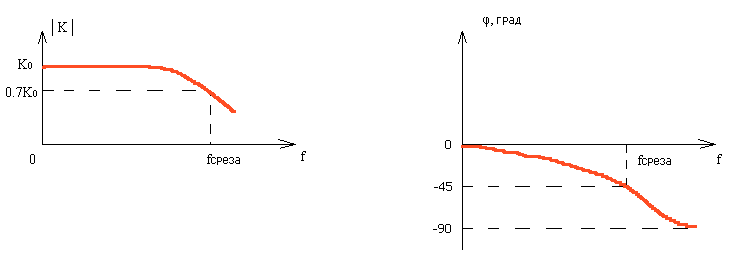 ЧХ : K(f) ФЧХ: φ (f)

Рис.3

Как видно из рис.3, │K(f)│ и φ(f) имеют следующие предельные значения:

│K(f → 0)│→ 1 │K(f→ ∞)│→ 0

φ(f → 0) → 0 φ(f → ∞) → -π/2

Из предельных выражений видно, что данная цепь пропускает низкие частоты и задерживает верхние, т.е. является фильтром нижних частот (ФНЧ).

Полоса пропускания фильтра определяется частотой среза f_среза.

f_среза – частота, на которой модуль коэффициента передачи ФНЧ уменьшается в заданное число раз. Обычно используют частоту среза по уровню 0.707. Тогда f_среза – частота, на которой модуль коэффициента передачи ФНЧ уменьшается в √ 2 раз. Для нашей цепи выражение для f_среза имеет следующий вид:

f_среза= 1 / 2RC = 1/2 , где =RC – постоянная времени цепи. На частоте f_среза φ = -45˚

Графики частотных характеристик для 2-го типа цепи (рис.2) приведены на рис.4.

АЧХ : K(f) ФЧХ: φ (f)

Рис.4

Предельные значения │K(f)│ и φ(f):

│K(f→0)│→ 0 │K(f→ ∞)│→ 1

φ(f →0) → -π/2 φ(f → ∞) → 0

Как видно, данная цепь пропускает высокие частоты и задерживает низкие, т.е. является фильтром верхних частот (ФВЧ). Частота среза по уровню 0.707 определяется тем же выражением, что и для ФНЧ, построенном по схеме рис.1:

f_среза= 1 / 2RC = 1/2 , где =RC – постоянная времени цепи.

Исследование частотных характеристик на ЭВМ нужно производить в диапазоне: 0 < f ≤ 5…10 f_среза

Переходная характеристика (реакция фильтра на импульсный сигнал)

Спектр прямоугольного сигнала содержит основную гармонику и высшие нечетные гармоники. Низкие частоты спектра формируют вершину прямоугольного сигнала, а вы-сокие частоты спектра – его фронт. Отсюда следует, что при прохождении прямоугольно-го сигнала через фильтр его форма будет искажаться, причем искажения будут зависеть от типа фильтра: ФНЧ будет искажать фронт импульса, а ФВЧ – вершину.

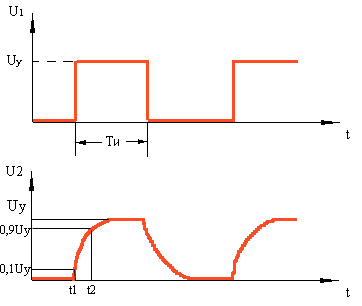
Рис.5

Форма напряжения на выходе схемы 1-го типа (ФНЧ) показана на рис.5. Напря-жение на выходе будет описываться следующими выражениями:

U₂(t) = U_y (1-e^-t/τ) на участке 0 < t < T_и

U2(t) = U_y e^-t/τ на участке t > T_и

При t = τ напряжение на участке 0 < t < T_и U₂(τ) = U_y (1-e)=0.632 U_y.

На участке t > T_и U₂ (τ) = U_y/e=0.368U_y, т.е. за время t = τ напряжение уменьшается в е раз..

Искажения фронта импульса оценивают по времени установление фронта. Время ус-тановления определяется отрезком времени, в течение которого напряжение нарастает от 0,1 до 0,9 от установившегося значения.

τ_y = t₂ – t₁ (см рис.5), или τ_y = 2.2 τ

На рис.6 показана форма напряжения на выходе цепи 2-го типа (ФВЧ):

Рис.6

Форма напряжения на участке плоской вершины определяется выражением

U2(t) = U_y e^-t/τ , 0 < t < T_и

Искажения вершины импульса характеризуется спадом вершины Δ. Спад вершины – это относительное изменение выходного напряжения за длительность импульса Т_{и .}

Δ% = [( U_y-U_k)/ U_y]100%;

Δ ≈ (Т_и/ τ)100%.