2. Расчет на прочность по методу Бринка.

К проектировочным расчетам относятся расчеты различных его элементов на прочность, стойкость при выстреле, а также расчет на устойчивость снаряда на траектории.

Проверим снаряд на прочность при выстреле. При его движении на этапе внутренней баллистики на снаряд действуют силы:

1. Давление пороховых газов.

2. Силы инерции, возникающие под действием поступательного и вращательного движений.

3. Радиальная сила реакции ВП вследствие его врезания в канал ствола.

4. Остаточные напряжения в материале корпуса снаряда.

Последние 3 силы и сила инерции вращения пренебрежимо малы по сравнению с остальными. Кроме того, не существует достоверных данных о распределении остаточных напряжений в общем случае, что вынуждает их также исключить из расчета.

Расчетное давление определяется по формуле:

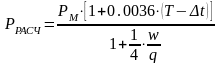(11)

где - максимальное давление в канале ствола орудия при выстреле, 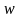- масса метательного заряда, 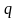- масса снаряда.

Осевая сила инерции рассчитывается по формуле:

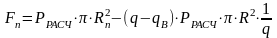(12)

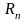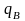где - текущий радиус рассматриваемого сечения, - наседающая масса снаряда (масса снаряда, находящаяся выше расчетного сечения), 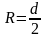- полукалибр снаряда.

Радиальная сила инерции рассчитывается по формуле:

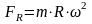(13)

где 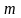- неуравновешенная масса, 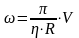- угловая скорость, 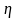- длина хода нарезов, 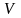- линейная скорость.

Окончательная формула для расчета осевой силы имеет вид:

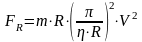(14)

Касательная сила инерции рассчитывается по формуле:

(15)

При расчете методом Бринка используется ряд гипотез:

1. Рассматривается полый цилиндр с эквивалентными размерами и нагруженный осевой силой инерции ( )

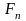2. Пластические деформации не допускаются, корпус снаряда находится в упругом состоянии.

3. Принцип независимости действия сил.

Расчет деформаций от осевой силы .

Деформации корпуса снаряда в осевом направлении рассчитывается по формуле:

(16)

где 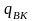- наседающая масса корпуса, 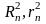- соответственно внешний и внутренний радиус рассматриваемого сечения, - модуль упругости Юнга для материала корпуса.

Деформации корпуса снаряда в радиальном направлении рассчитывается по формуле:

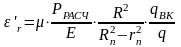(17)

где - коэффициент Пуассона для материала корпуса.

Деформации корпуса снаряда в касательном направлении рассчитывается по формуле:

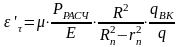(18)

Напряжения, возникающие в корпусе снаряда, вычисляются по формулам:

(19)

Критерием прочности корпуса снаряда является выполнение условия:

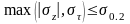(20)

Исходные данные

Таблица 22

Параметры	Проектируемый МЭС
Максимальное давление в канале ствола	343,4
Масса снаряда, кг	0,397
Наседающая масса снаряда, кг	0,211
Наседающая масса корпуса, кг	0,07
Внешний радиус сечения, мм	14,9
Внутренний радиус сечения, мм	10
Масса метательного заряда, кг	0,117
Длина хода нарезов, клб	23,8
Модуль Юнга для материала корпуса, МПа	2.1*105
Коэффициент Пуассона для материала корпуса	0,35
Условный предел текучести, МПа	510

Результаты расчета

Таблица 23

Параметры	Проектируемый МЭС
Расчетное давление, Мпа	357,8
Осевые деформации, м	-2,4*10-3
Радиальные деформации, м	0,8*10-3
Тангенциальные деформации, м	0,8*10-3
Осевые напряжения (максимальные), МПа	505