4.3 Визначення залежностей. Повний факторний експеримент. Властивості матриці плану. Отыскание зависимостей

В общем случае задача ставиться след. образом: с помощью ИИС в соотв. с выбранным планом реализуется эксперимент в результате которого получен массив данных. Располагая полем корреляции необходимо построить модель ( аналитическую зависимость) между входной и выходной величиной, которая бы с выбранным критерием оптимальности адекватно отображала бы поведение объекта.

План эксперимента показывает число и условие проведения опыта( эксперимент распадается на отдельные опыты).

Исходим из того ,что на объект может подаваться (может зависеть) несколько независимых величин. Х1, Х2,…, Хn . И объект имеет 1 выход. Вых. величина обознач. Y, - эксперимент. и наз. откликом.

Задачей исследов. явл. установление зависимостей.

, где Х1, …, Хn – факторы

Предполагая, что независимые величины , которые носят название факторы задаются или измеряются с меньшей погрешностью, чем отклик, причём погрешность измерения отклика подчиняется нормальному закону.

Таким образом имеем:

Х_i – задаем или измеряем

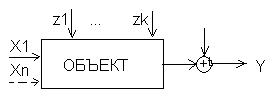
z1, zk – влияющие величины о которых мы ничего не знаем и которые измерить не можем.

- случайная погрешность измерений

- экспериментально полученные данные, искажённые погрешностью .

- оценка Y с учетом .

Задание: найти зависимость

Отклонение от Y , зависит от и влияния факторов z1, zk.

Любая модель приближение. Оценка является величиной случайной.

Ввиду того, что при проведении опытов влияние случайной величины, то после обработки результатов измерений приходим к оценке отклика .

Наличие случайности и ограниченный объём исследований само по себе приводит к тому, что полученная оценка будет отличаться от Y(мат.ожидания) и модель будет неадекватная, но помимо этого существует ряд факторов, влияющих на объекты, которые мы не можем учесть и это тоже явл. причиной неадекватности.

Таким образом из-за влияния учитываемых факторов, а также случайностей, имеет место поле корреляции.

Р

азобьём интервал корреляции, заключенный между Хmin i Xmax на элементарные участки . Для каждого элементарного участка вычисляем среднее значение и отложим в качестве координат по отношению к середине интервала и соединим их. Получим ломаную, которая наз. экспериментальной линией регрессии.

Если будем уменьшать длину элементарного интервала и одновременно увеличивать, но быстрее число опытов, то придём к теоретической линии регрессии, которая показывает какое в среднем примет значение выходная величина при многократном ее измерении. Факторы при этом являются фиксированными. Это условное математическое ожидание (Y при условии х).

Т.о. линия регрессии является геометрическим местом точек условных математических ожиданий.

Задачей исследования как раз и является построение зависимости, которая бы адекватно отображала поведение объекта .

В качестве критерия выбирается:

- метод наименьших квадратов,

где - значение, получено в результате проведения опытов в i-той точке факторного пространства(плоскости), если 1 фактор.

- это значение выходной величины , полученной на основе предполагаемой математической модели для тех же точек факторного пространства в которых проводиться исследование.

N – число точек, над которыми проводится исследование.

Если в каждой i-той точке проводиться по m измерений, то вместо будет - среднее: