
- •33.Магнитное поле в вакууме
- •34. Движение заряженных частиц в магнитном поле.
- •35. Взаимодействие магнитного поля с током.
- •36 Рамка с током в магнитном поле.
- •37 Поток вектора магнитной индукции сквозь произвольную поверхность.
- •38 Работа по перемещению проводника с током в магнитном поле.
- •39 Электромагнитная индукция.
- •40 Явление самоиндукции.
- •41Энергия магнитного поля тока.
- •42. Закон полного тока.
- •43 Магнитные свойства вещества.
- •44 Магнетики в магнитном поле.
- •45 Ферромагнетизм.
- •46. Основы единой теории электромагнитного поля Максвелла.
- •Электромагнитные колебания в колебательном контуре.
- •Электромагнитные волны.
Электромагнитные волны.
Возникновение электромагнитных волн. Волновое уравнение и его решение. Скорость волны. Свойства электромагнитных волн. Энергия электромагнитной волны, плотность энергии. Вектор Умова-Пойнтинга.
Электромагни́тное излуче́ние (электромагнитные волны) — распространяющееся в пространстве возмущение (изменение состояния)электромагнитного поля.
Возникновение электромагнитных волн связано с испусканием излучающим телом квантов энергии, или фотонов. Поток фотонов имеет наряду с корпускулярной природой свойства электромагнитных волн.
В многомерном случае однородное волновое уравнение записывается в виде
![]() ,
,
где ![]() — оператор
Лапласа,
— оператор
Лапласа, ![]() —
неизвестная функция,
—
неизвестная функция, ![]() —
время,
—
время, ![]() —
пространственная переменная,
— фазовая
скорость.
—
пространственная переменная,
— фазовая
скорость.
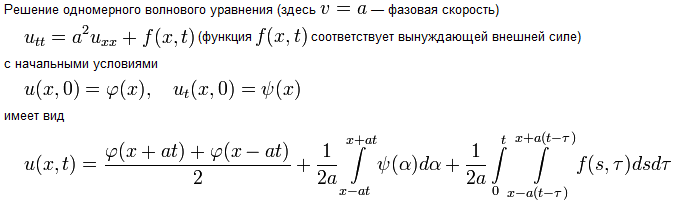
Скорость
волны:![]() Полученная формула показывает,
что скорость
волны равна произведению длины волны
на частоту колебаний в ней.
Полученная формула показывает,
что скорость
волны равна произведению длины волны
на частоту колебаний в ней.
Основными свойствами электромагнитных волн являются: поглощение; рассеяние; преломление; отражение; интерференция; дифракция; поляризация.
Объемная плотность энергии электромагнитного поля в линейной изотропной среде равна сумме объемных плотностей энергии электрического и магнитного полей полная плотность энергии электромагнитной волны равна
Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компоненттензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:
где E и H — векторы напряжённости электрического и магнитного полей соответственно
Явление интерференции. Когерентность световых волн. Определение результирующей интенсивности при интерференции двух когерентных световых волн. Оптическая разность хода. Условия интерференционных минимумов и максимумов. Интерференция двух плоских волн Откуда
с учетом:
Явление интерференции происходит при взаимодействии двух и более волн одинаковой частоты, распространяющихся в различных направлениях. При этом оно наблюдается и у волн, распространяющихся в средах, и у электромагнитных волн Две световые волны являются когерентными, если равны частоты и постоянен сдвиг фаз: ν1 = ν2, Δφ = const При интерференции световых волн удобнее иметь дело не с амплитудами, а с интенсивностями. Это не меняет существа дела, так как интенсивность пропорциональна квадрату амплитуды. Если в какую-либо точку приходят две волны с интенсивностями I1 и I2 и фазами φ1 и φ2 соответственно, то результирующая интенсивность в этой точке определяется выражением
где ∆φ = |φ1 – φ2| — разность фаз, а множитель γ отражает степень когерентности волн. Из этой формулы наглядно видна зависимость результирующей интенсивности от разности фаз ∆φ и от величины γ Оптическая разность хода. Условия интерференционных минимумов и максимумов. смотреть воп. 50
Ход лучей. Оптическая разность хода интерферирующих лучей. Изменение фазы волны на границе раздела двух сред. Условия интерференционных минимумов и максимумов. Просветление оптики. Кольца Ньютона: условия наблюдения, вид интерференционной картины. При освещении тонкой пленки происходит наложение волн от одного и того же источника, отразившихся от передней и задней поверхностей пленки. При этом может возникнуть интерференция света. Если свет белый, то интерференционные полосы окрашены. Интерференцию в пленках можно наблюдать на стенках мыльных пузырей, на тонких пленках масла или нефти, плавающих на поверхности воды, на пленках, возникающих на поверхности металлов или зеркала
Оптическая
разность хода-это разность оптических
длин путей световых волн, имеющих
общую начальную и конечную точки. Луч
света, проходя через плёнку толщиной множителем Изменение фазы волны на границе раздела двух сред При зеркальном отражении света, как явствует из формул Френеля, фаза отражённого света в общем случае скачкообразно изменяется. Если α = 0 (свет падает нормально к границе раздела), то при n2 > n1 фаза отражённой волны сдвигается на p, при n2 < n1 — остаётся неизменной.n-показатель преломления.
Просветле́ние о́птики — это нанесение на поверхность линз, граничащих с воздухом, тончайшей плёнки или нескольких плёнок одна поверх другой. Это необходимо для увеличения светопропускания оптической системы. Ко́льца Нью́тона — кольцеобразные интерференционные максимумы и минимумы, появляющиеся вокруг точки касания слегка изогнутой выпуклой линзы и плоскопараллельной пластины при прохождении света сквозь линзу и пластину Условия наблюдения интерференции Рассмотрим несколько характерных случаев: 1. Ортогональность поляризаций волн. При
этом 2.
В случае равенства частот волн 3.
В случае 4.
В случае Интерференционная картина в виде концентрических колец (колец Ньютона) возникает между поверхностями одна из которых плоская, а другая имеет большой радиус кривизны(например, стеклянная пластинка и плосковыпуклая линза). Исаак Ньютон исследовав их в монохроматическом и белом свете обнаружил, что радиус колец возрастает с увеличением длины волны (от фиолетового к красному).
Явление дифракции. Принцип Гюйгенса-Френеля. Метод зон Френеля. Расчет амплитуды результирующего колебания в некоторой точке при дифракции Френеля на круглом отверстии. Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий Явление дифракции заключается в том, что звуковые волны огибают преграды, линейные размеры которых меньше длины волны. Короткие волны отражаются от таких препятствий, образуя за ними звуковую тень. Принцип Гюйгенса — Френеля Каждый элемент волнового фронта можно рассматривать, как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн. Метод зон Френеля смотреть 52 вопрос Расчет
амплитуды результирующего колебания
в некоторой точке при дифракции
Френеля на круглом отверстии
Дифракция Фраунгофера на щели. Построение зон Френеля. Условия минимума и максимума дифракции на щели. Вид дифракционной картины в случае монохроматического и белого света. Дифракционная решетка. Условие главных максимумов. Тип дифракции, при котором дифракционная картина образуется параллельными пучками, называется дифракцией Фраунгофера. Параллельные лучи проявятся, если источник и экран находятся в бесконечности. Практически используется две линзы: в фокусе одной – источник света, а в фокусе другой – экран. Если на щель малой ширины падает параллельный пучок света, как показано на рис. 1, то вследствие явления дифракции свет попадает в том числе и в область геометрической тени. На экране наблюдается картина чередующихся полос максимумов и минимумов. Условие нахождения в определенной
точке экране минимума имеет вид:
где b – ширина щели, фи - угол, под которым видна интересующая нас точка экрана, лямда - длина волны падающего света, n – порядок минимума. Метод зон Френеля Френель предложил метод разбиения фронта волны на кольцевые зоны, который впоследствии получил название метод зон Френеля. Пусть от источника света S распространяется монохроматическая сферическая волна, P - точка наблюдения. Через точку O проходит сферическая волновая поверхность. Она симметрична относительно прямой SP. Разобьем эту поверхность на кольцевые зоны I, II, III и т.д. так, чтобы расстояния от краев зоны до точки P отличались на l/2 - половину длины световой волны. Это разбиение было предложено O. Френелем и зоны называют зонами Френеля. Возьмем произвольную точку 1 в первой зоне Френеля. В зоне II найдется, в силу правила построения зон, такая соответствующая ей точка, что разность хода лучей, идущих в точку P от точек 1 и 2 будет равна l/2. Вследствие этого колебания от точек 1 и 2 погасят друг друга в точке P.
Из геометрических соображениях следует, что при не очень больших номерах зон их площади примерно одинаковы. Значит каждой точке первой зоны найдется соответствующая ей точка во второй, колебания которых погасят друг друга. Амплитуда результирующего колебания, приходящего в точку P от зоны с номером m, уменьшается с ростом m, т.е.
Условие дифракционных максимумов от одной щели
Условие дифракционных минимумов от одной щели
При освещении щели белым светом центральный максимум наблюдается в виде белой полоски; он общий для всех длин волн (при = 0 разность хода равна нулю для всех ). Боковые максимумы радужно окрашены, так как условие максимума при любых m различно для разных . Таким образом, справа и слева от центрального максимума наблюдаются максимумы первого (m = 1), второго (m = 2) и других порядков, обращенные фиолетовым краем к центру дифракционной картины. Однако они настолько расплывчаты, что отчетливого разделения различных длин волн с помощью дифракции на одной щели получить невозможно. Дифракционная решётка — оптический прибор, действие которого основано на использовании явления дифракции света. Представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность Условия интерференционных максимумов дифракционной решётки, наблюдаемых под определёнными углами, имеют вид:
Свет естественный и поляризованный. Физическая сущность процесса поляризации Степень поляризации. Поляризатор и анализатор. Закон Малюса. Поляризация света - Возникает, когда свет под определенным углом падает на поверхность, отражается и становится поляризованным Естественный свет - это свет, в котором колебания вектора напряженности Е электрического поля происходят по всевозможным направлениям в плоскости, перпендикулярной направлению распространения (к лучу). Плоскополяризованный свет - это свет, в котором колебания вектора Е происходят только в одном направлении, перпендикулярном лучу. Частично поляризованный свет - это свет, в котором колебания в каком-либо направлении ослаблены. Физический смысл вектора электрической поляризации — это дипольный момент, отнесенный к единице объема диэлектрика. i-интенсивность
колебания Степень поляризации:
Поляриза́тор —- устройство, предназначенное для получения полностью или частично поляризованного оптического излучения из излучения с произвольным состоянием поляризации. В поляризационных микроскопах поляризаторы применяются в следующих частях: поляризатор (поляроид) нижней оптической системы, включённый постоянно. Анализатор (поляроид) верхней оптической системы, используемый, в частности, для наблюдения интервереционной окраски. Может быть и включён, и выключен.
Закон
Малюса —
физический закон, выражающий зависимость
интенсивности линейно-поляризованного света после
его прохождения через поляризатор от
угла
где
Поляризация света при отражении от поверхности диэлектрика. Плоскости поляризации отраженного и преломленного луча. Закон Брюстера. Стопа Столетова. Двойное лучепреломление, обыкновенный и необыкновенный луч. Если угол падения света на границу раздела двух диэлектриков (например, на поверхность стеклянной пластинки) не равен нулю, отраженный и преломленный лучи оказываются частично поляризованными (при отражении от проводящей поверхности (например, от поверхности металла) получается эллиптически поляризованный свет). В отраженном луче преобладают колебания, перпендикулярные к плоскости падения (на рис. 1 эти колебания обозначены точками), в преломленном луче - колебания, параллельные плоскости падения (на рисунке они изображены двусторонними стрелками). Степень поляризации зависит от угла падения. При угле падения, удовлетворяющем условию: (где n12 - показатель преломления второй среды относительно первой), отраженный луч полностью поляризован (он содержит только колебания, перпендикулярные к плоскости падения). Степень поляризациипреломленного луча при угле падения, равном iB, достигает наибольшего значения, однако этот луч остается поляризованным только частично. Зако́н Брю́стера — закон оптики, выражающий связь показателей преломления двух диэлектриков с таким углом падения света, при котором свет, отражённый от границы раздела диэлектриков, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения. При этом преломлённый луч частично поляризуется в плоскости падения, и его поляризация достигает наибольшего значения Закон Брюстера записывается в виде:
где Стопа Столетова Используется для получения полностью поляризованного света в отраженном пучке или частично поляризованного - после многократных прохождений Двойно́е лучепреломле́ние — эффект расщепления в анизотропных средах луча света на две составляющие. Если луч света падает перпендикулярно к поверхности кристалла, то на этой поверхности он расщепляется на два луча. Первый луч продолжает распространяться прямо, и называется обыкновенным (o — ordinary), второй же отклоняется в сторону, и называется необыкновенным (e — extraordinary).
Тепловое излучение нагретых тел и его особенности. Величины, характеризующие тепловое излучение (спектральная плотность энергетической светимости, интегральная энергетическая светимость), связь между ними. Спектральная поглощательная способность. Абсолютно черное тело. Закон Кирхгофа. В нагретых телах часть внутренней энергии вещества может превращаться в энергию излучения. Поэтому нагретые тела являются источниками электромагнитного излучения в широком диапазоне частот. Это излучение называют тепловым излучением. Способность теплового излучения находиться в равновесии с излучающим телом отличает тепловое излучение от других видов излучения тел. Поэтому, такое излучение, находящееся в равновесии с излучающим телом, будем называть равновесным. Спектральная плотность энергетической светимости — функция частоты и температуры, характеризующая распределение энергии излучения по всему спектру частот (или длин волн).
ПОГЛОЩАТЕЛЬНАЯ СПОСОБНОСТЬ тела - отношение поглощаемого телом потока излучения к падающему на него монохроматич. потоку излучения частоты v; Абсолютно чёрное тело — физическая идеализация, применяемая в термодинамике, тело, поглощающее всё падающее на него электромагнитное излучение во всех диапазонах и ничего не отражающее.
Закон
Кирхгофа. Отношение
излучательной способности любого
тела к его поглощательной способности
одинаково для всех тел при
данной температуре для
данной частоты и
не зависит от их формы и химической
природы.
Спектр излучения абсолютно черного тела. Закон Стефана – Больцмана. Закон смещения Вина. Квантовая гипотеза Планка Теплово́е излуче́ние или лучеиспускание — передача энергии от одних тел к другим в виде электромагнитных волн за счёт их тепловой энергии. Спектр излучения абсолютно чёрного тела определяется только его температурой.
где Смещение Винна λmax = b/T ≈ 0,002898 м·К × T −1 (K), где T — температура, а λmax — длина волны с максимальной интенсивностью. Коэффициент b, называемый постоянной Вина, в системе СИ имеет значение 0,002898 м·К.
Гипо́теза
Пла́нка — гипотеза,
выдвинутая 14
декабря 1900
года Максом
Планком и
заключающаяся в том, что при тепловом
излучении энергия испускается
и поглощается не непрерывно, а
отдельными квантами (порциями).
Каждая такая порция-квант имеет
энергию
где h или
Опыты Столетова. Вольтамперная характеристика (ток насыщения, задерживающее напряжение). Законы фотоэффекта. Уравнение Эйнштейна для фотоэффекта. Квантовая теория фотоэффекта. Внешним фотоэффектом (фотоэлектронной эмиссией) называется испускание электронов веществом под действием электромагнитных излучений В 1888 году Александр Григорьевич Столетов(1839–1896) исследовал фотоэффект более детально, фактически он независимо открыл это явление и обнаружил насыщение фототока. А. Г. Столетов использовал в своей установке металлический диск, который освещался через второй диск в виде сетки светом от электрической дуги. Металлическая пластина и сетка включались в цепь с гальваническим элементом и гальванометром. На сетку подавалось положительное напряжение, а на пластину – отрицательное. В этом случае в цепи возникал электрический ток.
Участок
насыщения.
При дальнейшем увеличении напряжения
на аноде рост тока замедляется, а затем
полностью прекращается, так как все
электроны, вылетающие из катода,
достигают анода. Дальнейшее увеличение
анодного тока при данной величине
накала невозможно, поскольку для этого
нужны дополнительные электроны, а их
взять негде, так как вся эмиссия катода
исчерпана. Установившейся в этом
режиме анодный ток называется током
насыщения.
Этот участок описывается законом
Ричардсона-Дешмана: Нелинейный участок. На начальном участке ВАХ ток медленно возрастает при увеличении напряжения на аноде, что объясняется противодействием полю анода объёмного отрицательного заряда электронного облака. По сравнению с током насыщения, анодный ток при Ua = 0 очень мал (и не показан на схеме). Его зависимость от напряжения растет экспоненциально, что обуславливается разбросом начальных скоростей электронов. Для полного прекращения анодного тока необходимо приложить некоторое анодное напряжение меньше нуля, называемое запирающим.
Рассеяние рентгеновского излучения на свободных электронах. Зависимость длины волны рассеянного излучения от угла рассеяния. Законы сохранения. Квантовая теория явления. Эффект Комптона (Комптон-эффект, Комптоновское рассеяние) — неупругое рассеяние фотонов на свободных электронах. Эффект сопровождается изменением частоты фотонов, часть энергии которых после рассеяния передается электронам. Происходит рассеяние фотонов на электронах — т. н. комптоновское рассеяние. В зависимости от угла рассеяния, длина волны фотона увеличивается на определённую величину и, соответственно, энергия уменьшается. Комптоновское рассеяние, по сравнению с фотопоглощением, становится преобладающим при более высоких энергиях фотона. Запишем уравнения, выражающие законы сохранения энергии и импульса: 1.энергия до столкновения (энергия фотона hν плюс энергия покоя электрона) должна равняться энергии после столкновения (энергия hν' рассеянного фотона плюс полная энергия получившего отдачу электрона) hν + moc2 = hν' + mc2, (1) где mo - масса покоящегося электрона, m - масса движущегося электрона, с - скорость света; 2.импульс падающего фотона p должен равняться сумме импульсов электрона pe и рассеянного фотона p' p = p' + pe (2)Энергия фотона связана с импульсом соотношением |p| = hν/c. (3) Может явления) Физические эффекты в квантовой теории поля, обусловленные внешними калибровочными полями, конечной температурой и плотностью вещества
Фотон. Масса и импульс фотона. Давление света (вывод). Корпускуля́рно-волново́й дуали́зм (или Ква́нтово-волново́й дуали́зм) — принцип, согласно которому любой объект может проявлять какволновые, так и корпускулярные свойства. Фото́н (от др.-греч. φῶς, род. пад. φωτός, «свет») — элементарная частица, квант электромагнитного излучения (в узком смысле —света). Это безмассовая частица, способная существовать только двигаясь со скоростью света.
Гипотеза де Бройля. Формула де Бройля. Опыт Девиссона – Джермера по дифракции электронов. Волновые свойства проявляются при распространении света (интерференция, дифракция).
Гипотеза
де Бройля устанавливает, что
движущейся частице, обладающей энергией
E и импульсом p, соответствует волновой
процесс, частота которого равна:
Формула де
Бройля устанавливает
зависимость длины волны
,
связанной с движущейся частицей
вещества, от импульса
где Опыт Дэвиссона-Джермера — физический эксперимент по дифракции электронов, проведённый в 1927 г. американскими учёными Клинтоном Дэвиссоном и Лестером Джермером. Наблюдалась дифракция электронов на кристаллической решётке монокристала. Опыт явился блестящим подтверждением существования у микрочастиц волновых свойств. 61.Соотношения неопределенностей. Неопределенность в определении координаты, импульса. Неопределенность в определении энергии частицы.
В.Гейзенберг
открыл так называемые соотношения
неопределенностей, в
соответствии с которыми
неопределенности координаты и импульса связаны
между собой соотношением:
Волновая функция, её статистический смысл. Свойства волновой функции, условие нормировки. Стационарное уравнение Шредингера для частицы в одномерной прямоугольной яме.
Волнова́я
фу́нкция,
или пси-функция Статический смысл: Интепретацию волновой функции дал в 1926 г. Борн: квадрат модуля волновой функции определяет вероятность того , что частица будет обнаружена в пределах объема dV: dP=|| 2 dV=*dV (17) где * - комплексно - сопряженная волновая функция. Величина || 2=* = dP/ dV - имеет смысл плотности вероятности.
Формулы (3.1) - (3.3) определяют вероятностный или статистический смысл волновой функции в квантовой механике.
Свойства
волновой функции. Если в качестве
области пространства в (3.3) взять
все пространство
Условие (3.4) называют условием нормировки волновой функции, а волновую функцию, удовлетворяющую этому условию, называют нормированной волновой функцией. 63.Боровская теория водородоподобного атома. Линейчатые спектры атомов. Постулаты Бора. Спектр атома водорода по Бору. Сериальная формула Линейчатый спектр атома представляет собой совокупность большого числа линий, разбросанных по всему спектру без всякого видимо-г о порядка. Постулаты: Атом может находиться только в особенных стационарных или квантовых состояниях, каждому из которых отвечает определенная энергия. В стационарном состоянии атом не излучает электромагнитных волн.
Электрон в атоме,
не теряя энергии, двигается по
определённым дискретным круговым
орбитам, для которых момент
импульса квантуется:
При
переходе электрона с орбиты
(энергетический уровень) на орбиту
излучается или поглощается квант энергии СПЕКТР АТОМА ВОДОРОДА ПО БОРУ: Постулаты, выдвинутые Бором, позволили рассчитать спектр атома водорода и водородоподобных систем - систем, состоящих из ядра с зарядом Ze и одного электрона (например, ионы Не+, Li2+), а также теоретически вычислить постоянную Ридберга. Следуя Бору, рассмотрим движение электрона в водородоподобной системе, ограничиваясь круговыми стационарными орбитами. Решая совместно уравнение (208.1) mev2/r = Ze2/(40r2), предложенное Резерфордом, и уравнение (210.1), получим выражение для радиуса n-й стационарной орбиты:
где n = 1, 2, 3, ... . Из выражения (212.1) следует, что радиусы орбит растут пропорционально квадратам целых чисел. Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде:
Стационарное уравнение Шрёдингера. Энергетический спектр. Квантовые числа. Структура электронных уровней. Правила отбора.
Энергетический спектр (закон дисперсии) — зависимость энергии частицы от импульса. Квантовые числа — энергетические параметры, определяющие состояние электрона и тип атомной орбитали, на которой он находится.
Структура
электронных уровней Согласно
квантовой теории атом обладает
определенными устойчивыми состояниями
с энергиями
Правила отбора – правила, которые на основе законов сохранения квантовых чисел устанавливают допустимые процессы с участием микросистем (молекул, атомов, ядер, элементарных частиц).
Физическая природа химической связи. Обменные взаимодействия Моле́кула (новолат. molecula, уменьшительное от лат. moles — масса[1]) — электрически нейтральная частица. Физический смысл — природа химической связи полностью определяется электрическим взаимодействием ядер и электронов. Чем больше связывающих электронов, тем меньше межъядерное расстояние и прочнее химическая связь между атомами углерода. Обменное взаимодействие бозонов и фермионов Для фермионов характер обменного взаимодействия обусловлен принципом Паули, согласно которому два фермиона не могут находиться в совершенно одинаковых состояниях. Для бозонов: чем больше бозонов находится в данном состоянии, тем с большей вероятностью в это состояние переходит ещё один бозон.
Энергетические зоны. Уровень Ферми. Деление твердых тел на проводники, полупроводники и диэлектрики. Электропроводность твердых тел. В твёрдом теле энергетический спектр состоит из отдельных разрешённых энергетических зон, разделённых зонами запрещённых энергий. При ширине уровня 1 эВ и количестве атомов в 1 см3, равном 1023 атомов/см3, расстояния между подуровнями чрезвычайно малы, и такую область можно рассматривать как энергетическую зону с квазинепрерывным спектром энергетических состояний. При положительной температуре Ферми-газ не будет являться вырожденным, и населённость уровней будет плавно уменьшаться от нижних уровней к верхним. В качестве уровня Ферми можно выбрать уровень, заполненный ровно наполовину (то есть вероятность находящегося на искомом уровне состояния быть заполненным частицей должна быть равна 1/2). В зависимости от степени заполнения валентной зоны электронами и ширины запрещенной зоны кристаллы подразделяются на металлы, полупроводники и диэлектрики. Согласно квантовой теории проводимость металлов
В проводимости участвуют не все электроны, а только те из них, которые имеют энергию вблизи уровня Ферми. Это – малая часть всех свободных электронов
Полупроводники р-типа, полупроводники n-типа. р-n переход. КОНТАКТНЫЕ ЯВЛЕНИЯ В ПОЛУПРОВОДНИКАХ - неравновесные электронные явления, возникающие при прохождении электрич. тока через контакт полупроводника с металлом или электролитом или через контакт двух различных полупроводников (гетеропереход)либо через границу двух областей одного и того же полупроводника с разным типом носителей заряда (см. р - п-переход)и разной их концентрацией. Полупроводник p-типа — полупроводник, в котором основными носителями заряда являются дырки. Полупроводники n-типа — полупроводник, в котором основные носители заряда — электроны проводимости. p-n-Перехо́д (n — negative — отрицательный, электронный, p — positive — положительный, дырочный), или электронно-дырочный переход — область пространства на стыке двухполупроводников p- и n-типа, в которой происходит переход от одного типа проводимости к другому. p-n-Переход является основой для полупроводниковых диодов, триодов и других электронных элементов с нелинейной вольт-амперной характеристикой.
Явление Зеебека. Явление Пельтье Эффект Зеебека — явление возникновения ЭДС в замкнутой электрической цепи, состоящей из последовательно соединённых разнородных проводников, контакты между которыми находятся при различных температурах. Эффект Пельтье — термоэлектрическое явление, при котором происходит выделение или поглощение тепла при прохождении электрического тока в месте контакта (спая) двух разнородных проводников.
Составные части атомного ядра (протоны и нейтроны). Изотопы. Атомные модели. Радиоактивность. Закон радиоактивного распада. Период полураспада, постоянная распада, среднее время жизни. А́томное ядро́ — центральная часть атома, в которой сосредоточена основная его масса (более 99,9 %).Атомное ядро состоит из нуклонов — положительно заряженных протонов и нейтральных нейтронов, которые связаны между собой при помощи сильного взаимодействия. Ядра с одинаковым числом протонов и разным числом нейтронов называются изотопами. В процессе развития физики выдвигались различные гипотезы строения атомного ядра, Атомные модели: Капельная модель ядра, Оболочечная модель ядра, Обобщённая модель Бора, Оптическая модель, Статистическая модель. Лишь небольшая часть нуклидов являются стабильными. В большинстве случаев ядерные силы оказываются неспособны обеспечить их постоянную целостность, и ядра рано или поздно распадаются. Это явление получило название радиоактивности. Существует несколько формулировок Закон радиоактивного распада., например, в виде дифференциального уравнения:
которое означает, что число распадов −dN, произошедшее за короткий интервал времени dt, пропорционально числу атомов N в образце.
Период
полураспада, среднее время
жизни
Поскольку
|




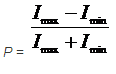
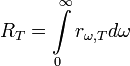 RЭ (интегральная
энергетическая светимость) -
энергетическая светимость определяет
количество энергии, излучаемой с
единичной поверхности за единицу
времени во всем интервале частот от
0 до ∞ при данной температуре Т.
RЭ (интегральная
энергетическая светимость) -
энергетическая светимость определяет
количество энергии, излучаемой с
единичной поверхности за единицу
времени во всем интервале частот от
0 до ∞ при данной температуре Т.
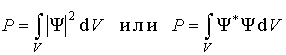 .
. (212.1)
(212.1)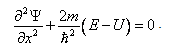 По
условию задачи (бесконечно высокие
«стенки»), частица не проникает за
пределы ямы, поэтому вероятность ее
обнаружения за пределами ямы равна
нулю. На границах ямы волновая функция
также должна обращаться в нуль.
По
условию задачи (бесконечно высокие
«стенки»), частица не проникает за
пределы ямы, поэтому вероятность ее
обнаружения за пределами ямы равна
нулю. На границах ямы волновая функция
также должна обращаться в нуль. 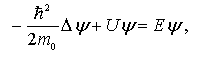 где
где 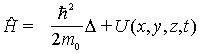 -
оператор полной энергии частицы
(оператор Гамильтона). Это уравнение
позволяет найти волновую функцию
-
оператор полной энергии частицы
(оператор Гамильтона). Это уравнение
позволяет найти волновую функцию 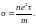
 время
релаксации.
время
релаксации.