33.Магнитное поле в вакууме

Источники магнитного поля. Индукция магнитного поля. Вихревой характер магнитного поля. Графическое изображение магнитных полей. Закон Био-Савара-Лапласа. Принцип суперпозиции. Индукция магнитного поля в центре кругового тока (вывод).

Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения[1], магнитная составляющая электромагнитного поля[2].

Магнитное поле создаётся током заряженных частиц, или изменяющимся во времени электрическим полем, или собственными магнитными моментами частиц .

Индукция магнитного поля-силовая характеристика магнитного поля. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью v .F=q[v x B] или F=qvBsina.

В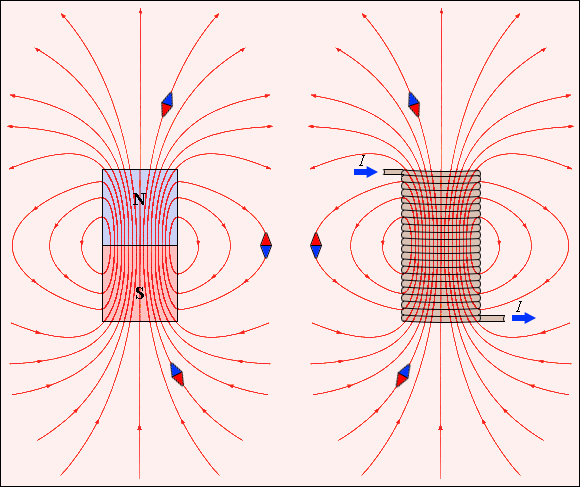 екторные поля, обладающие непрерывными линиями, получили название вихревых полей. Магнитное поле это вихревое поле.

З акон Био-Савара-Лапласа: Для тока текущего по контуру

Д ля распределенных токов

При́нцип суперпози́ции: результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.

Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя.

Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парных взаимодействий между всеми возможными парами частиц. В системе нет многочастичных взаимодействий.

Уравнения, описывающие поведение многочастичной системы, являются линейными по количеству частиц.

Индукция магнитного поля в центре кругового тока (вывод):

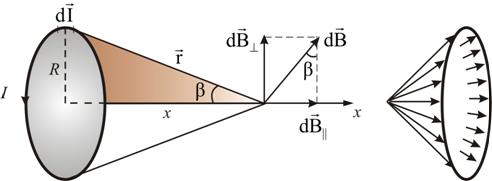Рассмотрим поле, создаваемое током I, текущим по тонкому проводу, имеющему форму окружности радиуса R.

Определим магнитную индукцию на оси проводника с током на расстоянии х от плоскости кругового тока. Векторы перпендикулярны плоскостям, проходящим через соответствующие dl и r. Следовательно, они образуют симметричный конический веер. Из соображения симметрии видно, что результирующий вектор B направлен вдоль оси кругового тока. Каждый из векторов Db вносит вклад равный dB паралл. ,а dB перп. взаимно уничтожаются. Но , , а т.к. угол между dl и r α – прямой, то тогда получим

,

Подставив в формулу и, проинтегрировав по всему контуру , получим выражение для нахождения магнитной индукции кругового тока:

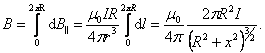
При x=0 , получим магнитную индукцию в центре кругового тока:

34. Движение заряженных частиц в магнитном поле.

Сила Лоренца. Величина и направление силы. Движение заряженных частиц в магнитном поле в зависимости от угла между вектором скорости и вектором магнитной индукции поля. Вывод формулы для радиуса кривизны траектории. Работа силы Лоренца.

Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью v заряд q лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще[1], иначе говоря, со стороны электрического E и магнитного B полей. Выражается как:

или F=qvBsina

Eсли левую руку расположить так, чтобы составляющая магнитной индукции В, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены против движения отрицательного заряда, то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца F л.

1. Заряженная частица влетает в магнитное поле со скоростью , направленной вдоль поля или противоположно направлению магнитной индукции поля .

В этих случаях сила Лоренца = 0 и частица будет продолжать двигаться равномерно прямолинейно.

2. Заряженная частица движется перпендикулярно линиям магнитной индукции тогда сила Лоренца F=qvb , следовательно, и сообщаемое ускорение будут постоянны по модулю и перпендикулярны к скорости частицы. В результате частица будет двигаться по окружности, радиус которой можно найти на основании второго закона Ньютона

3. Скорость заряженной частицы направлена под углом к вектору.

Движение частицы можно представить в виде суперпозиции равномерного прямолинейного движения вдоль поля со скоростью и движения по окружности с постоянной по модулю скоростью в плоскости, перпендикулярной полю.

радиус аналогично предыдущему, только v нужно заменить на vsina.

Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны.