10. Метод знаходження екстремуму функції багатьох змінних кроки (етапи) цього методу.
Методи пошуку екстремумів функцій поділяються на градієнтні і безградієнтні за наступною ознакою: градієнтні основані на обчисленні й аналізі часткових похідних функції , безградієнтні не використовують значень похідних.
Метод координатного спуску
Рух від початкової точки у напрямку однієї з осей координат до моменту початку зростання цільової функції, перехід до напрямку іншої осі і т.д., поки не буде досягнута точка, рух з якої по будь осі координат з мінімально можливим кроком призводить до збільшення значення цільової функції.
Основні етапи пошуку екстремуму методом координатного спуску:
1) вибір
початкового наближення
;
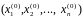2) вибір напрямку пошуку, тобто номери i(1,2,...,n) компоненти вектора (x1,x2,...,xn), яка буде змінюватися;
3)
обчислення значення похідної цільової
функції за обраним аргументу
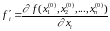(якщо
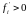, то з ростом xi
значення
f
(х1,
х2,...,
хn)
збільшується, а якщо
,
то зменшується);
4) зміна значення х1,х2,...,хn у відповідності з виразом
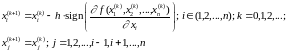
до тих пір, поки f (х1(k+1),х2(k+1),...,хn(k+1)) < f (х1(k),х2(k),...,хn(k)); в противному випадку виконується повернення на п. 2) у вибір наступного напрямку пошуку, при цьому x i (0)=x i(k), i=1,2,...n (h – крок пошуку, sign(z) – знак виразу (z);
5) якщо спроба руху з кроком h в будь-якому з n можливих напрямків призводить до ситуації f (х1(k+1),х2(k+1),...,хn(k+1)) f (х1(k), х2(k),...,хn(k)), то здійснюється дроблення кроку: h = h/p (p > 1) і знову виконується п. 4);
6) пошук вважається закінченим, коли значення h стає менше заданої точності .
11. Поняття градієнта функції багатьох змінних та його інтерпритація
Градієнт функції f (x1,x2,...,xn) в точці (x1(0),x2(0),...,xn(0)) це вектор, довжина якого
характеризує швидкість зростання функції в цій точці, а напрямок відповідає напрямку якнайшвидшого зростання функції. Антиградієнт – це вектор такої ж довжини, спрямований у протилежний бік (рис. 10.1)
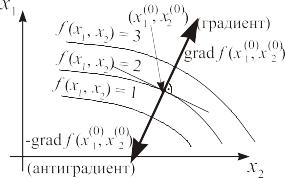
Рисунок 2.10 Градієнт и антиградієнт функції f (x1, x2)
12. Використання градієнта функції для знаходження екстремуму функції
Ідея методу: Кожна наступна точка пошуку min (кожен новий член мінімалізує послідовності) виходить в результаті переміщення з попередньої точки у напрямку антиградієнта цільової функції. Якщо в результаті цього переміщення спостерігається збільшення значення цільової функції, то значення робочого кроку пошуку h зменшується. Пошук припиняється, коли виконується необхідна умова ext , наприклад довжина градієнта стає менше необхідної точності:
,
(12.1)
або менше необхідної точності стає величина кроку пошуку
h . (12.2)
Розрізняють методи градієнта з перемінним кроком і з постійним кроком (малюнок 12.1). При використанні методу градієнта з перемінним кроком зміна значень x1, x2, ..., xn проводиться відповідно до виразу
,
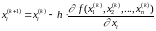i=1,2,...,n
, k=0,1,2…,
(12.3)
а зупинка пошуку - при виконанні нерівності (12.1). При виникненні ситуації f (х1(k+1),х2(k+1),...,хn(k+1)) f (х1(k), х2(k),..., хn(k)) значення h зменшується, наприклад ділиться на число р > 1. Характер зміни значений x1,x2,...,xn згідно (12.3) залежить від величини і знака відповідних приватних похідних цільової функції. У міру наближення до точки min абсолютні величини приватних похідних зменшуються, отже і крок пошуку є змінним - зменшується у міру наближення до шуканої точці. Такий характер пошуку вимагає іноді досить значних витрат часу
.
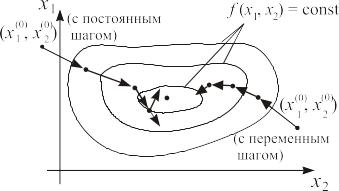
Рис. 12.1
Застосування методу градієнта з постійним кроком дозволяє скоротити витрати часу, але вимагає дещо більшого обсягу обчислень при зміні значень аргументів цільової функції. Його основне співвідношення:
,
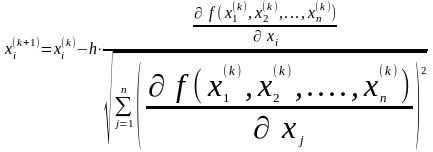i=1,2,...,n;
k=0,1,2,...
, (12.4)
тобто. Відстань між точками (x1(k),x2(k),...,xn(k)) и (x1(k+1),x2(k+1),...,xn(k+1)) рівна
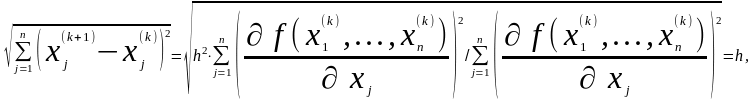отже
величина кроку пошуку в даному випадку
постійна і дорівнює обраному значенням
h. Якщо зміна аргументів цільової функції
відповідно до (2.8) приводить до збільшення
її значення, крок пошуку зменшується.
Останов пошуку min
за методом градієнта з постійним кроком
здійснюється при виконанні нерівності
(12.2).