6. Суть рівняння в задачі знаходження екстремуму функції

Суть полягає в тому, щоб найти критичні точки функції 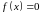, тобто точки, що належать області визначення функції, в яких похідна 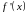перетворюється на нуль або не існує.

Що дозволить дослідити характер зміни функції і знак похідної у проміжках, на які знайдені критичні точки ділять область визначення функції .

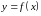Критична точка 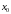є точка мінімуму, якщо вона відокремлює проміжок, в якому 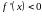, від проміжку, в якому 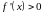, і точка максимуму – в іншому випадку. Якщо ж у сусідніх проміжках, розділених критичною точкою , знак похідної не змінюється, то в точці функція екстремуму не має.

7. Числовий метод Ньютона знаходження екстремуму функції однієї змінної.

Метод Ньютона заснований на квадратичній апроксимації функції, що мінімізується в околі точки 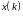. Мінімум квадратичної функції легко знайти, прирівнюючи її градієнт нулю. Можна відразу ж обчислити положення екстремуму і вибрати його в якості наступного наближення до точки мінімуму.

Послідовність обчислень для реалізації алгоритму:

1. задати (довільно) точку початкового наближення ;

2. в циклі за номером ітерації k = 0, 1, ... обчислити:

• значення вектора градієнта 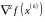в точці 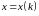за формулою:

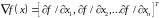
• значення матриці других похідних за формулою:

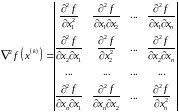
• значення матриці зворотної матриці других похідних ;

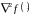• значення кроку 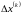за формулою:

• нове значення наближення 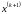за формулою (2) :

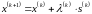
3. закінчити ітераційний процес, використовуючи одну з умов, описаних у п 1.5.

Переваги методу Ньютона:

• якщо мінімізувати функція є квадратичною, то метод дозволить знайти мінімум за один крок;

• якщо мінімізована функція належить до класу поверхонь обертання (тобто володіє симетрією), то метод також забезпечує збіжність за один крок (оскільки в точці мінімуму аргументи функції, що мінімізується і її квадратичної апроксимації збігаються);

• якщо функція несиметрична, то метод не забезпечує збіжність за кінцеве число кроків. Але для багатьох функцій (навіть дуже складних, наприклад, для функції Розенброка, яка буде досліджуватися Вами в ході лабораторної роботи) досягається набагато більш висока швидкість збіжності, ніж при використанні інших модифікацій методу найшвидшого спуску.

Недоліки методу

Ньютона пов'язані з необхідністю обчислень і (головне!) звернення матриць других похідних. При цьому не тільки витрачається машинний час, але (це істотніше) можуть з'явитися значні обчислювальні похибки, якщо матриця виявиться погано обумовленою (тобто значення визначника цієї матриці буде близько до нуля).

8. Метод «вилки» знаходження екстремуму функції однієї змінної

Його суть полягає в побудові послідовності вкладених відрізків, що містять корінь. При цьому на кожному кроці черговий відрізок ділиться навпіл і в якості наступного відрізка береться та половина, на якій значення функції в кінцях мають різні знаки. Процес продовжують до тих пір, поки довжина чергового відрізка не буде менше, ніж величина 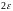. Тоді його середина і буде наближеним значенням кореня з точністю .

Алгоритм даного методу можна записати так:

1.ввесті дані (a, b, ).

2.Якщо потрібна точність досягнута (| b - a | < ) то перейти до п.6

3.Взяти середину чергового відрізка (С = (a + b) / 2).

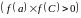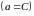4. Якщо значення функції в точках а і С одного знака , то в якості наступного відрізка взяти праву половину , інакше ліву ( ).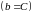

5.Перейти до п.2.

6.Відповідь ((a + b) / 2).