1. Аксиомы статики

Статика- раздел механики, который изучает условия равновесия твердых тел под влиянием приложенных к ним сил.

Аксиомы статики:

1) Принцип инерции. Под действием уравновешенной системы сил, абсолютно твердое тело или материальная точка находятся в равновесии или движутся равномерно и прямолинейно. 2) Условия равновесия сил. Две силы равные по модулю и направленные по одной прямой в разные стороны уравновешиваются. |F₁|=|F₂| 3) Принцип присоединения. Не нарушая механического состояния тела к нему можно добавить или убрать уравновешенную систему сил. |F₁|=|F₂|; |F₃|=|F₄|. Следствие из 2 и 3 аксиом. Силу действующую на твердое тело можно перемещать вдоль линии её действия.

4) Правила параллелограмма. Равнодействующая двух сил, приложенных в одной точке, приложена в этой же точке и является диагональю параллелограмма построенного на этих силах, как на сторонах. |F₁|=|F₂|=|F₃|;

F₀ →+ (F₂; А₃)

- (F₁; F₂)

5) Закон действия и противодействия. При взаимодействии материальных тел всякому действию есть равное и противоположно направленное противодействие. |F₁|=|F₂|

2. Связи и реакции связей

Все тела делятся на: свободные (перемещение не ограничено)

и связанные (перемещение которых ограничено другими телами(связи))

Силы, действующие от связей и препятствующие перемещению, называют реакциями связей.

Принцип освобождения от связи. Всякое связанное тело можно представить свободным, если связи заменить их реакциями.

Типы связи:

1) В вид жесткого прямого стержня с шарнирным закреплением концов.

[R]- реакция.

Реакции, направленные вдоль стержня, могут быть растянутыми или сжатыми.

2) Связь, осуществляемая ребром двугранного угла и точечной опоры.

3) Гибкая связь (веревка, трос, цепь).

4) Связь в виде гладкой плоскости.

5) В виде шероховатой плоскости.

3. Проекция силы на ось.

Проекция силы на ось равна произведению модуля этой силы на косинус угла между силой и положительным направлением оси.

4. Условия равновесия плоской системы сходящихся сил: геометрическая и аналитическая форма.

Условия и уравнения плоской системы сходящихся сил.

Плоская система сил будет находиться в равновесии, если их равнодействующая будет равна 0 (F_∑=0)

Формула равн. необходимо и достаточно, чтобы силовой многоугольник, построенный для данной системы сил, был замкнутый.

Аналитическая форма имеет два уравнения равновесия: (1 Е F_x=0) (E F_y =0). Алгебраическая сумма проекции всех сил на ось иксов должна быть равна нулю и на ось игрик тоже должна быть равна нулю.

5. Плечо и момент силы относительно точки, правило знаков.

Теорема Пуансо о параллельном переносе сил. Не изменяя действия силы на тело, её можно перенести параллельно по своему начальному направлению в любую точку тела, присоединяя при этом некоторую пару. |F|=|F’|=|F”|.

F’

(F, F”)

Главный момент данной плоской системы сил- это сумма моментов всех сил относительно какой-либо точки о. (М гл.)

М гл.=∑М₀ (F)

6 .Плечо и момент силы относительно оси , правило знаков плече - кротчайшее расстояние между линиями сил.момент силы наз вращательное усилие создаваемое вектором силы относительно другого объекта. момент пары сил будет считаться положительным если пара стремится сообщить ему вращательное движение по часовой стрелке ,если против будет считаться отрицательным. 8 вопрос : статическая- не меняется со временем или меняется очень медленно динамическая- меняется значение в короткий промежуток времени вызывает большие силы инерции может привести к внезапному разрушению  повторно переменные - многократно меняет значение и знаки 7. Условие и уравнения равновесия произвольной плоской системы сил.

это сис-ма ,когда линии действия сил лежат в одной плоскости и расположены в произвольном порядке.  теорема пуансо: не изменяя действия силы на тело ,её можно переместить параллельно своему начальному направлению в любую точку тела, присоединяя при этом некоторую пару 8. Классификация нагрузок. статическая- не меняется со временем или меняется очень медленно динамическая- меняется значение в короткий промежуток времени вызывает большие силы инерции может привести к внезапному разрушению  повторно переменные - многократно меняет значение и знаки 9 .Опорные устройства балочных систем. шарнирно- подвижная опора шарнирно - неподвижная опора жестко - защемленная опора 10 .Пространственная система сходящихся сил . Условия и уравнения равновесия. пространственная сис- ма сходящихся сил : линии действия сил пересекаются в одной точке ,но не лежат в одной плоскости.  условия равновесия в аналитической форме :  1 Fx= 0 2 Fy=0 3 Fz=0 геометр. форма : необходимо и достаточно ,чтобы силовой многоугольник ,построенный для этой сис-мы сил был замкнутым. 11.Момент силы относительно оси. Момент силы относительно оси равен моменту проекции этой силы на плоскость перпендикулярной данной оси относительно точки пересечения оси с плоскостью. Знак определяется с помощью положительного направления оси , если по часовой стрелке то - , если по часовой стрелке то + . Следствие : 1. Момент не изменяется при переносе силы вдоль линии её действия. 2. Момент силы относительно оси равен 0 если сила и ось лежат в одной плоскости .

12.Условия равновесия системы сил произвольно расположенных в пространстве. Условия равновесия : Для равновесия произвольной плоской системы необходимо и достаточно, чтобы сумма моментов относительно двух произвольно взятых точек тела была равна нулю и сумма проекций сил на одну из осей коpординат была равна нулю.

аналитическая форма равновесия : 1.Fx = 0 4. Mx(F) = 0 2.Fy = 0 5. My(F) = 0 3.Fz = 0 6. M2(F) = 0 13.Положение центра тяжести простых геометрических фигур.

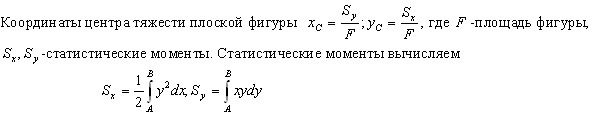
Точка приложения силы тяжести : Для определения точки приложения силы тяжести (равнодействующей параллельных сил) используем теорему Вариньона о моменте равнодействующей:

Момент равнодействующей относительно оси равен алгебраической сумме моментов сил системы относительно этой оси. 14. Виды движений в зависимости от ускорений. Различают следующие виды движения точки в зависимости от ускорения: 1. Прямолинейное движение. В этом случае траектория движения точки – прямая, причем точка движется вдоль этой прямой в одном направлении. Радиус кривизны прямой R равен бесконечности (прямую можно считать окружностью бесконечно большого радиуса). 2. Равномерное криволинейное движение. Так как при равномерном движении точки модуль скорости остается постоянным, то есть v = const 3. Равномерное прямолинейное движение 4. Равнопеременное криволинейное движение. Равнопеременным называется такое криволинейное движение точки, при котором касательное ускорение остается все время величиной постоянной 15. Линейные скорости и ускорения точек вращающегося тела. Если тело вращается вокруг оси, то его точки перемещаются по окружностям , радиусы которых r равны расстояниям точек от оси вращения. Касательное и нормальное ускорения при вращательном движении твердого тела также называют соответственно вращательным и центростремительным. - Касательное ускорение точки вращающегося тела определяется из выражения

- Нормальное ускорение точки равно отношению квадрата ско­рости к радиусу окружности

Значение полного ускорения вычисляется как диагональ пря­моугольника, построенного на составляющих ускорениях At, и An . Подставив значения касательного и нормального ускорений, получим