Регистрационное кодирование

Регистрационное кодирование используется для однозначной идентификации объектов и не требует предварительной классификации объектов. Различают порядковую и серийно-порядковую систему.

Порядковая система кодирования предполагает последовательную нумерацию объектов числами натурального ряда. Этот порядок может быть случайным или определяться после предварительного упорядочения объектов, например по алфавиту. Этот метод применяется в том случае, когда количество объектов невелико, например кодирование названий факультетов университета, кодирование студентов в учебной группе.

Серийно-порядковая система кодирования предусматривает предварительное выделение групп объектов, которые составляют серию, а затем в каждой серии производится порядковая нумерация объектов. Каждая серия также будет иметь порядковую нумерацию. По своей сути серийно-порядковая система является смешанной: классифицирующей и идентифицирующей. Применяется тогда, когда количество групп невелико.

10. Сущность и назначение машинных кодов – прямой, дополнительный, обратный.

В ЭВМ все арифметические операции сводятся к сложению и сдвигу чисел влево или вправо. При этом учитываются знаки чисел, определяющие знак результата и факт наличия и отсутствия переполнения разрядной сетки.

Замена вычитания на сложение может проводиться с помощью дополнительного и обратного кода. Их суть состоит в том, что отрицательное слагаемое представляется в виде дополнения до некоторой константы K, такой, что K-B>0. Обратный и дополнительный коды отличаются выбором этой константы.

С = A – B = A + (-B) = A + (10ⁿ - B) – Bⁿ = A + (10ⁿ – 1 - B) – 10ⁿ + 1, где 10 – основание системы счисления, 10ⁿ – const при введении дополнительного, (10ⁿ-1) – const обратного кода, n – количество разрядов представления целых чисел в данной системе счисления.

Из полученной суммы необходимо изъять добавленную константу.

Пример.

59|2 1 59₁₀ = 00111011₂

29|2 1

14|2 0

7|2 1

3|2 1

1

K_доп = 100000000 00111011

-00111011 +11000100

11000101 +1

11000101

59₁₀ = 00111011₂ ПК

11000100₂ ДК

С=59-34 K_доп = 10² = 100 -34 = 66_доп

59

+66

125 – 100 = 25

K_обр = 10² – 1 = 99 -34 = 65_обр

59

+65

124 –100 = 24

+1

25

В случае дополнительного кода его константа компенсируется ликвидацией единицы переноса из старшего разряда. А в случае обратного кода – ликвидацией единицы и прибавления её к результату, то есть на одну операцию больше. Поэтому для реального вычитания используется дополнительный код, а обратный используется для получения дополнительного.

A₁₀ = 00111011₂ B₁₀ = -34 = -00100010₂

K_доп = 2⁸ = 100000000₂

A_доп = 100000000 B_доп = 100000000

-00111011 -0100010

11000101 11011110

С₁ = А – В A_пр = 00111011 B_доп = 11011110

00111011

+11011110

1)00011001

С₂ = B – A B_пр = 00100010 A_доп = 11000101

00100010 100000000

+11000101 -11100111

11100111 |00011001| - модуль результата

При сложении чисел с разными знаками единица переноса из старшего разряда является признаком положительного результата, отсутствие переноса – признаком отрицательного результата. При этом код результата находится в дополнительном коде. Чтобы получить его модуль, необходимо скомпенсировать константу дополнительного кода.

С₂ = A + B A_пр = 00111011 B_пр = 00100010

00111011

+00100010

*)01011101₂ = 93₁₀ *) – отсутствует

С₃ = -A – B A_доп = 11000101 B_доп = 11011110

11000101 100000000

+11011110 -10100011

1)10100011 |001011101|

При сложении чисел с одинаковыми знаками признаки противоположны. При сложении положительных чисел признаком положительного результата является отсутствие переноса из старшего разряда, признаком отрицательного результата – его наличие. Эти же признаки говорят об отсутствии переполнения разрядной сетки.

B_пр = 200 = 11001000₂

B_доп = 100000000

11001000

00111000

D₁ = A + B A_пр = 00111011 B_пр = 11001000

00111011

+11001000

1)00000011

D₂ = -A – B -A_доп = 11000101 -B_доп = 00111000

11000101 100000000

+00111000 -11111101

*)11111101 00000011

Правила построения дополнительного и обратного кода на примере чисел 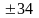. Старший бит отведён под знак числа.

10
+34	00100010	00100010	00100010
-34	1.0100010	11111111 -00100010	100000000 -00100010

1. Прямой код положительного и отрицательного числа отличаются только знаковыми разрядами.

2. Прямой, дополнительный и обратный коды положительных чисел совпадают.

3. Обратный код отрицательного числа образуется из прямого кода положительного числа путём инверсии кода, включая знаковый разряд.

4. Дополнительный код отрицательного числа образуется дополнением единицы к младшему разряду обратного кода или путём инверсии прямого кода, исключая последнюю единицу и следующие за ней нули.

Числа в естественной форме хранятся в ЭВМ в дополнительном коде, в нормальной форме – в прямом коде.