Вопрос 12

Система счисле́ния — символический метод записи чисел, представление чисел с помощью письменных знаков.

Система счисления:

даёт представления множества чисел (целых и/или вещественных);

даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление);

отражает алгебраическую и арифметическую структуру чисел.

1)Чтобы перевести целое число из одной системы счисления с основанием d1 в другую с основанием d2 необходимо последовательно делить это число и получаемые частные на основание d2 новой системы до тех пор, пока не получится частное меньше основания d2. Последнее частное – старшая цифра числа в новой системе счисления с основанием d2, а следующие за ней цифры - это остатки от деления, записываемые в последовательности, обратной их получению. Арифметические действия выполнять в той системе счисления, в которой записано переводимое число.

2)Чтобы перевести правильную дробь из системы счисления с основанием d1 в систему с основанием d2, необходимо последовательно умножать исходную дробь и дробные части получающихся произведений на основание новой системы счисления d2. Правильная дробь числа в новой системе счисления с основанием d2 формируется в виде целых частей получающихся произведений, начиная с первого.

Если при переводе получается дробь в виде бесконечного или расходящегося ряда, процесс можно закончить при достижении необходимой точности.

3)При переводе смешанных чисел, необходимо в новую систему перевести отдельно целую и дробную части по правилам перевода целых чисел и правильных дробей, а затем оба результата объединить в одно смешанное число в новой системе счисления.

Для перевода числа P-ичной системы в десятичную необходимо использовать следующую формулу разложения:

аnan-1…а1а0=аnPn+ аn-1Pn-1+…+ а1P+a0 .

Наиболее употребляемыми в настоящее время позиционными системами являются:

1 — единичная[1] (счёт на пальцах, зарубки, узелки «на память» и др.);

2 — двоичная (в дискретной математике, информатике, программировании);

3 — троичная;

8 — восьмеричная;

10 — десятичная (используется повсеместно);

12 — двенадцатеричная (счёт дюжинами);

16 — шестнадцатеричная (используется в программировании, информатике);

60 — шестидесятеричная (единицы измерения времени, измерение углов и, в частности, координат, долготы и широты).

Вопрос 13

Mathcad является математическим редактором, позволяющим проводить разнообразные научные и инженерные расчеты, начиная от элементарной арифметики и заканчивая сложными реализациями численных методов. Пользователи Mathcad — это студенты, ученые, инженеры, разнообразные технические специалисты. Благодаря простоте применения, наглядности математических действий, обширной библиотеке встроенных функций и численных методов, возможности символьных вычислений, а также превосходному аппарату представления результатов (графики самых разных типов, мощных средств подготовки печатных документов и Web-страниц), Mathcad стал наиболее популярным математическим приложением.

Основные инструменты математика — это операции с переменными величинами и функциями. В Mathcad переменные, операторы и функции реализованы в интуитивной форме, т. е. выражения в редакторе вводятся и вычисляются так, как они были бы написаны на листе бумаги. Порядок вычислений в документе Mathcad также очевиден: математические выражения и действия воспринимаются процессором слева направо и сверху вниз.

Символьный вывод и численный вывод

Наряду с численным выводом, в Mathcad имеется возможность символьного, или аналитического, вычисления значения выражения. Для символьных вычислений имеется ряд специальных средств, которые будут детально рассмотрены позднее (см. гл. 5), самое простое из них — это оператор символьного вывода (symbolic evaluation). Он обозначается символом -» и в большинстве случаев применяется точно так же, как оператор численного вывода, однако внутреннее различие между действием этих двух операторов огромно. Если численный вывод — это в обычном смысле этого слова "запрограммированный" расчет по формулам и численным методам, скрытый от глаза пользователя, то символьный вывод — результат работы системы искусственного интеллекта, встроенной в Mathcad и называемой символьным процессором. Работа символьного процессора также невидима (и, чаще всего, даже трудно представима) пользователю и заключается в анализе самого текста математических выражений. Конечно, гораздо более узкий круг формул можно рассчитать символьно, хотя бы потому, что, вообще говоря, относительно не такая большая часть математических задач допускает аналитическое решение.

Чтобы попытаться вычислить символьно математическое выражение, например В • sin(arcsin(С • Х)), где В,С,Х — некоторые переменные:

Введите это выражение: В • sin(asin(С • Х)).

Введите оператор символьного вывода сочетанием клавиш <Ctrl>+<>, либо нажатием соответствующей кнопки (рис. 3.4) на панели Symbolic (Символика) или Evaluation (Выражения).

Точно так же, как рассчитываются численно значения функций, можно вычислять их и с помощью символьного процессора. Сравните соответствующие результаты, которые представлены в листинге 3.12 (конечно, символьный и численный ответы равны: 9•cos(8)=-1.31). Аналогично можно "символьно выводить значения переменных. Например, присвоить некоторой переменной значение функции или сложного выражения (листинг 3.13, вторая строка) и затем вывести значение переменной в символьном виде.

Листинг 3.12. Численный и символьный вывод значения функции

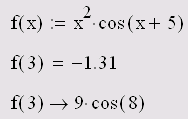
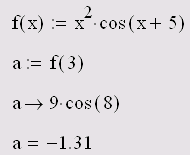
Как показывают приведенные примеры, преимущество символьных вычислений заключается в выдаче аналитического результата, который для математика часто является более ценным. Поэтому, исходя из специфики конкретных задач, решайте, стоит ли наряду с численными расчетами попытаться получить и символьное решение.