34.Параметры зубчатого зацепления. Качественные показатели зубчатого зацепления.

1. Делительными окружностя ми пары зубчатых колес называ ются соприкасающиеся окружно сти, катящиеся одна по другой без скольжения. Эти окружности, на ходясь в зацеплении (в передаче), являются сопряженными. На чер тежах диаметр делительной ок ружности обозначают буквой d.

2. Окружной шаг зубьев Рt — расстояние (мм) между одноимен ными профильными поверхностя ми соседних зубьев. Шаг зубьев, как нетрудно представить, равен делительной окружности, разде ленной на число зубьев z.

3. Длина делительной окруж ности. Модуль. Длину делитель ной окружности можно выразить через диаметр и число зубьев: Пd = Pt • r. Отсюда диаметр делитель ной окружности d = (Рt • z)/П.

Отношение Pt/П называется модулем зубчатого зацепления и обозначается буквой т. Тогда диаметр дели тельной окружности можно выразить через модуль и число зубьев d = m • z. Отсюда m = d/z.

Значение модулей для всех передач — вели чина стандартизированная.

Для понимания зависимости между вели чинами Рt т и d приведена схема на рис. 178, II, где условно показано размещение всех зубь ев 2 колеса по диаметру ее делительной окруж ности в виде зубчатой рейки.

4. Высота делительной головки зуба ha — расстояние между делительной окружностью колеса и окружностью вершин зубьев.

5. Высота делительной ножки зуба hf — расстояние между делительной окружностью колеса и окружностью впадин.

6. Высота зуба h — расстояние между ок ружностями вершин зубьев и впадин цилинд рического зубчатого колеса h = ha + hf..

7. Диаметр окружности вершин зубьев da — диаметр окружности, ограничивающей вершины головок зубьев.

8. Диаметр окружности впадин зубьев df — диаметр окружности, прохо дящей через основания впадин зубьев. Одним из качественных показателей зубчатой передачи является коэффициент перекрытия  , равный  , где рв – шаг по основной окружности (расстояние между одноимёнными точками

34. Продолжение

двух соседних зубьев, замеренное по дуге основной окружности). Коэффициент  показывает сколько пар зубьев в среднем одновременно находится в зацеплении. Для прямозубой передачи обычно  . Чем больше  , тем более плавно и бесшумно работает передача.  Другим качественным показателем является коэффициент скольжения, который учитывает влияние геометрии передачи и её кинематики на скольжение и износ профилей, скользящих друг по другу (рис. 74), что видно из картины скоростей. На этой картине: - скорость точки к первого колеса; - проекция этой скорости на касательную к контактирующим п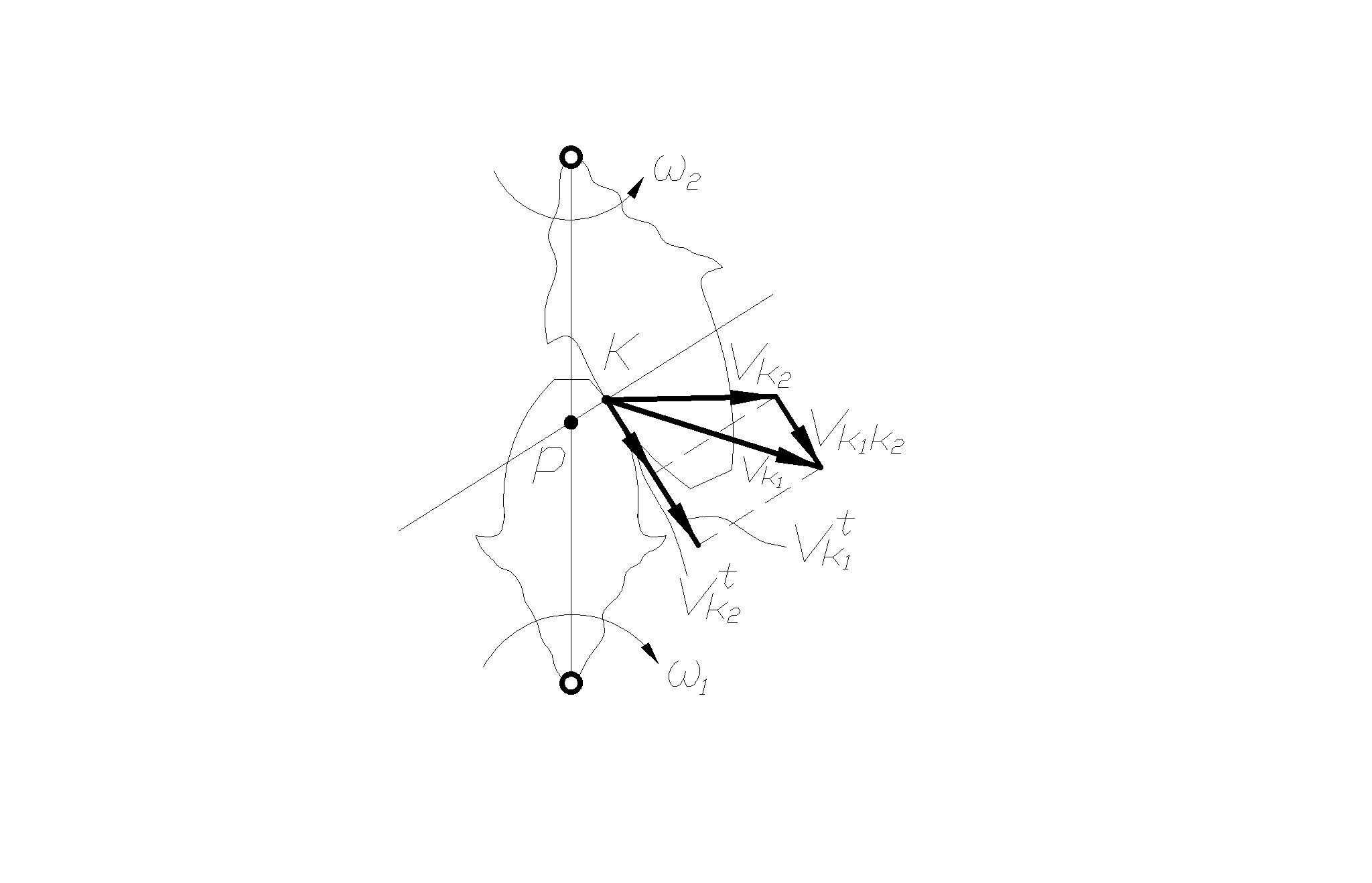 рофилям;  и   - тоже для колеса 2. Скорость скольжения колеса 1 и 2 относительно друг друга равна: . Коэффициенты скольжения колёс 1 и 2 равны: 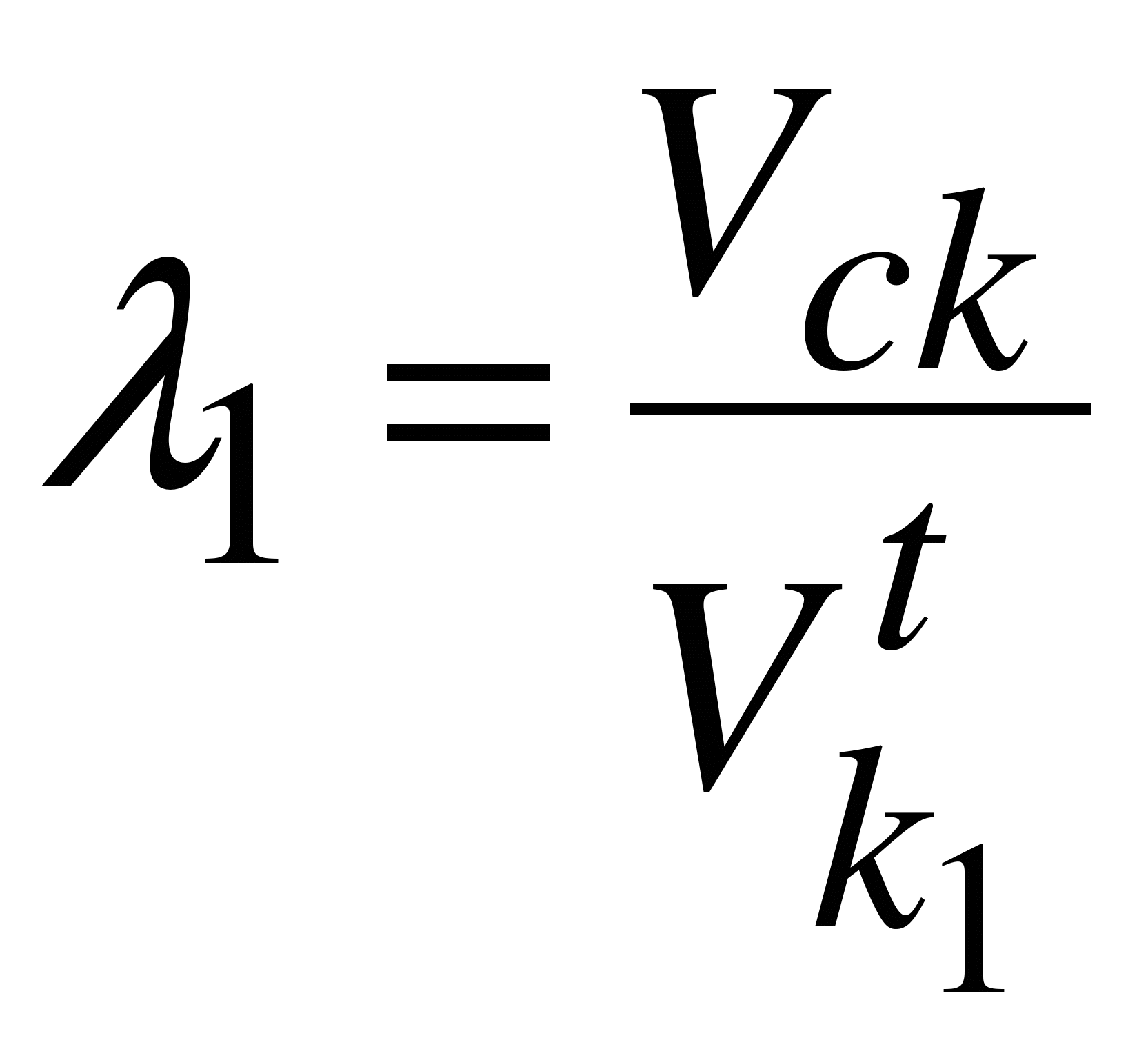;  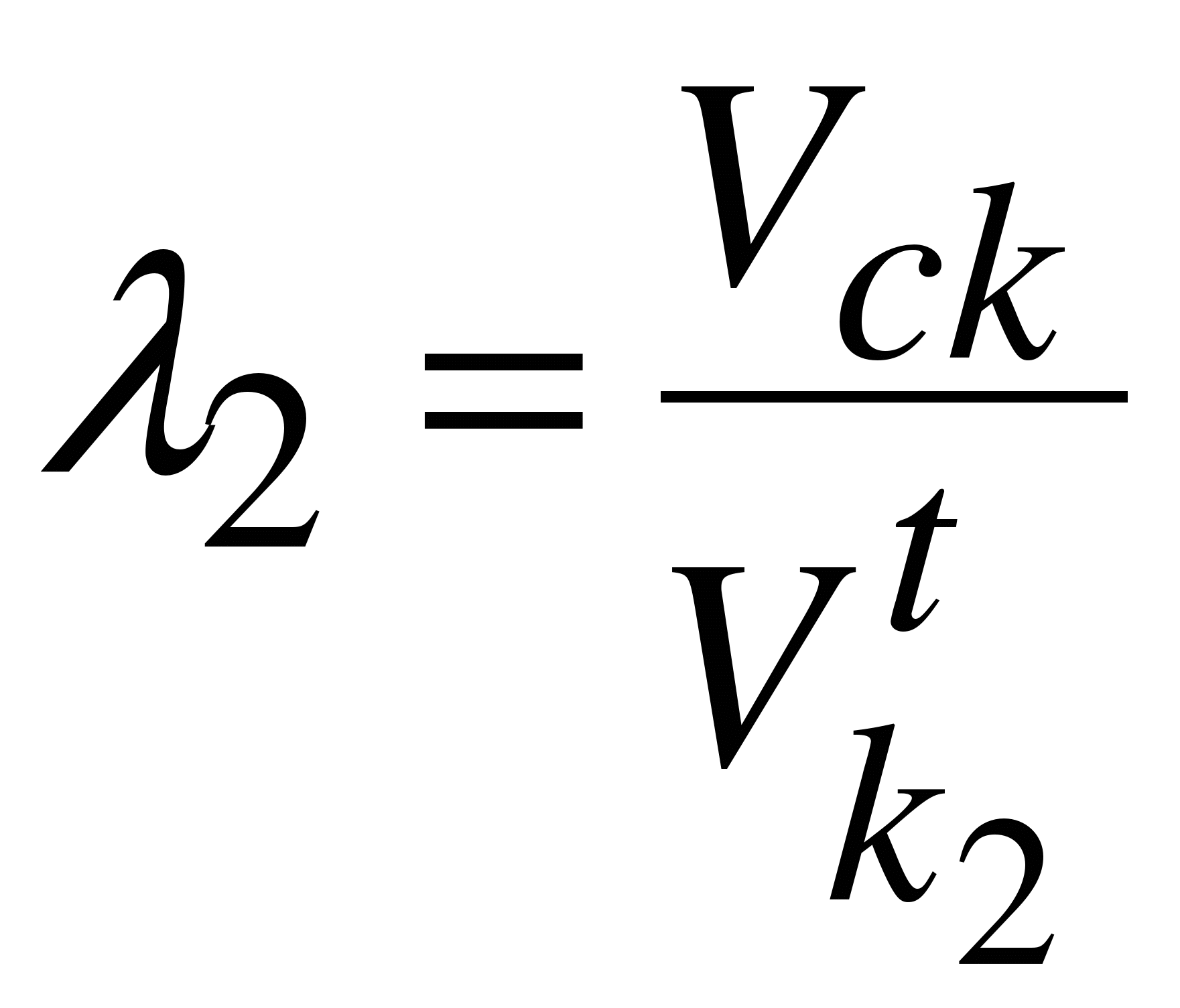. Эти коэффициенты равны нулю в полюсе (точка Р) и увеличиваются с удалением от него по линии зацепления. 

Таким образом, чем длиннее линия зацепления, (то есть, чем больше коэффициент перекрытия  ), тем больше скольжение и износ профилей зубьев.

35. 36 Смещение режущего инструмента при нарезании зубчатого колеса. Заострение зуба при смещении

При нарезании колёс режущий инструмент можно располагать ближе к заготовке или дальше от неё. Положение инструмента определяется расстоянием между делительной окружностью колеса и так называемой модульной прямой рейки, проходящей через середину высоты зуба режущего инструмента. В зависимости от положения рейки по делительной окружности может перекатываться без скольжения либо модульная прямая рейки, либо начальная прямая, отстоящая от модульной прямой на величину смещения “b”, которое называется сдвигом или коррекцией, а коэффициент χ (хи), равный χ=b/m, называется коэффициентом смещения инструмента. Если инструмент смещён от нарезаемого колеса, то χ считается положительным (положительная коррекция), а если – к центру колеса, то χ отрицателен (отрицательная коррекция). При χ=0 нарезаемое колесо называется нормальным (нулевым). Толщина зуба и ширина впадины такого колеса по делительной окружности равны. При положительной коррекции увеличивается прочность зуба, но уменьшается длина линии зацепления, а следовательно и коэффициент перекрытия  . При отрицательной коррекции – обратный эффект, т. е. увеличивается плавность и бесшумность работы передачи, но прочность зуба уменьшается. Зацепление двух зубчатых колёс характеризуется суммарным коэффициентом коррекции χΣ=χ1+χ2, причём возможны три случая: 1) χΣ=0 при χ1=χ2=0, когда в зацеплении находятся два нулевых зубчатых колеса (нулевое зацепление); 2) χΣ=0 при χ1=-χ2, когда в зацеплении находятся два корригированных зубчатых колеса, коэффициенты коррекции которых равны по величине и противоположны по знаку (равносмещённое зацепление с высотной коррекцией); 3) χΣ≠0, когда в зацеплении находятся два корригированных колеса, имеющих: а) χΣ>0 – положительное неравносмещённое зацепление с угловой коррекцией;

35, 36. ПРОДОЛЖЕНИЕ б) χΣ<0 - отрицательное неравносмещённое зацепление с угловой коррекцией. В первых двух случаях (χΣ=0) делительные окружности совпадают с начальными, угол зацепления   равен углу исходного контура рейки   и межосевое расстояние равно  , в отличие от неравносмещённого зацепления, где делительные и начальные окружности не совпадают,  ≠ , а межосевое расстояние равно:  , с учётом того, что   при  ;   и  ;  . При нарезании нулевых колёс с малым числом зубьев может возникнуть явление врезания головок зубьев режущего инструмента в ножки зубьев колеса. Это явление называется подрезанием зуба. При этом уменьшается его прочность и увеличивается износ рабочей части зуба (рис. 79). Согласно свойствам эвольвентного зацепления точки контакта зубьев эвольвентного профиля совпадают с линией NP, начиная с точки N, то есть высота прямолинейной части головки зуба режущего

инструмента (рейки) должна быть меньше отрезка PF, иначе часть головки зуба рейки будет контактировать с заготовкой (нарезать её) не по эвольвенте.

Так как , а , то и при стандартных значениях ; .

Для исключения подреза при Zmin необходимо сместить инструмент от центра заготовки (положительная коррекция) так, чтобы , т. е.

или с учётом того, что , получим при коэффициент коррекции . Эта величина χ определяет нижний предел коэффициента коррекции.

Если увеличивать коэффициент χ, то толщина зуба Sa у вершины (рис. 79) будет уменьшаться и при некотором χmax наступит заострение зуба (Sa=0). Опасность заострения наиболее велика у колёс с малым числом зубьев (Z<15). Для предотвращения разрушения заострённого зуба коэффициент смещения χ назначают с расчётом, чтобы Sa≥0,2m.