Составление спецификации модели временного ряда.

Временной ряд – последовательность значений датированных переменных в различные дискретные моменты времени.

Модели временного ряда предназначены для объяснения уровня ряда изменением фактора t

t = 0, 1, 2, … , n

Переменная служит количественной характеристикой некоторого экономического объекта, поэтому изменение этой переменной во времени определяется факторами (движущими силами), показывающими различное воздействие на данный объект с течением времени.

Влияющие факторы можно разделить на три вида:

1) факторы, результирующее влияние которых на данный объект на протяжении длительного времени (по отношению к горизонту прогнозирования) не изменяет своего направления – «вековые» воздействия

Эти факторы, если они существуют, порождают монотонную составляющую тенденцию или тренд в структуре .

2) факторы, результирующее влияние которых на объект совершает законченный цикл в течение некоторого промежутка .

Эти факторы, если они существуют, порождают периодическую составляющую в структуре переменной - «циклические» воздействия

*Если , то циклическая составляющая называется сезонной. В общем случае

3) Факторы, результирующее влияние которых на объект нерегулярно изменяет интенсивность направления переменной (случайно, стахостически)

Обозначим некоторую периодическую функцию, заданную периодом :

Слагаемое с номером i в правой части называется i-той гармоникой.

Количество слагаемых n в правой части (2.8) может быть любым в зависимости от сложности изменений во времени данной периодической функции.

Рассмотрим периодическую функцию с целочисленным периодом :

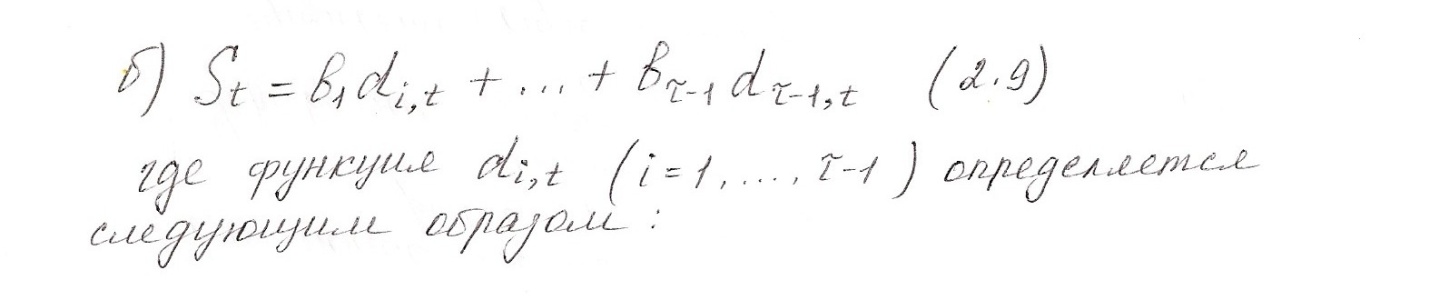
Символом обозначим некоторую хаотично изменяющуюся вокруг нулевого уровня функцию элемента (аргумента) t

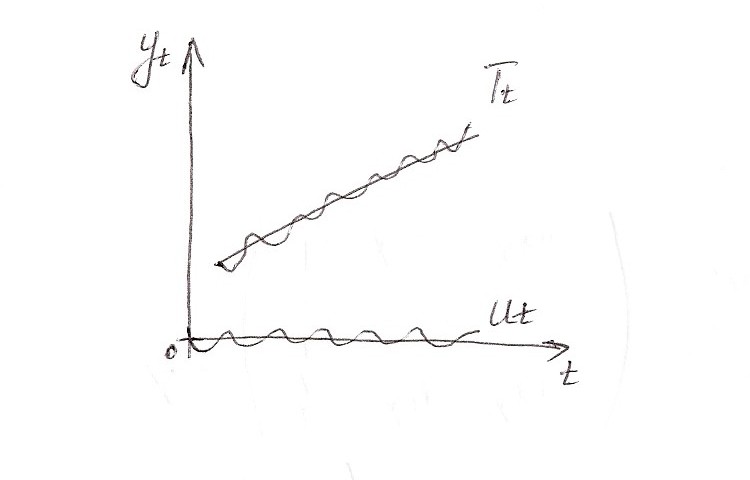
В итоге комбинации упомянутых выше функций

а) аддитивная

Она используется, когда амплитуда А циклической составляющей не зависит от времени

б) мультипликативная

Она используется, когда амплитуда А циклической составляющей изменяется со временем.

Билет №32

Оценка параметров множественной регрессионной модели методом наименьших квадратов.

Рассмотрим механизм применения МНК на примере идентификации модели в виде линейного уравнения множественной регрессии. + +

Для оценки параметров уравнения множественной регрессии обычно применяется метод наименьших квадратов (МНК), согласно которому следует выбирать такие значения параметров а, при которых сумма квадратов отклонений фактических значений результативного признака yi от теоретических значений ŷ минимальна, т. е. Q = -> min (77.1)

То есть Q= = ->min

Для нахождения параметров функции, соответствующих ее минимуму, необходимо вычислить производную этой функции по параметрам и решить полученные уравнения относительно параметров.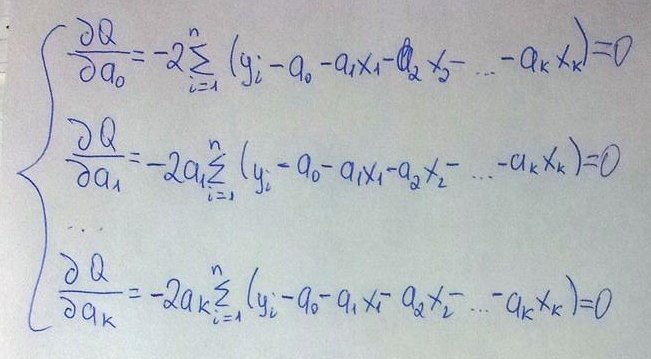 (77.2)

Отсюда после некоторых преобразований получается система нормальных уравнений метода наименьших квадратов.

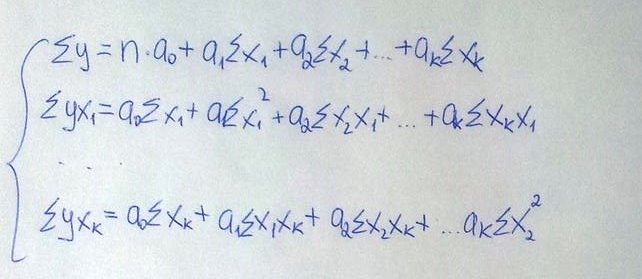(77.3)

Убедимся, что решение системы уравнений соответствует минимуму функции. Для этого необходимо, чтобы вторые частные производные были положительными.

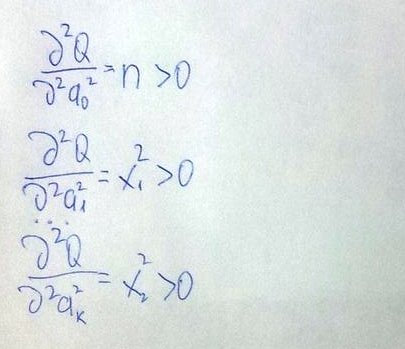
Следовательно, решение системы (77.3) соответствует минимуму функции (77.1)

Билет №33