27) Рівняння Шредінгера
Оснновне рівняння квантової механіки було сформульоване Шредінгером в 1926р. Це рівняення, як і всі основні рівняння фізики, не виводяться, їх правильність підтверджується експериментально.
Рівняння Шредінгера має такий вигляд:
(1)
де
;
– хвильова функція координат і часу;
– маса частинки;
– оператор Лапласа (
);
–
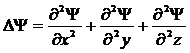потенціальна
енергія частинки в силовому полі, в
якому рухається частинка .
– уявна одиниця.
Рівняння
(1) є рівнянням другого порядку з
частинними похідними. Воно справедливе
для будь-якої частинки, яка рухаїться
з малою швидкістю(
).
Рівняння
(1) також називають рівнянням Шредінгера,
що залежить від часу, оскільки воно
містить похідну від функції
по часу.
Поряд
з часовим рівнянням Шредінгера, існує
стаціонарне рівняння Шредінгера, в
якому виключено залежність Ψ від часу.
Воно має сенс для тих задач, в яких
потенціальна енергія
U
не залежить від часу
Стаціонарне рівняння Шредінгера має вигляд:
де
Ψ(
)
– хвильова функція координат;
Е – повна енергія частинки.
Функції Ψ, які задовольняють рівняння Шредінгера при повному значенні Е, називають власними функціями. Ті значення Е, для яких рівняння мають розв’язок, називають власними значеннями.
Отже,
рівняння Шредінгера дає змогу знайти
не тільки конкретний вигляд функції
в заданому зовнішньому полі
, а й визначити її зміну з часом
.
28) Властивості хвильової функції. Квантування енергії.
29) Хвильова функція та її статичний зміст.
30) Частинка в одномірній прямокутній «потенціальній ямі».
Частинка в прямокутній потенціальній ямі
У випадку одномірної потенціальної ями потенціальна енергія частинки U(x) набуватиме такі значення (для простоти приймаємо, що частинка рухається вздовж осі ОХ) (рис. 176):
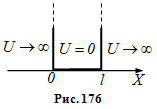
де
–
ширина “ями”, а енергія відраховується
від дна ями.
Рівняння
Шредінгера у випадку одномірної ями
запишемо у вигляді
.
За
умовою задачі (нескінченно високі
"стінки") частинка не проникає за
границі "ями", тому імовірність
її виявлення за границями "ями"
дорівнює нулю. На границях "ями"
(при x = 0
і x = l)
неперервна хвильова функція повинна
перетворюватися в нуль. Отже, граничні
умови мають вигляд
.
В
границях "ями" (
)
рівняння Шредінгера має вигляд
,
,
де
.
Загальний розв’язок цього диференціального рівняння:
.
Оскільки
,
то
.
Отже,
.
Умова
виконується
лише при
,
де n
– цілі числа, тобто необхідно, щоб
.
Тоді
i
.
Рівняння
Шредінгера задовольняється лише при
значеннях
,
що залежать від цілого числа n.
Отже,
енергія
частинки
в потенціальній "ямі" з нескінченно
високими стінками не може бути довільною,
а набуває лише певних дискретних
значень, тобто квантується. Квантові
значення енергії
називають
рівнями енергії, а число n,
яке визначає енергетичні рівні частинки,
називають квантовим числом.
Знайдемо власні хвильові функції
.
Сталу
інтегрування A визначаємо з умови
нормування
.
Звідси
.
Тоді власна хвильова функція має вигляд:
,.
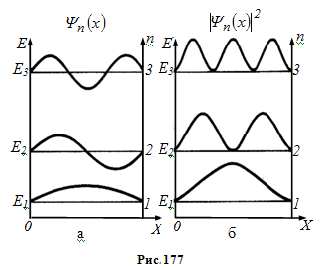
На
рис. 177, а
наведені графіки функції
при
,
рис. 177, б
– густини ймовірності знаходження
частинки на різних відстанях від
“стінок” ями для
.
Наприклад, у квантовому стані з n = 2 частинка не може знаходитись посередині "ями" і в той же час однаково часто може перебувати в її лівій або правій частині.