1.Електричний струм називається упорядкований рух електричних зарядів. Упорядкований рух носіїв заряду в провідному середовищі називається струмом провідності. Основним способом збудження струму є створення і підтримання в провідниках електор. Поля.

Якщо за однакові проміжки часу Δt крізь поперечний переріз провідника проходять однакові заряди Δq і напрям струму не змінюється , то такий струм називається стаціонарним або постійним.

Сила постійного струму: I=Δq/Δt

Силою струму називають скалярну величину, яка чисельно дорівнює зарядові, що переміщується крізь поперечний переріз за проміжок часу.

Густина струму чисельно дорівнює відношенню сили струму , що проходить крізь перпендикуляр до напрямку руху носіїв поверхню ds, до площини цієї поверхні.

J=dI/dS.

2. Виділимо у провіднику довільний об’єм V , обмежений замкненою поверхнею S. Нехай в об’ємі V міститься заряд q, розподілений з об’ємною p=p(x,y,z,t).

Якщо з об’єму V крізь поверхню S витікає позитивний заряд dq протягом часу dt , то за одиницю часу витікає заряд , що дорівнює силі струму.

-dq/dt=∫j_пdS

Заряд q виразимо через об’ємну густину

q=∫divjdV

Після цього отримаємо

∫dp/dt - інтегральна форма закону

dp/dt= -divj – диференціальна

Ці рівняння виражають закон збереження заряду в електродинаміці : зміна заряду dp/dt у об’ємі V обмеженому поверхнею S відбивається в наслідок витікання або втікання його крізь цю поверхню.

Це означає, що постійний струм немає витоків і станів зарядів , тобто в середині замкненої поверхні S у будь якій точці електричні заряди не виникають і не зникають : на місце зарядів які вибули за одиницю часу, надходять нові – густина струму j у даній точці залишається постійним.

3. Сила струму в однорідному провіднику прямо пропорційна напрузі на кінцях цього провідника

I=U/R

Закон Ома для неоднорідного поля : I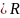 ₁₂ = + ε₀

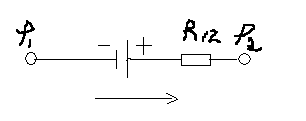
Спад напруги на ділянці кола визначаться , як алгебраїчна різниці потенціалів на її кінцях і електрорушійної сили, що діє на цій ділянці.

Якщо з’єднати кінці 1 і 2 неоднорідної ділянки , то їх потенціали вирівняються .

І утворить замкнене коло . Тоді користуючись законом Ома

I=ε/R+T ,

де R- опір провідника приєднаного до полюсів джерела струму.

4. Закон Джоуля Ленса :

Кількість теплоти , що виділяється струмом в провіднику пропорційна силі струму , часу його проходження і падіння напруги.

Кількість теплоти постійного струму

Q=I²Rt

t-час,

R-опір провідника.

Якщо струм змінюється з часом то за час dt теплота:

dq=i²Rdt,

за час t кількість теплоти в провіднику

Оскільки повна к-ть теплоти виділеної за час t дорівнює роботі, виконаний струмом за цей час , то

Q=∫dQ= – інтегральна форма закону Джоуля Ленса

Формули виражають сумарну к-ть теплоти ,що виділяється в провіднику к-ть теплоти що виділене в окремих місцях провідника можна визн. через диференціальний закон.

За законом Джоуля Ленса в цьому об’емі протягом часу dt виділиться к-ть теплоти

dQ=I²dRdt=j²pdVdt

dV=dSdI- елементарний об’єм

Кількість теплоти, яка виділяється в одиниці об`єму провідника за одиницю часу наз. Питомою потужністю струму:

W=dQ/dVdt

Маємо ω=ρj²

Користуючись зак. Ома одерж.:

ω=jE

ω=σE²

σ-характер матеріалу провідника

Е- центр поля інертного струму

5. Перше правило Кіргофа: виражає закон збереження в будь-якій точці кола постійного струму і стосується вузлів розгалуженого кола: алгебраїчна сума сил струмів, які сходяться у вузлі дор. 0\

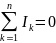
Струми, які приходять до вузла записуємо зі знаком «+», які виходять – -

Наприклад для потока 1 правило Кірхгофа записуєть

I₁-I₂-I₃-I₄+I₅=0

2 правило Кірхгофа: У контурі алгебраїчна сума спадів напруг дор. алгебр. сумі електрорушійних сил, які діють у цьому контурі

За законом Ома запишемо

I₁R₁= +ε₁

I₂R₂= +ε₂

I₃R₃= +ε₃

Додавши ці рівняння отримаємо

I₁R₁+I₂R₂+I₃R₃=ε₁+ε₂+ε₃

6.Роботою виходу електрону з металу називається найменшою енергією, яку треба затратити для виходу електрона з металу у вакуум А= .

Явище виходу електронів з металів називається емісією . Емісія електронів може відбуватися при бомбардуванні поверхні металу електронами або іонами(вторинна) під дією світла (фотоелектронна)

Емісію зумовлену тепловим рухом електронів, називають термоелектронною.

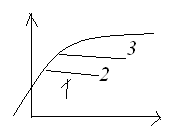
Явище термоелектронної емісії за допомогою вакуумної лампи з 2ма електронами , яку називають вакуумним діодом , якщо збільшувати напругу катодом і анодом при сталій температурі , то сила термоелектронного струму буде більшою проте залежність I маэ нелінійний характер тобто закон Ома не використовується. При наступному збільшення Н, І досягає макс. значення яке називається струмом насичення. При струмі насичення всі електрони , які вилітають з катода достають анода.

7) Магнітне поле постійних струмів у вакуумі. Магнітна взаємодія струмів.

Як зазначалось, магнітне поле, що створюється рухомими елек­тричними зарядами (або струмами), є векторним.

Стаціонарні магнітні поля створюються постійними струмами, сила яких I повністю визначена, якщо задано густину струму.Силовою характеристикою магнітного поля у вакуумі є його індукція , яка визначає величину і напрям сили, що діє на провідник з струмом у магнітному полі. На елемент довжини 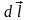провідника зі струмом I у зовнішньому магнітному полі з індукцією діє сила Ампера

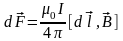
Магнітна взаємодія струмів.Ампер встановив закон :

сила дії 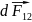першого елемента струму на другий прямо пропорційна добуткові елементів струмів, обернено пропорційна квадратові відстані між ними і залежить від взаємної орієнтації цих елементів:

10) Застосування теореми про циркуляцію в для підрахунку магнітної індукції поля соленоїда і тороїдаю

Для соленоїда:

По теоремі циркуляції Bl=

BL-циркуляція

nlI-струм охоплюючий контур

nl-число витків

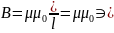
Для тороїда:

R – радиус тора;r–радиус контура;

N– число витков.

Якщо контур всередині тороїда:

він охоплює струм NI,то:

Контур за тороїдом: магнітного кола немає.

8) Закон Біо-Савара-Лапласа. Поля прямого і кругового струмів.

=

є математичним записом закону Біо—Савара—Лап- ласа.Цей закон є узагальненням експериментальних даних, от­риманих Біо і Саваром у 1820 р. У скалярній формі закон Біо — Савара — Лапласа записують так:

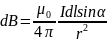
Закон Біо — Савара—Лапласа є одним із основних експеримен­тальних законів електромагнітних явищ і він, подібно до закону Кулона, лежить в основі класичної електродинаміки. Цей закон дає змогу розрахувати індукцію магнітних полів струмів.

За прин­ципом суперпозиції у провідниках із струмом скінченної довжини результуючу індукцію в довільній точці магнітного поля визнача­ють як векторну суму елементарних значень індукції, створюваних окремими елементами провідника

Для прямого струму:

Для кругового струму:

9) Циркуляція вектора магнітної індукції. Теорема про циркуляцію в.

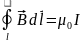називають законом повного струму, або теоремою про циркуляцію вектора індукції магнітного поля.

Закон повного струму справедливий для довільних струмів і формулюється так: циркуляція вектора індукції магнітного поля постійних струмів по довільному замкненому контуру дорівнює ал­гебраїчній сумі струмів, які охоплюються цим контуром.

є диференціальною формою закону повного струму, або основним диференціальним рівнянням стаціонарного магнітного поля.

11. Дія магнітного поля на струми і заряди. Закон Ампера. Сила Лоренца.

Дія магнітного поля на рухомі заряди визначається силою Лоренца. Сила, що діє на провідник зі струмом у магнітному полі називається силою Ампера. Сили взаємодії провідників зі струмом визначаються законом Ампера. Коли в магнітне поле внести провідник зі струмом, то на нього діє сила (сила Ампера). Візьмемо дві рейки M₁N₁ і M₂N₂ і помістимо на них тонкий металевий стержень QР. До рейок приєднаємо джерело з електрорушійною силою ε.

Нехай лінії індукції магнітного поля B напрямлені зверху вниз. Якщо замкнути електричне коло, то виникає сила Ампера F, напрямлена вправо, яка зміщує стержень вздовж рейок. Зі зміною напрямку струму змінюється і напрям сили Ампера.

Французький вчений Андре Марі Ампер в 1820 р. експериментально встановив, що сила F, яка діє на прямолінійний провідник із струмом в однорідному магнітному полі, прямо пропорційна добутку сили струму І на довжину провідника l на магнітну індукцію B і синус кута між напрямом струму I і вектором B,

де У випадку неоднорідного поля сила dF, що діє на елемент провідника довжиною dl, по якому протікає струм І, визначається за формулою

Напрям сили F визначається правилом лівої руки. Якщо долоню лівої руки розмістити так, щоб лінії індукції B входили в долоню, а витягнені пальці показували напрям струму І, то відхилений великий палець покаже напрям сили Ампера F.

На елемент струму Idl у магнітному полі з індукцією B діє сила Ампера величиною , де - кут між векторами і . Якщо q – заряд частинки, n₀ – кількість частинок в одиниці об’єму, то , де v - середня швидкість упорядкованого руху частинок; j –густина струму; s – площа поперечного перерізу провідника. Тоді

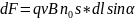
В об’ємі міститься кількість частинок . Якщо q>0, тоді кут α між векторами і . буде також кутом між векторами і . Тому формулу (5.10) можна переписати у вигляді .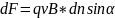

Сила, що діє на одну заряджену частинку (сила Лоренца), буде:

У векторній формі для зарядів q>0 дістанемо і

. Сила Лоренца перпендикулярна до площини, в якій лежать вектори v і B. Напрям сили Лоренца треба визначати за правилом векторного добутку (рис.5.7 ).

Оскіль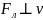ки , то сила Лоренца не виконує роботи, а тільки змінює напрям руху частинок і за характером їхнього відхилення можна визначити знак і величину питомого заряду частинки .