Задание 10.

Исследование 27 семей по среднедушевому доходу (Х) и сбережениям (Y) дало результаты: = (100 – 2 * k) = 88 у.е., S_x = (40 - k) = 34 у.е.,

= (30 + k) = 36 у.е., S_y = (20 + k) = 26 у.е., = (3700 + k) = 3706 (у.е.)². При α = 0,05 проверить наличие линейной связи между Х и Y.

Решение:

Линейный коэффициент корреляции

Зависимость между признаками Х и У – прямая и по шкале Чеддока сильная.

Для оценки статистической значимости коэффициента корреляции рассчитывают двухсторонний t-критерий Стьюдента:

,

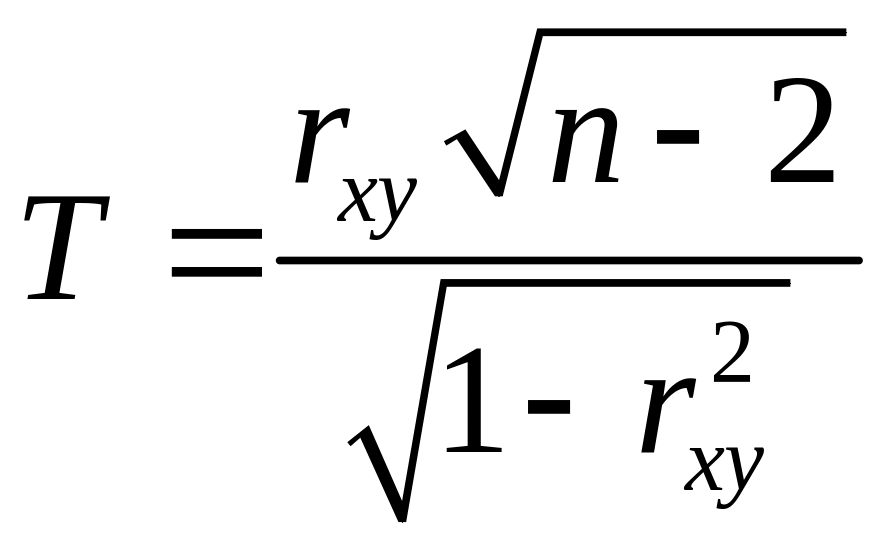который имеет распределение Стьюдента с k = n – 2 и уровнем значимости α.

В нашем случае

и .

Поскольку , то коэффициент корреляции существенно отличается от нуля. При α = 0,05 наличие линейной связи между Х и Y значимо.

Расчеты проводить с точностью до трех знаков после запятой.

1. Вероятность того, что в страховую компанию (СК) в течение года обратится с иском о возмещении ущерба первый клиент, равна (15+k)/100. Для второго клиента вероятность такого обращения равна (20+ k)/100. Для третьего клиента - (10+k)/100. Найдите вероятность того, что в течение года в СК обратится хотя бы один клиент, если обращения клиентов - события независимые.

Решение:

Обозначим события: А_i – в страховую компанию обратится i-ый клиент (i=1,2,3). Пусть событие F – обращение хотя бы одного клиента в компанию в течение года. Противоположное событию F событие = =

P(F)= 1-P( ) = 1 – P ( ) = 1 - P( ) P( ) P ( ) = 1- 0,79*0,74*0,84 = 1-0,491064 = 0,508936 0,51

Ответ: 0,51

2. В магазин поступают телевизоры с трех заводов: (30+k)% с первого завода, (25+k)% - со второго, остальные с третьего. При этом первый завод выпускает (20+ k)% телевизоров со скрытым дефектом, второй, соответственно, (10+ k)%, а третий - (15+ k)%. Какова вероятность приобрести исправный телевизор в этом магазине? Если в телевизоре обнаружен дефект, то на каком заводе, скорее всего, изготовлен этот телевизор?

Решение:

Обозначим события: А_i – телевизор поступил в магазин от i-ого завода (i=1,2,3). Пусть событие F – телевизор поступил в исправном состоянии.

По условию:

P( )= = 0,36

P( )= = 0,31

P ( )==0,33

= 0,74

= 0,84

= 0,79

По формуле полной вероятности:

P(F)= 0,36*0,74+0,31*0,84+0,33*0,79=0,7875

Событие –телевизор поступил со скрытым дефектом.

P( ) = 1-P(F)= 1-0,7875=0,2125 0,213

По условию:

= 0,26

= 0,16

= 0,21

Находим по формуле Байеса:

( )= = 0,27

( )= =0,232

( )==0,325

Таким образом, даже после наступления события имеет самый высокий уровень вероятности по сравнению с А₁ и А₂. Поэтому можно предположить, что телевизор с дефектом поступил, скорее всего, из третьего завода.

Ответ: Вероятность приобретения исправного телевизора: 0,787

В третьем.

3. При данном технологическом процессе (75+k)% всей продукции - 1-го сорта. Найдите наивероятнейшее число первосортных изделий из (200+10k) изделий и вероятность этого события.

Решение:

Пусть событие А – продукция является изделием первого сорта.

По условиям Р(А)= 0,81

np-q m₀ np+p ,

где q=1-p

p=0,81

q=0,19

n=260

210,6-0,19 m₀ 210,6+0,19

210,41 m₀ 210,72

Единственное целое число, которому может быть равно m₀ в данном неравенстве m₀=210

Применяем локальную формулу Муавра-Лапласа, так как

npq = 260*0,81*0,19=40,01420

x==0,09

По табличным данным f(0,09)=0,3973

P_16,2100,063

Ответ: 210; 0,063

4. Для подготовки к экзамену студенту нужна определенная книга, которая может находиться в каждой из 4-х доступных студенту библиотек с вероятностью (0,3+k/100). Составить закон распределения числа посещаемых библиотек. Обход прекращается после получения нужной книги или посещения всех четырех библиотек. Найдите математическое ожидание и дисперсию этой случайной величины (СВ).

Решение:

Случайная величина Х – число библиотек, которые доступны студенту – может принимать значения 1,2,3,4.

Обозначим события: А_i –нужная книга находится в i-ой библиотеке (i=1,2,3,4). Тогда вероятность того, что книга будет обнаружена в первой библиотеке Р (Х=1)=Р (А₁)=0,36

Студент посетит вторую библиотеку лишь при условии, что необходимой книги в первой библиотеке не окажется. P(Х=2)= P ( A₂) = P ( Р(A₂)= (1-0,36)*0,36=0,2304

Аналогично:

P(Х=3)= P ( A₃) = P ( Р(A₃)= 0,64²*0,36=0,147456

P(Х=4)= P ( ) = P ( Р( )=0,64³=0,262

Ряд распределения случайной величины Х имеет вид:

xi	1	2	3	4
Pi	0,36	0,2304	0,147456	0,262

Проверяем, что

Найдем математическое ожидание:

а = М(Х)= =

Найдем дисперсию:

D(X)= M(X²) – a²

M(X²)=

Теперь D(X)=6,732-2,288²=1,497

Ответ: М(Х)=1

D(X)= 1,497

5. В нормально распределенной совокупности 16% значений X меньше 12 и 46% значений X больше 18. Найдите параметры этой совокупности.