21

Оглавление

Теория вероятностей и математическая статистика

Задание 1. 2

Задание 2. 6

Задание 3. 7

₇

Ответ:11,6 7

Задание 4. 8

Задание 5. 10

Задание 6. 11

Задание 7. 12

Задание 8. 13

Задание 9. 15

Задание 10. 17

Литература 21

k = 6

Задание 1.

Распределение случайной величины Х - заработной платы сотрудников на фирме (в у.е.) - задано в виде интервального ряда:

Таблица 1.1

Хmin i (аi)	300	310+10*k	320+20*k	330+30*k	340+40*k	350+50*k
Хmax i (bi)	310+10*k	320+20*k	330+30*k	340+40*k	350+50*k	360+60*k
Частота mi	10	20	30	25	10	5

Найти: , S_х. Построить теоретическое нормальное распределение и сравнить его с эмпирическим с помощью критерия согласия Пирсона χ² при α = 0,05.

Решение:

Таблица 1.2

Хmin i (аi)	300	340	380	420	460	500
Хmax i (bi)	370	440	510	580	650	720
Частота mi	10	20	30	25	10	5

Для расчета статистических характеристик от интервального ряда перейдем к дискретному, приняв за варианты середины интервалов.

Таблица 1.3

Хi	335	405	475	545	615	685
Частота mi	10	20	30	25	10	5

Найдем: , S_х.

Среднее арифметическое взвешенное:

Дисперсия:

Среднее квадратическое отклонение:

_{Таблица 1.4}

xi	ni	xini	xi2ni
335	10	3350	1122250
405	20	8100	3280500
475	30	14250	6768750
545	25	13625	7425625
650	10	6150	3782250
720	5	3425	2346125
Сумма	100	48900	24725500

Построим теоретическое нормальное распределение и сравним его с эмпирическим с помощью критерия согласия Пирсона χ² при α = 0,05.

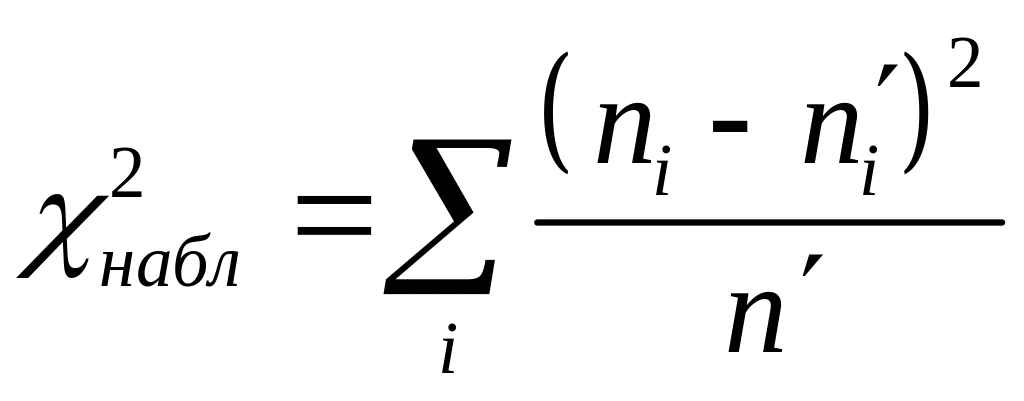
По таблице критических точек распределения , по уровню значимости  = 0,05 и числу степеней свободы k = n – 3 = 9 – 3 = 6 находим критическую точку правосторонней критической области

Так как ,то гипотезу о нормальном распределении генеральной совокупности принимаем. Другими словами эмпирические и теоретические частоты различаются незначимо (уровень значимости  = 0,05).

Таблица 1.5

xi	ni	ui	φ(ui)	ni'	ni - ni'	(ni - ni')2	(ni - ni')2/ni'
320	10	-1,71	0,0925
360	20	-0,93	0,2589
400	30	-0,16	0,3939
440	25	0,62	0,3292
480	10	1,40	0,1497
520	5	2,17	0,0379
Сумма	100