18

МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное агентство морского и речного транспорта

ФИЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО

УЧРЕЖДЕНИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МОРСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ

ИМЕНИ АДМИРАЛА Ф.Ф. УШАКОВА»

в г. РОСТОВЕ-на-ДОНУ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по курсу МАТЕМАТИЧЕСКИЕ ОСНОВЫ

СУДОВОЖДЕНИЯ

на тему ОЦЕНКА ТОЧНОСТИ

МЕСТА СУДНА ПРИ ОБСЕРВАЦИИ ПО ДВУМ ЛИНИЯМ ПОЛОЖЕНИЯ

Ростов-на-Дону

2005

Вычисление модулей и направлений градиентов.

Градиентом называется вектор, выражающий скорость изменения навигационного параметра по нормали к изолинии (к линии положения). Градиент направлен в сторону возрастания навигационного параметра. Абсолютные величины и направления градиентов навигационных параметров необходимо знать для решения двух основных задач судовождения:

- для определения координат места судна обобщенным методом линий положения (аналитическое и графо-аналитическое решение);

- для оценки точности обсервованного места судна методом эллипса погрешностей и методом средней квадратической погрешности (СКП) обсервованной точки.

В первой задаче модуль и угол , выражающий направление градиента относительно истинного меридиана, входят в качестве коэффициентов при неизвестных в уравнение линии положения:

.

Градиент можно также представить в проекциях на оси прямоугольной системы координат, совмещенных с меридианом и параллелью счислимой точки:

В этом случае уравнение линии положения принимает вид:

При оценке точности обсервованного места судна модули градиентов входят в формулы элементов эллипса погрешностей и СКП места судна.

Общая формула модуля градиента в практических задачах записывается так:

(1)

Здесь - приращение навигационного параметра в направлении от счислимой точки к определяющей;

- расстояние по нормали между этими точками, называемое переносом.

Из формулы (1) следует:

т.е. модуль градиента можно рассматривать как коэффициент пропорциональности между приращением навигационного параметра и величиной переноса . Так как в большинстве случаев измеряемое для обсерваций навигационные параметры выражаются в градусной мере или же в морских единицах длины , а перенос выражается в милях или кабельтовых, то размерность модуля градиента должна соответствовать размерности навигационного параметра, отнесенной к морским единицам длины.

Направления градиентов относительно истинного меридиана определяются углом в круговом счете.

От величины градиентов и от их направлений в значительной степени зависит точность определения координат судна.

Формулы эллипса погрешностей и СКП обсервованной точки показывают, что предпочтительнее измерять те навигационные параметры, градиенты которых имеют наибольшую величину. Например, если в пределах видимости имеется несколько визуальных ориентиров, то для определения места судна пеленговать следует ближайшие из них, так как градиенты пеленгов обратно пропорциональны расстояниям от судна до ориентира. А чем больше модули градиентов, тем меньше погрешность обсервованной точки.

Из этих же формул следует, что лучшая точность обсервации достигается, когда угол между линиями положения, который либо равен углу между градиентами, либо является дополнением его до , будет близок к прямому. При определении места судна по расстояниям и по высотам светил модули градиентов равны единице и угол между градиентами становится основным фактором, влияющим на точность обсервации.

Выбирая ориентиры и способы обсервации, необходимо также принимать во внимание условия видимости, состояние штурманских приборов и ряд других обстоятельств, от которых зависит точность измерения навигационных параметров и качество обсервации.

Пример.

Находясь по счислению на расстоянии от маяка, взяли его пеленг . Вычислить модуль и направление градиента пеленга.

Решение. Модуль градиента пеленга вычисляем по формуле , приняв в ней расстояние , снятое с карты:

Направление градиента:

При вычислении угла вместо счислимого значения пеленга взяли пеленг, полученный измерением.

Итак, по направлению - вдоль переноса – пеленг ориентира изменяется (увеличивается) на на одну милю.

Пример.

Секстаном измерили горизонтальный угол между ориентирами и . Исправив поправками отсчет, взятый по шкале прибора, получили .

С карты сняли расстояния из счислимой точки до ориентиров, а также расстояние (базу) между ними:

Вычислить модуль градиента горизонтального угла.

Решение. По формуле:

получили: или

Градиент направлен к центру окружности, проходящей через оба ориентира и вершину угла (место судна).

Оценка точности места судна методом эллипса погрешностей.

Расчетные формулы элементов эллипса погрешностей.

Влияние на обсервованное место судна случайных погрешностей измерений навигационных параметров наиболее полно и строго оценивается методом эллипса погрешностей.

Эллипс погрешностей обладает следующими свойствами:

- он является единственной фигурой, во всех точках которой плотность вероятности постоянна;

- вероятность нахождения действительного места судна в пределах эллипса погрешностей больше, чем в любой другой фигуре, ограничивающей область такой же площади;

- оси эллипса погрешностей показывают направление действия наибольшей и наименьшей погрешности обсервации.

Расчет вероятности нахождения места судна в области, ограниченной эллипсом, производится по формуле:

(2).

При эллипс называют средним квадратическим или средним, или стандартным. Вероятность нахождения места судна в границах среднего эллипса по формуле (2) составляет

Если увеличить полуоси среднего эллипса в 1,1774 раз, то получим эллипс погрешностей, называемый вероятным. Для такого эллипса

При получим При Эллипс погрешностей, которому соответствует такая вероятность, называют предельным. Его полуоси в три раза больше полуосей среднего эллипса.

Элементами эллипса погрешностей называют его большую , малую полуоси и угол , служащий для ориентировки эллипса относительно линий положения. При определении места судна по двум линиям положения элементы среднего эллипса погрешностей вычисляют по формулам:

(3)

(4)

где - средние квадратические погрешности измерений навигационных параметров;

- модули градиентов навигационных параметров;

- острый угол между первой и второй линиями положения.

Угол всегда откладывается внутри острого угла между линиями положения, т.е. . Угол указывает направление большой полуоси эллипса относительно той линии положения, которая соответствует навигационному параметру, измеренному с погрешностью .

Известно, что

(5)

Величину называют смещением линии положения.

Формулы элементов эллипса погрешностей через смещения линий положения имеют вид:

(6)

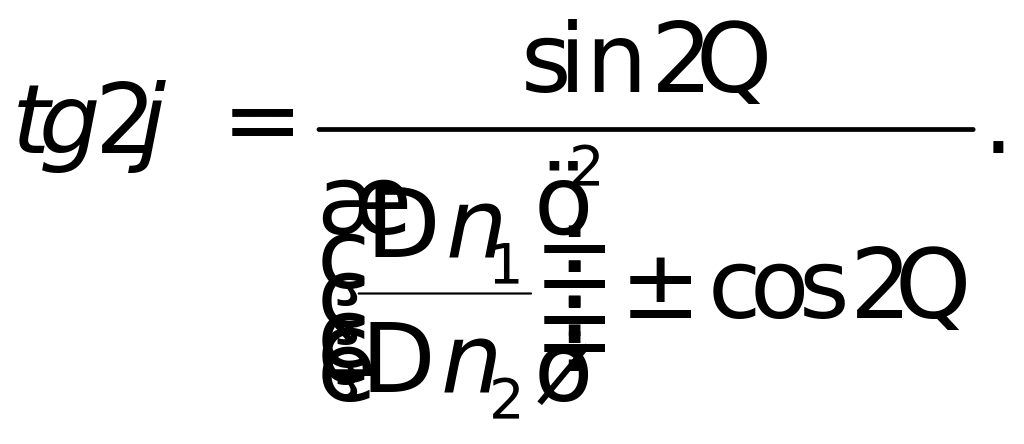(7)

Большая полуось эллипса погрешностей составляет меньший угол с более точной линией положения, т.е. с той линией положения у которой величина смещения меньше.

Когда обе линии положения равноточны , то большая полуось эллипса направлена по биссектрисе острого угла . Точность, с которой следует вычислять элементы эллипса погрешностей по формулам , зависит от вида обсерваций и применяемых ТСС, от условий плавания и, конечно, от того, какая информация о местоположении судна требуется для обеспечения безопасности плавания. Например, на подходе к берегу элементы эллипса целесообразно рассчитывать в милях с указанием десятых долей. В стесненных водах, где условия плавания значительно сложнее и, как правило, обеспечена более высокая точность обсерваций, полуоси эллипса следует вычислять до десятых долей кабельтова. Наконец, в узкостях, в зоне действия РНС ближнего действия и при хороших по точности обсервациях по НИСЗ может возникнуть надобность рассчитать элементы эллипса с точностью до десятых метров и даже до метров.

В открытом море производить оценку точности обсерваций для целей судовождения не требуется. Однако иногда такие задачи приходится решать при исследованиях радионавигационных и спутниковых систем, в частности, новых судовых приемоиндикаторов и новых методов измерений навигационных параметров.

Таким образом, расчет элементов эллипса надо производить с такой точностью, которая соответствует точности обсервации и с учетом требований безопасности плавания.

Пример.

Место судна определено по двум визуальным пеленгам, Рассчитать элементы эллипса погрешностей и построить его главные оси по этим элементам, если с карты сняли мили; с карты сняли мили;

Решение.

1. Составим формулы градиентов:

2. Вычисляем угол между линиями положения:

3. Составляем формулы для расчета элементов эллипса:

=

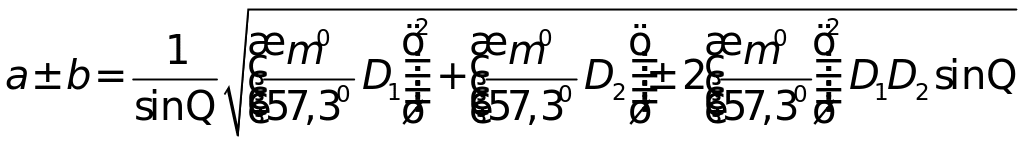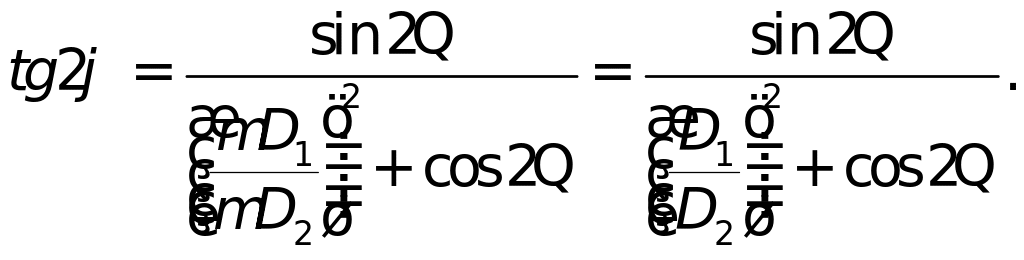
4. Подставляя числовые значения, произведем расчеты:

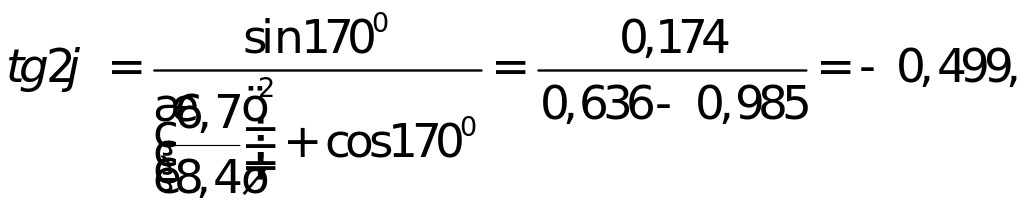
так как имеет знак минус, угол находится во второй четверти:

и

5. По вычисленным элементам и построили на карте предельный эллипс ошибок:

.

Для этого в обсервованной точке , внутри острого угла , между линиями положения проводим под углом ко второй линии положения. На этой прямой в обе стороны от точки откладываем отрезки, равные . Затем от точки перпендикулярно большой оси эллипса строим малые полуоси , как показано на рисунке (1)

Рис. 1