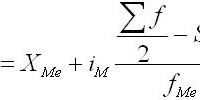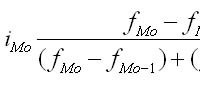13. Относительные показатели вариации:
коэффициент осцилляции
коэффициент вариации
относительное линейное отклонение
1. Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг общей средней.
2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений (модуль отклонений) от средней величины.
3. Коэффициент вариации - отношение среднего квадратического отклонения к средней арифметической, применяется для сравнения вариаций различных признаков, используется как характеристика однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%.
14. Ряды распределения по качественному признаку.
Статистические ряды распределения представляют собой упорядоченное распределение единиц совокупности по группам и группировкам. Ряды распределения изучают структуру совокупности, позволяют изучить ее однородность, размах и границы. Ряды распределения, образованные по качественным признакам, называют атрибутивными. Атрибутивные ряды образуются по качественным признакам, которыми могут выступать занимаемая должность работников торговли, профессия, пол, образование и т.д. Вариационные ряды – ряды распределения единиц совокупности по признакам, имеющим количественное выражение, т. е. образованы численными значениями.
ПРИМЕР: Распределение работников предприятия по образованию.
Образование работников |
Количество работников |
|
|
абсолютное |
в % к итогу |
высшее |
20 |
15,4 |
неполное высшее |
25 |
19,2 |
среднее специальное |
35 |
26,9 |
среднее |
50 |
38,5 |
ИТОГО |
130 |
100 |
В данном примере группировочным признаком выступает образование работников предприятия (высшее, среднее). Данные ряды распределения являются атрибутивными, поскольку варьирующий признак представлен не количественными, а качественными показателями. Наибольшее число составляют работники со средним образованием (порядка 40%); остальные работники распределяются на группы по данному качественному признаку: со средним специальным образованием - 25%; с неполным высшим - 20%; с высшим - 15%.
15. Понятие структурных средних.
Для характеристики рядов распределения (структуры вариационных рядов), наряду со средней, используются структурные средние: мода и медиана, квартиль и дециль. Мода и медиана наиболее часто используются в экономической практике.
Мода - варианта, которая наиболее часто встречается в ряду распределения (в данной совокупности).
В дискретных вариационных рядах мода определяется по наибольшей частоте. При характеристике социальных групп населения по уровню дохода следует использовать модальное значение, нежели среднее. Средняя будет занижать одни показатели и завышать другие — тем самым уравнивания доходы всех слоев населения.
В интервальных вариационных рядах моду определяют приближенно по формуле:
ХМ0 — нижняя граница модального интервала;
hMo - величина (шаг, ширина) модального интервала;
f1 - локальная частота интервала, предшествующего модальному;
f2 - локальная частота модального интервала;
f3 - локальная частота интервала, следующего за модальным.
Медиана - это численное значение признака у той единицы совокупности, которая находится в середине ранжированного ряда (построенного в порядке возрастания, либо убывания значений изучаемого признака). Медиану иногда называют серединной вариантой, т.к. она делит совокупность на две равные части таким образом, чтобы по обе ее стороны находилось одинаковое число единиц совокупности.
Нахождение медианы в интервальных вариационных рядах требует предварительного определения интервала, в котором находится медиана, т.е. медианного интервала – этот интервал характеризуется тем, что его кумулятивная (накопленная) частота равна полусумме или превышает полусумму всех частот ряда.
XMe -нижняя граница медианного интервала
hMe -величина медианного интервала;
SMe-1-сумма накопленных частот интервала, предшествующего медианному интервалу;
fMe -локальная частота медианного интервала.
Квартиль –это четвертая часть совокупности, определяется как и медиана, только сумму частот необходимо разделить на 4, а при определении квартильного интервала, кумулятивная частота должна быть больше или равна четверти суммы частот совокупности.
Дециль – делит совокупность на десять равных частей. Определяется аналогично как и квартиль, только сумму частот необходимо разделить на 10.
16. Виды: Мода и медиана Медиана — это такое значение признака, которое разделяет ранжированный ряд распределения на две равные части — со значениями признака меньше медианы и со значениями признака больше медианы. Для нахождения медианы, нужно отыскать значение признака, которое находится на середине упорядоченного ряда. где Хm — нижняя граница медианного интервала; im — медианный интервал; Sme— сумма наблюдений, которая была накоплена до начала медианного интервала; fme — число наблюдений в медианном интервале. Свойства медианы Медиана не зависит от тех значений признака, которые расположены по обе стороны от нее. Аналитические операции с медианой весьма ограничены, поэтому при объединении двух распределений с известными медианами невозможно заранее предсказать величину медианы нового распределения. Медиана обладает свойством минимальности. Его суть заключается в том, что сумма абсолютных отклонений значений х, от медианы представляет собой минимальную величину по сравнению с отклонением X от любой другой величины Графическое определение медианы Для определения медианы графическим методом используют накопленные частоты, по которым строится кумулятивная кривая. Вершины ординат, соответствующих накопленным частотам, соединяют отрезками прямой. Разделив поп олам последнюю ординату, которая соответствует общей сумме частот и проведя к ней перпендикуляр пересечения с кумулятивной кривой, находят ординату искомого значения медианы. Определение моды в статистике Мода — значение признака, имеющее наибольшую частоту в статистическом ряду распределения. Определение моды производится разными способами, и это зависит от того, представлен ли варьирующий признак в виде дискретного или интервального ряда. Нахождение моды и медианы в контрольных по статистике происходит путем обычного просматривания столбца частот. В этом столбце находят наибольшее число, характеризующее наибольшую частоту. Ей соответствует определенное значение признака, которое и является модой. В интервальном вариационном ряду модой приблизительно считают центральный вариант интервала с наибольшей частотой. В таком ряду распределения мода вычисляется по формуле: где ХМо — нижняя граница модального интервала; imo — модальный интервал; fм0, fм0-1,, fм0+1 - частоты в модальном, предыдущем и следующем за модальным интервалах. Модальный интервал определяется по наибольшей частоте. Мода широко используется в статистической практике при анализе покупательного спроса, регистрации цен и т. д. Соотношения между средней арифметической, медианой и модой Для одномодального симметричного ряда распределения средняя арифметическая, медиана и мода совпадают. Для асимметричных распределений они не совпадают.
Просмотреть все изображения
