
- •Означення матриць, типи матриць.
- •2. Розкриття невизначеностей з використанням правила Лопіталя.
- •3.Неперервність ф-ї в точці та на проміжку.
- •Означення неперервності в точці
- •Основні властивості неперервних функцій
- •4.Означення похідної.
- •Похідні основних елементарних функцій
- •6.Диференціал ф-ї. Геометричний зміст. Застосуваннядо наближених обчислень.
- •7.Основні теореми диференціального числення.
- •8. Означення ф-й багатьох змінних.
- •9.Частинні похідні фбз.
- •10.Похідна за напрямом. Градієнт фбз.
- •11.Екстремуми фбз.Необхідна і достатня умови існування екстремуму ф-ї 2-х змінних.
- •12. Первісна.Невизначений інтеграл.
- •13.Визначений інтеграл.
- •14.Поняття та різновиди невласних інтегралів.
- •15.Звичайні диференціальні р-ння(др).Основні поняття.Задача Коші.
- •21.Числові ряди.
- •22.Ряд геометричної прогресії.Гармонічний ряд.
- •23. Достатня ознака збіжності для знакододатних рядів.
- •24.Знакозмінні ряди.Абсолютна та умовна збіжність.
- •25.Степеневі ряди.Інтервал та радіус збіжності.
- •26.Означення ф-ії багатьох змінних
- •1.Означення матриць, типи матриць.
- •2. Розкриття невизначеностей з використанням правила Лопіталя.
Похідні основних елементарних функцій
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Правила диференціювання
|
|
|
|
Похідна складеної функції Похідна оберненої функції
![]()
![]()
Похідна
функції,
заданої параметрично: ![]()
Таблиця інтегралів
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.Диференціал ф-ї. Геометричний зміст. Застосуваннядо наближених обчислень.
Якщо
функція ![]() має
похідну
має
похідну ![]() в
точці
в
точці ![]() ,
то вираз
,
то вираз ![]() називається диференціалом (differential)
функції в цій точці і позначається
символом
називається диференціалом (differential)
функції в цій точці і позначається
символом ![]() .
Тобто,
.
Тобто,
![]() .
.
Зауваження. Диференціал функції в даній точці є головною лінійною частиною приросту функції, пропорційною приросту аргументу з коефіцієнтом пропорційності :
![]() .
.
Диференціал незалежної змінної ототожнюється з її приростом, тобто
![]() .
.
Для будь-якої диференційовної в точці х функції формулу можна записати так:
![]() .
.
Звідки отримаємо, що
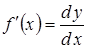 ,
,
тобто похідну можна розглядати як відношення двох диференціалів.
Геометричний зміст диференціала
Нехай
, ![]() та
існує
та
існує ![]() .
За означенням диференціала
.
За означенням диференціала ![]() .
.
Р
|
Скористаємося
геометричним змістом похідної:
Зтрикутника
Отже,
диференціал функції
в
точці
визначає
приріст ординати дотичної до кривої
в точці
|
Застосування диференціала в наближених обчисленнях
З
означення похідної функції в
точці
випливає,
що її приріст ![]() можна
подати у вигляді:
можна
подати у вигляді: ![]() ,
де
,
де ![]() ,
якщо
,
якщо ![]() .
.
Отже,
при малих ![]() має
місце наближена рівність:
має
місце наближена рівність:
![]() ,
тобто
,
тобто ![]() .
.
Звідки
![]() .
(3.12)
.
(3.12)
Формула
(3.12) дозволяє знаходити значення
функції
в
точці ![]() ,
якщо відомі значення
,
якщо відомі значення ![]() і
,
з точністю
і
,
з точністю ![]()
![]() ,
,
де ![]() .
.
Приклад
3.13. Наближено
обчислити значення ![]() .
.
Розв’язання. В
даному випадку ![]() ,
, ![]() .
Покладемо
.
Покладемо ![]() ,
що відповідає
,
що відповідає ![]() в
градусній мірі;
в
градусній мірі;
![]() .
.
За формулою (3.12), отримаємо:
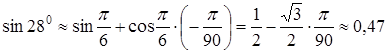 ,
,
тобто ![]() .
.
Для
того, щоб оцінити абсолютну і відносну
похибки, скористаємось більш точним
значенням, отриманим за допомогою
калькулятора: ![]() .
Тоді
.
Тоді ![]() ,
а відносна похибка
,
а відносна похибка ![]() дорівнюватиме:
дорівнюватиме:
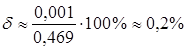 .
.
7.Основні теореми диференціального числення.
Правила Лопіталя розкриття невизначеностей
Теорема 3.10. (І правило Лопіталя). Якщо:
1)
функції ![]() і
і ![]() диференційовні
на інтервалі
диференційовні
на інтервалі ![]() ,
, ![]() для
всіх
для
всіх ![]() ;
;
2) ![]() ;
;
3)
існує скінченна або нескінченна
границя 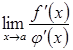 ,
,
то
існує границя 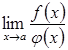 ,
причому має місце рівність:
,
причому має місце рівність:
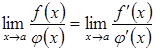 .
.
Приклад
3.24. Обчислити
границю 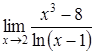 .
.
Розв’язання. Ми
маємо невизначеність типу ![]() .
Функції
.
Функції ![]() і
і ![]() задовольняють
умови теореми в деякому околі точки
задовольняють
умови теореми в деякому околі точки ![]() .
Застосуємо правило Лопіталя:
.
Застосуємо правило Лопіталя:
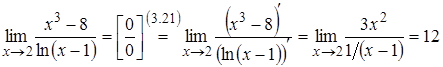 .
.
Теорема Коші (Cauchy theorem) (про відношення приростів двох функцій)
Теорема 3.9. Якщо функції і
1)
неперервні на відрізку ![]() ,
,
2) диференційовні в інтервалі , причому ,
то
в цьому інтервалі існує точка ![]() ,
, ![]() така,
що має місце рівність:
така,
що має місце рівність:
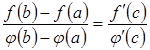 .
.
Теорема Ферма
Теорема
3.6. Нехай
функція
визначена
на інтервалі
і
в деякій точці ![]() має
найбільше або найменше значення. Тоді
якщо в точці
існує
похідна, то вона дорівнює нулю, тобто
має
найбільше або найменше значення. Тоді
якщо в точці
існує
похідна, то вона дорівнює нулю, тобто ![]() .
.

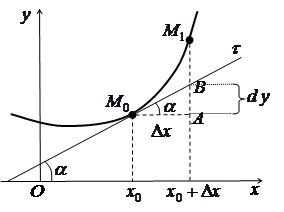 ис.
3.4
ис.
3.4