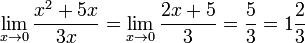1. Означення матриць, типи матриць.

Означення: Матрицею називається прямокутна таблиця чисел, яка має m рядків і n стовпчиків. Їх позначають великими літерами A,B,C і т.д.

Типи матриць:

1. Квадратна матриця, в якої елементи головної діагоналі дорівнюють одиниці, а всі інші нулю називається одиничною матрицею.

2. Якщо всі елементи матриці, що знаходяться по один бік від головної діагоналі, дорівнюють нулю, то матриця назівається трикутною.

3. Нульовою матрицею наз матриця, у якоъ всі елементи – нулі і познач літерою О.

4. Одиничною наз квадратна матриця,у якої елементи, які стоять на гол діагоналі=1, інші елементи =0, познач Е.

5. Діагональною наз матриця у якої ел-ти які стоять на гол діагоналі – довільні, а всі інші – 0.

Дії над матрицями.

*,-, А*1/2/3.., А*В. при А*1.. усі її ел-ти * на це число.

При + +ся відповідно елементи матриці( Аа пов бути однакового розміру) А*А Е тільки тоді, коли №рядків=стовпців. Добутком А розмірності х на В є така С, кожний елемент якої = сумі добутків елементів ітого рядка А. Вл добутків матриць:

1. А*в не=в*а / 2) (а*в)с=а*(вс) / 3) а*(в+с)=ас+вс / 4) (а+в)*с=ас+вс / 5) а0=0а=0 / 6) а*Е=Е*а=а

Суми матриць і добутку матриць виконуються рівності:

A+B=B+A; 2. aA=Aa 3. a(A+B)=aA+aB 4. (a+b)A=aA+bA 5. a(bA)=(ab)A

Оберненна матриця.

Матриця називається об до А якщо виконується співвідношення: .

Оберенні матриці існують для невироджених, квадратних не особливих матриць.

Знаходять обернену матрицю таким чином:

1. _{обчислити визначник А і впевнитись в її невиродженості(визначник не=0)}

2. замінити кожний елемент матриці її алгебраїчним доповненням

3. транспонувати одержану матрицю

4. 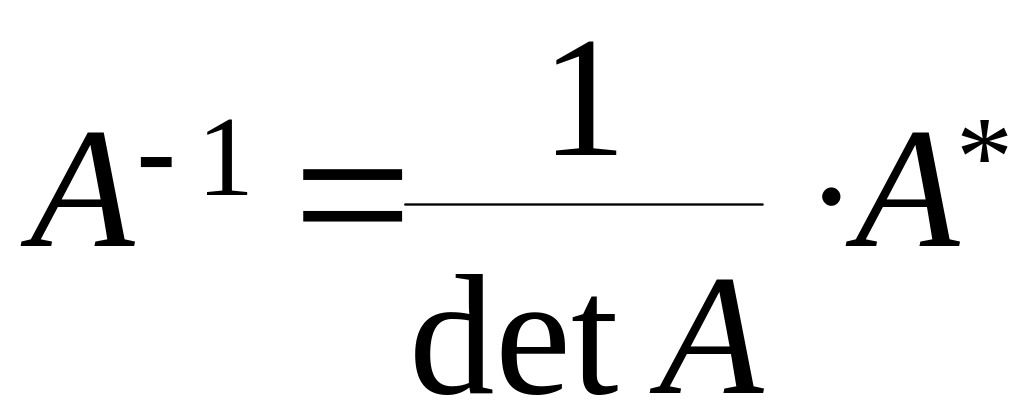_{поділити всі її елементи на знач визначника.}

2. Розкриття невизначеностей з використанням правила Лопіталя.

Правило Лопіталя.

Нехай виконані умови:

функції f(х) та g(х) визначені і диференційовані в колі точки х0;

частка цих функцій  в точці х0 має невизначеність вигляду  або ;

існує .

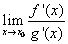Тоді існує 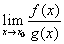 і виконує рівність:

    

• 

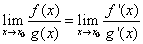
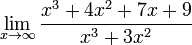• тут можна застосувати правило Лопіталя 3 рази а можна вчинити інакше. Можна розділити і чисельник, і знаменник на x найбільшою мірою(у нашому випадку 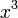 ). В даному прикладі виходить:

• ;

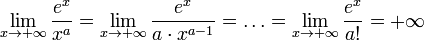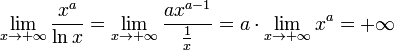•  при  .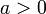

  Лопіталь де Гійом Франсуа (1661-2.02.1704 рр.). Французький математик, Видав перший друкований підручник по диференціальному обчисленню – “Аналіз нескінченно малих” (1696р.). В підручнику є правило Лопіталя – правило знаходження межі дробу, чисельник і знаменник якого прямує до 0. Крім того, він створив курс аналітичної геометрії конічних перетинів. Йому також належить дослідження і розвиток за допомогою математичного аналізу декількох важких задач по геометрії і механіці, а також одне із рівнянь знаменитої задачі о браністохроні.  1.   Правило Лопіталя.  Нехай виконані умови:  1.  функції f(х) та g(х) визначені і диференційовані в колі точки х₀;  2.  частка цих функцій   в точці х₀ має невизначеність вигляду   або  ;  3.  існує  .  Тоді існує   і виконує рівність:              (1)  а) Наслідок.  Нехай:  1. Визначені в колі точки х₀ функції f(х),  g(х) та їх похідні до n-го порядку включно;  2. Частки  ,  , …,   мають невизначеність вигляду   або  ;  3. Існує  , тоді                 (2)  б) Приклад 1.  Знайти:  .  Розв’язання:  Функції   та   визначені з усіма своїми похідними в околі точки х=0.  Маємо:  .