15. Уравнение среднего времени оценки пористости горных пород

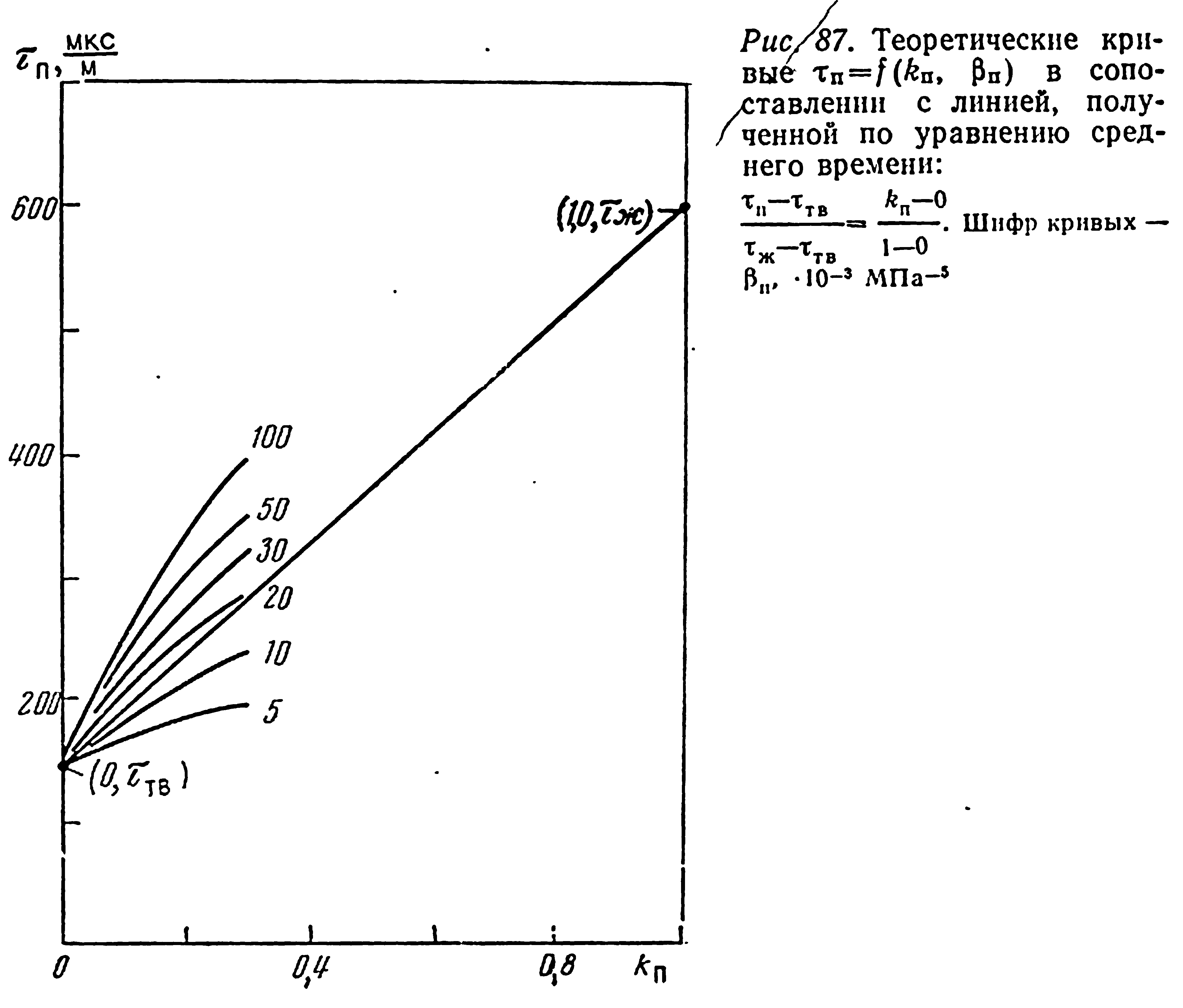
Как видно из рис. 87, кривые интервального времени пробега продольных волн (тп=1/Vр) с указанными выше параметрами можно лишь очень приближенно апроксимировать прямыми линиями, проходящими через две точки с координатами (0, ттв) и (1, тж)> где ттв и тж — интервальное время в твердой фазе и в жидкой фазе. Уравнение этих прямых имеет вид

Это уравнение называют уравнением среднего времени (М. Р. Вилли, А. Р. Грегори и А. В. Гарднер, 1956 г.). Его чаще записывают в виде

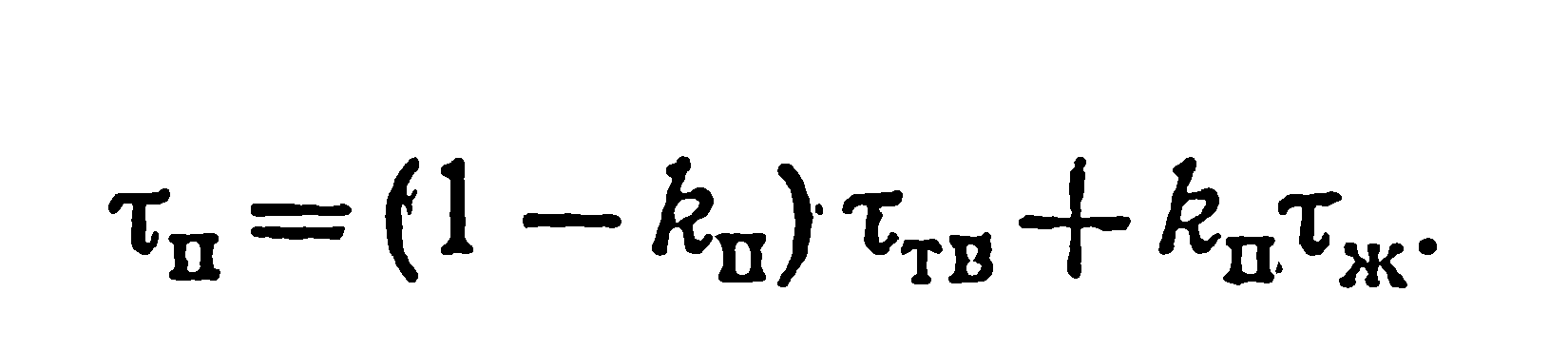
Таким образом, линейное уравнение A2.51) является весьма приближенным. Однако, как показывает опыт, оно довольно хорошо описывает экспериментальные данные, полученные в пластовых условиях (р—рпл=40-^-50 МПа) на чистых сцементированных породах с первичной пористостью. Для его использования нужно знать значения ттв и тж.

Интервальное время пробега продольных волн в твердой фазе породы Ттв, мкс/м:

Интервальное время пробега продольных волн в жидкости зависит от вида жидкости (нефть, вода): для нефти — от газонасыщенности последней, давления и температуры; для воды — от минерализации, давления и температуры [1, 3].

В глинистых породах с межзерновой пористостью коэффициент сжимаемости пор возрастает, и уравнение среднего времени перестает удовлетворять прямой линии. Известны два эмпирических способа, как преодолеть это несоответствие.

Первый способ заключается в усложнении слоистой модели породы путем добавления третьего глинистого слоя. Это уравнение, предложенное В. Н. Дахновым:

где тп и тгп — показатели степени, зависящие соответственно от структуры и степени цементации коллектора и изменяющиеся с уплотнением породы от 0,7 до 1,5.

Описанные выше теоретические уравнения и эмпирические зависимости среднего времени от коэффициента пористости можно использовать лишь при приведении скорости или интервального времени пробега упругих волн к условиям естественного залегания пород, т. е. к эффективному напряжению (р—рПл) и пластовой температуре Т. Для этого может быть использовано выражение [7, 15]:

16. Поглощение упругих волн в горных породах, коэффициенты поглощения и их зависимость от физических свойств пород.

В сплошных твердых, жидких и газообразных средах энергия волн упругости расходуется на трение между колеблющимися частицами, превращаясь в тепловую, и рассеивается в пространстве.

В скважинных исследованиях применяются зонды, размер которых позволяет приближенно считать фронт волны у приемника плоским (я=0). Уравнение A2.66) в этом случае принимает вид:

где S — база прибора — расстояние между двумя источниками упругих волн.

Откуда получим коэффициент поглощения

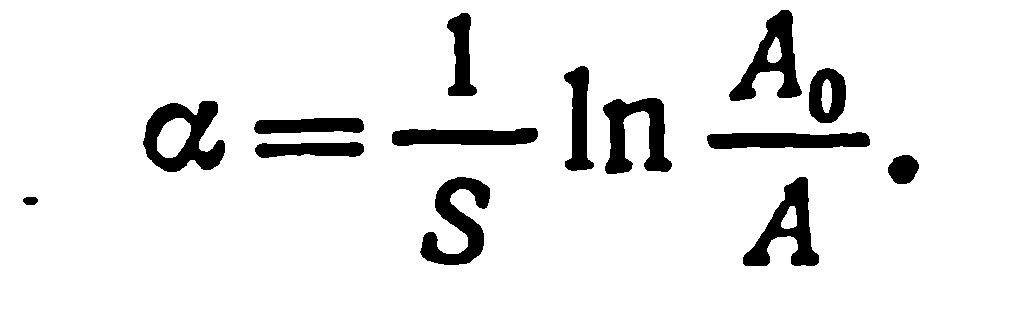
Уравнение A2.68) позволяет учесть рассеяние упругих волн в пространстве. Его величина в реальных жидкостях и газах может быть оценена с помощью коэффициента классического кирхгоффо-стоксова поглощения Кс> обусловленного потерями, связанными с вязкостью и теплопроводностью среды (Л. Д. Ландау, Е. М. Лившиц, 1965 г.):

Распространение продольных и поперечных волн в реальных горных породах сопровождается поглощением энергии, что связано с проявлением вязкости (неидеальной упругости среды) и неидеального теплообмена. Так же, как и в жидкостях, поглощение здесь также обусловлено кирхгоффо-стоксовым механизмом, учитывающим вязкость и теплопроводность среды, который проявляется на расстояниях, соизмеримых с длиной волны:

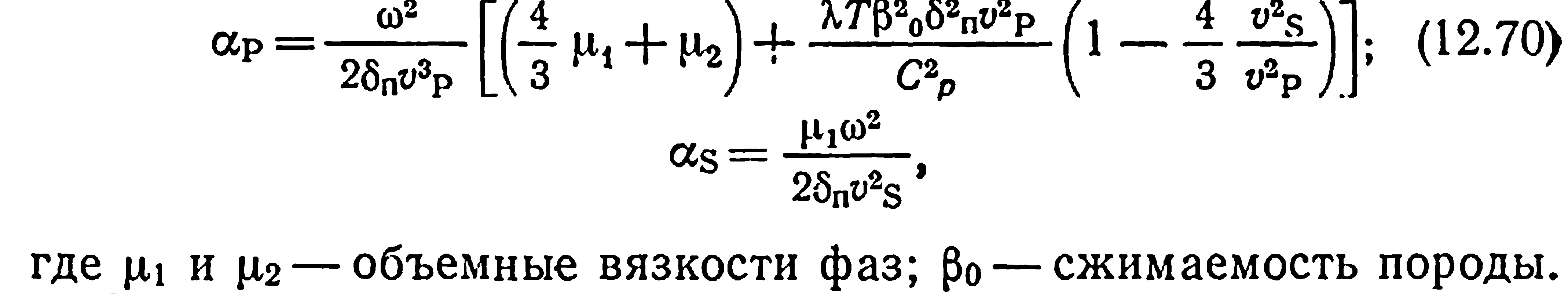
Как видно из уравнений, поглощение продольных волн связано с тепловыми и вязкоинерционными процессами, а поглощение поперечных волн — только с вязко-инерционными процессами.

Экспериментальными исследованиями процесса поглощения упругих волн установлен ряд весьма важных зависимостей, которые не противоречат приведенным выше уравнениям. Например, коэффициенты поглощения ар и as увеличиваются с частотой звука (рис. 89, а, б). Расчеты показывают, что. сочетание термического и вязкоинерционного затухания приводит к тому, что коэффициенты

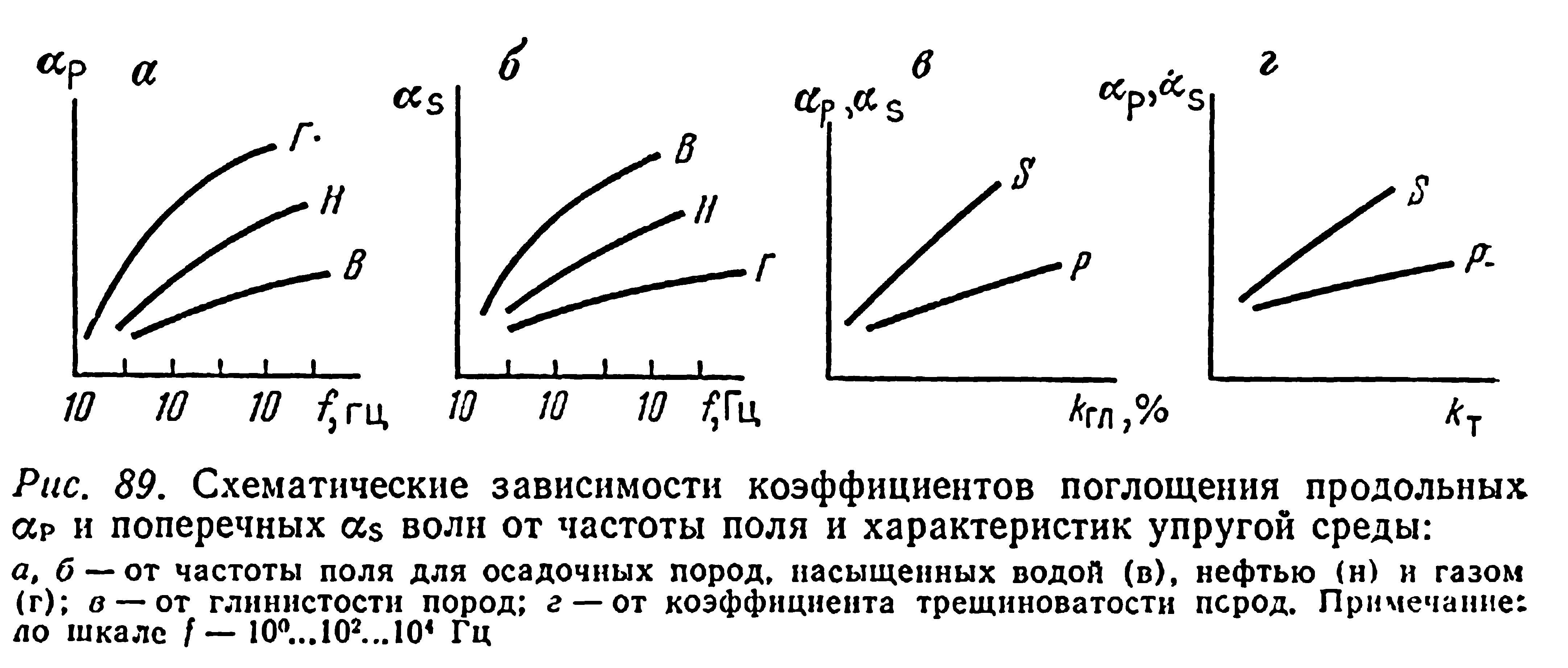
Эти обстоятельства могут оказаться весьма перспективными при исследовании скважин, бурящихся на нефильтрующихся промывочных жидкостях.

Коэффициенты поглощения возрастают с увеличением глинистости гранулярных пород (см. рис. 89, в) и коэффициентов трещиноватости трещиновато-кавернозных пород (см. рис.89,г). Поперечные волны более чувствительны к увеличению «неоднородности» порового пространства. Более глубокое использование теоретических формул A2.70)

затруднено в связи с трудностями экспериментальной оценки объемных вязкостен твердых тел. Поэтому часто для расчетов коэффициентов поглощения волн упругости в твердых телах пользуются эмпирическими формулами (Л. Д. Ландау, Е. М. Лившиц, 1965 г.): где n>1.

Кроме того, ввиду разнообразия возможных механизмов поглощения волн упругости в многофазных средах для оценки реальных величин коэффициентов поглощения волн Р и S предлагается использовать суммарный коэффициент поглощения (Б. Н. Ивакин, Е. В. Карус, О. Л. Кузнецов)

где Терм — коэффициент термического поглощения звука; Ви —коэффициент вязко-инерционного поглощения и Кс — коэффициент Кирхгоффо-Стоксова поглощения.

Расчеты показывают, что коэффициент классического поглощения акс может быть в осадочных породах существенно меньше, чем добавочные механизмы поглощения Так, для частоты f=10 кГц в газонасыщенном пласте Вероятно, такой подход позволит приближенно рассчитать основные параметры упругого поля для ряда моделей пористой среды. Однако эта проблема в приложении к реальным многофазным породам еще весьма далека от разрешения [18].