32. Электромагнитные колебания. Затухающие колебания. Вынужденные колебания - переменный ток.

Можно показать, что уравнение свободных колебаний для заряда q = q(t) конденсатора в контуре имеет вид

(1) где q" - вторая производная заряда по времени. Величина является циклической частотой. Такими же уравнениями описываются колебания тока, напряжения и других электрических и магнитных величин.

Одним из решений уравнения (1) является гармоническая функция . Период колебаний в контуре дается формулой (Томсона): . Величина  , стоящая под знаком синуса или косинуса, является фазой колебания.

Фаза определяет состояние колеблющейся системы в любой момент времени t. Ток в цепи равен производной заряда по времени, его можно выразить

Затухающие колебания — колебания, энергия которых уменьшается с течением времени.

Вынужденные колебания - колебания, происходящие под воздействием внешних периодических сил

18. Закон Био-Савара-Лапласа, его применение к расчету полей.

18. Закон Ампера. Взаимодействие параллельных токов.

Ампер открыл, что сила dF, с которой магнитное поле действует на элемент проводника dlс током, который находится в магнитном поле, равна  где dl - вектор, по модулю равный dl и совпадающий по направлению с током, В - вектор магнитной индукции.  Направление вектора dF может быть определено, используя (1), по правилу векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, которая действует на ток.  Модуль силы Ампера (см. (1)) равен  (2),где α — угол между векторами dl и В. 

18. Сила Лоренца. Определение радиуса траектории периода обращения, шага винтовой траектории при движении частиц в однородном магнитном поле.

Движение заряженной частицы в однородном постоянном магнитном поле.

В данном случае   и сила Лоренца имеет только магнитную составляющую  . Уравнением движения частицы, записанном в декартовой системе координат, в этом случае является:

Р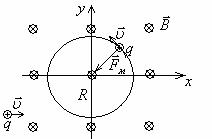 ассмотрим сначала случай, когда частица влетает под прямым углом к силовым линиям магнитного поля. В системе координат, показанной на рис. ,  , , и уравнение движения принимает вид:

, откуда следует, что вектор полного ускорения частицы  лежит в плоскости, перпендикулярной вектору  . Легко убедиться также в том, что вектор ускорения  перпендикулярен вектору скорости частицы  и составляет вместе с вектором  правую тройку векторов (как и должно быть по свойствам силы Лоренца). Действительно,

, Таким образом, ускорение частицы в каждый момент времени t направлено к центру кривизны траектории и играет роль нормального (центростремительного) ускорения. Модуль ускорения равен:

.

Траекторией движения является окружность , радиус R которой находим из условия:  , то есть  , откуда

Период обращения частицы

Отметим, что период обращения и соответственно угловая скорость движения частицы   не зависят от линейной скорости  .