8. Условия преломления напряжённости и индукции электрического поля на границе раздела диэлектриков.

Нормальная составляющая вектора D в непосредственной близости D_1n =D_2n . Циркуляция есть , где -тангенциальная составляющая . Т.к. циркуляция должна была быть равна нулю, то . При переходе от Е к D имеем . При переходе через границу раздела нормальная составляющая и тангенциальная составляющая при переходе изменяются скачком (терпят разрыв), а тангенциальная составляющая и нормальная составляющая изменяются непрерывно. , в среде с большей диэлектрической проницаемостью линии смещения гуще (т.е. D больше), чем в среде с меньшей

8. Электроемкость. Емкость уединенного проводника.

Будем рассматривать уединенный проводник, т. е. проводник, значительно удаленный от других проводников, тел и зарядов. Его потенциал, как известно, прямо пропорционален заряду проводника. Из опыта известно, что разные проводники, будучи при этом одинаково заряженными, имеют различные потенциалы. Поэтому для уединенного проводника можно записать  Величину  называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника задается зарядом, сообщение которого проводнику изменяет его потенциал на единицу. 

8. Конденсаторы. Расчет емкости плоского, сферического и цилиндрического конденсаторов.

Конденсатор - электрический прибор, состоящий из двух проводящих пластин, разделенных слоем диэлектрика. Конденсаторы служат для накопления зарядов с целью их отдачи в нужный момент времени, а также в цепях переменного тока для деления зарядов (параллельное соединение) и для деления напряжения (последовательное соединение). 

Плоский конденсатор. Две плоские параллельные пластины одинаковой площади S, расположенные на расстоянии d друг от друга, образуют плоский конденсатор. Если пространство между пластинами заполнено средой с относительной диэлектрической проницаемостью  , то при сообщении им заряда q напряженность электрического поля между пластинами равна  , разность потенциалов равна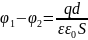  . Таким образом, емкость плоского конденсатора

Сферический конденсатор. Два проводника, имеющие форму концентрических сфер с радиусами R₁ и R₂ (R₂ > R₁), образуют сферический конденсатор. Используя теорему Гаусса, легко показать, что электрическое поле существует только в пространстве между сферами. Напряженность этого поля  где q - электрический заряд внутренней сферы;   - относительная диэлектрическая проницаемость среды, заполняющей пространство между обкладками; r - расстояние от центра сфер, причем  . Разность потенциалов между обкладками и емкость сферического конденсатора 

Цилиндрический конденсатор представляет собой два проводящих коаксиальных цилиндра радиусами R₁ и R₂ (R₂ > R₁). Пренебрегая краевыми эффектами на торцах цилиндров и считая, что пространство между обкладками заполнено диэлектрической средой с относительной проницаемостью  , напряженность поля внутри конденсатора можно найти по формуле:  , где q - заряд внутреннего цилиндра; h - высота цилиндров (обкладок); r - расстояние от оси цилиндров. Соответственно, разность потенциалов между обкладками цилиндрического конденсатора и его емкость есть   

 - энергия заряженного конденсатора

- формула Томсона для периода электромагнитных колебаний в колебательном контуре LC.