1. Закон Кулона. Принцип суперпозиции Закон сохранения заряда.

Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними , где k = 9*10⁹ м/Ф, а

Принцип суперпозиции: Напряжённость электрического поля системы зарядом равна векторной сумме направлений полей, которые бы создал каждый заряд по отдельности

Закон сохранения заряда утверждает, что во время взаимодействия некоторой замкнутой системы с окружающим пространством количество заряда которое выходит из системы через ее поверхность равно количеству заряда поступившего внутрь системы. Другими словами алгебраическая сумма всех зарядов системы равна нулю.

2. Теорема Гаусса электростатического поля в вакууме.

Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду  

3. Расчет полей с центральной, осевой и плоской симметрией.

а) На поверхности сферы начинаются их густота на r есть

,

4. Потенциал, разность потенциалов. Связь разности потенциалов и напряженности.

Потенциал электростатического поля — скалярная величина, равная отношению потен­циальной энергии заряда в поле к этому заряду

Разность потенциалов электрическая (для потенциального электрического поля то же, что напряжение электрическое) между двумя точками пространства (цепи); равна работе электрического поля по перемещению единичного положительного заряда из одной точки поля в другую.     

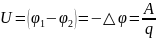
Установить связь меду напряженностью и разностью потенциалов для неоднородного поля можно, используя представление об эквипотенциальных поверхностях. Рассчитаем работу, совершаемую электрическим полем при перемещении электрического заряда с одной эквипотенциальной поверхности на соседнюю по направлению нормали к этой поверхности. Если расстояние между поверхностями по нормали  настолько мало, что на этом участке можно считать поле однородным, то можно записать выражение для элементарной работы через напряженность поля и расстояние между эквипотенциальными поверхностями:

С другой стороны, так как   , то работа поля по перемещению заряда из точки с потенциалом   в точку с потенциалом     равна:     Сравнивая полученные выражения для работы получим: В однородном поле   может быть любым. Если  , то: Из выражения следует, что в качестве единицы напряженности в системе единиц СИ можно использовать 

5. Проводники в электростатическом поле. Напряженность, потенциал и распределение зарядов в проводнике.

Если проводник поместить во внешнее электростатическое поле или зарядить его, то на заряды данного проводника будет действовать электростатическое поле, под действием которого они начнут двигаться. Движение зарядов (ток) будет длиться до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри данного проводника обращается в нуль. Это происходит в течение очень короткого времени. Действительно, если бы поле не было равно нулю, то в проводнике появилось бы упорядоченное движение зарядов без затраты энергии от внешнего источника, что не согласуется с законом сохранения энергии. Значит, напряженность поля во всех точках внутри проводника равна нулю: Если внутри проводника электрического поле отсутствует, то потенциал во всех точках внутри проводника одинаков ( ), т. е. поверхность проводника в электростатическом поле является эквипотенциальной. Это означает, что вектор напряженности поля на внешней поверхности проводника направлен по перпендикуляру к каждой точке его поверхности. Если это было бы не так, то под действием касательной составляющей Е заряды начали бы перемещаться по поверхности проводника, что, в свою очередь, противоречило бы равновесному распределению зарядов.