Лабораторная работа №2(ММ)

Частное учреждение образования «Техникум бизнеса и права»

Утверждаю

Зам. директора

по учебной работе

___________В.К.Голубков

«____»_____________2007

Специальность: 2-40 01 01 «Программное обеспечение информационных технологий»	Дисциплина: «Математическое моделирование»
Составлено в соответствии с рабочей учебной программы, утвержденной директором ТБП от

Лабораторная работа №2

Инструкционно –технологическая карта

ТЕМА: «»

ЦЕЛИ: 1. Развить способность работы в приложении MATHCAD.

2. Развитие логического мышления при вычислении значений простейших выражений, построении графиков функций.

ВРЕМЯ ВЫПОЛНЕНИЯ: 2ч

СОДЕРЖАНИЕ РАБОТЫ

1. Контрольные вопросы:

   1. Что называется

2. Теоретические сведения:

Операторы символьной математики

Приведем два примера на применение операторов символьной математики(в среде MATHCAD более 20 операторов):

Solve (решить) для решения уравнений и неравенств

Simplify(упростить) для преобразования алгебраических выражений

.

Заметим, что в решении неравенств квадратные скобки представляют объединение промежутков, а произведение неравенств – пересечение промежутков.

Операторы программирования

2. Порядок выполнения работы

1. Ответить на контрольные вопросы.

2. Проанализировать и выполнить в приложении MATHCAD следующие примеры

Пример 1

Дана система линейных алгебраических уравнений

.

.

Найти:

1. решение системы методом Гаусса (используя функцию rref());

2. определитель матрицы системы и определители , , ;

3. решение системы по формулам Крамера;

4. обратную матрицу А^-1 (проверить А^-1А=Е и АА^-1=Е);

5. решение системы по формуле Х=А^-1b «матричный метод»;

6. решение системы с помощью функции lsolve(A,b), которая возвращает вектор решения системы линейных уравнений;

7. решение системы с помощью блока решения given … find() – дано … найти.

Решение

1. Решение системы методом Гаусса – условно названное решение системы с применением функции rref(А_b)).

С помощью функции augment(A,b) образуется расширенная матрица системы линейных уравнений, далее функция rref(А_b) возвращает матрицу, эквивалентную исходной, где матрица системы оказывается приведенной к единичной матрице. Последний четвертый столбец матрицы A_reduced – решение системы линейных уравнений.

ORIGIN:=1

A_b:= augment(A,b) A_reduced:= rref(А_b)

A_reduced = x:= A_reduced x=

2. Вычисление определителей матрицы системы и определители , , :

А₁:=А А₂:=А А₃:=А

А₁ :=b А₂ :=b А₃ :=b

:=|A| :=|A₁| :=|A₂| :=|A₃|

3. Решение системы по формулам Крамера:

x=

4. Вычисление обратной матрицы А^-1:

А^-1·A= A ·А^-1 =

Представление элементов в виде дробей можно получить, выделив и установив числовой формат Format Result Fraction.

5) Решение системы по формуле Х=А^-1b «матричный метод»:

Х:=А^-1·b x=

6) Решение системы с помощью функции lsolve(A,b):

Х:=lsolve(A,b) x=

7) Решение системы с помощью блока решения given … find()

Вводится матрица системы линейных уравнений А, столбец свободных членов b и вектор-столбец из нулевых(можно задавать любые значения) стартовых значений искомого решения. Далее given система уравнений Ах=b найти х (find(х)) – для условия равенства в блоке следует нажимать Ctrl+=:

ORIGIN:=1

Given

А·х=b

x:= find(x) x=

Пример 2

Найти все решения системы линейных алгебраических уравнений

В этом примере система имеет не единственное решение и дается представление множества решений.

Решение

Функция rref(А_b), аргументом которой является расширенная матрица системы линейных уравнений, возвращает матрицу A_reduced ступенчатого вида, эквивалентную исходной, с двумя нулевыми строчками:

ORIGIN:=1

A_b:= augment(A,b)

A_reduced:= rref(А_b)

A_reduced =

Данная система уравнений оказалась эквивалентна системе из двух уравнений с четырьмя неизвестными

Неизвестные х₁ и х₃ являются главными(базисными) переменными, неизвестные х₂ и х₄ являются свободными.

Решение неоднородного уравнения равно сумме частного решения уравнения при нулевых значения свободных переменных (х₂ =0 и х₄ =0 ) и общего решения однородного уравнения. Общее решение однородного уравнения является линейной комбинацией фундаментальных решений – базиса решения. В данном примере имеем два фундаментальных решения: одно – частное решение однородного уравнения, когда х₂=1 и х₄=0; другое частное решение, когда х₂=0 и х₄=1:

Частное решение неоднородного уравнения (вектор х₀) при нулевых значениях свободных переменных. Стартовый вектор х – нулевой вектор.

Given

А·х=b

х₂=0

х₄ =0

х₀:=Find(x)

Частное решение однородного уравнения (вектор х₁)

Given

А·х=b

х₂=1

х₄ =0

х₁:=Find(x)

Частное решение однородного уравнения (вектор х₂)

Given

А·х=b

х₂=0

х₄ =1

х₁:=Find(x)

Таким образом, получили решение данной системы уравнений в виде:

x(t):=x₀+t₁·x₁+ t₂·x₂ , или

При любых значениях параметров t₁ и t₂ вектор x(t) удовлетворяет исходной системе уравнений; значения параметров выбраны с помощью функции rnd(x), генерирующей числа из промежутка (0,х):

Пример 3

Найти все решения системы линейных алгебраических уравнений

Решение

Функция rref(А_b), возвращает матрицу A_reduced, в одной строке которой элемент последнего столбца равен 1 с предшествующими нулевыми элементами. Этой строке соответствует противоречивое уравнение

0·x₁+ 0·x₂ + 0·x₃ + 0·x₄ =1

ORIGIN:=1

A_b:= augment(A,b)

A_reduced:= rref(А_b)

A_reduced =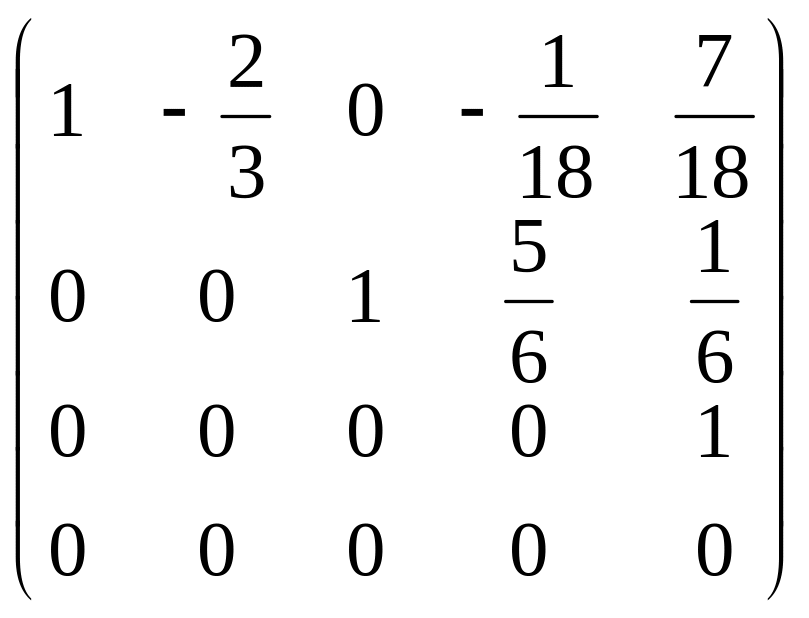

В этом случае система уравнений не имеет решения.