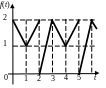Вариант: 10

Задание 1. Найти изображение следующих функций:

а) ; б) .

Задание 2. По данному графику оригинала найти:

а) изображение ступенчатой функции, используя теорему запаздывания;

б) изображение для периодической функции; в) изображение, используя преобразование Лапласа.

а) a4	б)
в)

.Задание 3. Восстановить оригинал по изображению : .

Задание 4. Найти оригинал, учитывая, что изображения представляются в виде суммы элементарных дробей: .

Задание 5. Средствами операционного исчисления найти частные решения дифференциальных уравнений при указанных начальных условиях: а) б)

Задание 6. Охотник, имеющий четыре патрона, стреляет по дичи до первого попадания или до израсходования всех патро­нов. Вероятность попадания при первом выстреле рав­на 0,6; при каждом последующем — уменьшается на 0,1. Найти закон распределения, функцию распределения и математическое ожидание числа патронов, израсходованных охотником.

Задание 7. Для данных выборок определить выборочное среднее , выборочную дисперсию , «исправленную» выборочную дисперсию , моду Mo, медиану Me, размах R. Для a) составить вариационный и статистический ряды; для б) найти эмпирическую функцию распределения; для в) построить гистограмму и полигон, эмпирическую функцию распределения .

а) 4, 4, 3, 8, 5, 3, 2, 2, 1, 1.

б)	xi	3	7	11	15	19	22	23
	ni	10	8	1	2	7	9	1

в)	xi	[0; 4)	[4; 8)	[8; 12)	[12; 16)	[16; 20)	[20; 24)
	ni	2	3	3	4	2	1

Задание 8. Для установления среднего размера вклада определенной категории вкладчиков в сберегательных кассах города необходимо провести случайную повторную выборку лицевых счетов. Считая распределение размера вклада нормальным со средним квадратическим отклонением 150 руб., найти доверительный интервал для оценки среднего размера вклада с надежностью γ = 0,9. Известно = 1000.

Задание 9. Для каждой из приведенных ниже выборок (предполагается, что выборки получены из двумерных генеральных совокупностей (X, Y), имеющих нормальное распределение): а) построить корреляционное поле; б) вычислить выборочный коэффициент линейной корреляции и проверить его значимость при ; в) найти уравнение прямых линий регрессии Y  на X и X на Y, построить их графики:

X	10	15	20	25	30
Y	22	35	70	75	102

Вариант: 11

Задание 1. Найти изображение следующих функций:

а) ; б) .

Задание 2. По данному графику оригинала найти:

а) изображение ступенчатой функции, используя теорему запаздывания;

б) изображение для периодической функции; в) изображение, используя преобразование Лапласа.

а) a1	б)
в)

.Задание 3. Восстановить оригинал по изображению : .

Задание 4. Найти оригинал, учитывая, что изображения представляются в виде суммы элементарных дробей: .

Задание 5. Средствами операционного исчисления найти частные решения дифференциальных уравнений при указанных начальных условиях: а) б)

Задание 6. При установившемся технологическом процессе происходит в среднем 10 обрывов нити на 100 веретен в час. Найти закон распределения, функцию распределения и математическое ожидание случайного числа обрывов нити в течение часа среди трех веретен, работающих независимо друг от друга.

Задание 7. Для данных выборок определить выборочное среднее , выборочную дисперсию , «исправленную» выборочную дисперсию , моду Mo, медиану Me, размах R. Для a) составить вариационный и статистический ряды; для б) найти эмпирическую функцию распределения; для в) построить гистограмму и полигон, эмпирическую функцию распределения .

а) 3, 2, 4, 2, 4, 5, 3, 6, 7, 3.

б)	xi	1	5	9	13	17	21	22
	ni	6	4	5	8	2	4	4

в)	xi	[0; 7)	[7; 14)	[14; 21)	[21; 28)
	ni	3	1	1	2

Задание 8. Методом случайной повторной выборки было взято для проверки на вес 200 деталей. В результате проверки установлено, что распределение веса деталей можно считать нормальными со средним квадратическим отклонением 4 г; средний вес деталей 30 г. С надежностью 0,9544 требуется определить интервал, в котором находится средний вес деталей в генеральной совокупности.

Задание 9. Для каждой из приведенных ниже выборок (предполагается, что выборки получены из двумерных генеральных совокупностей (X, Y), имеющих нормальное распределение): а) построить корреляционное поле; б) вычислить выборочный коэффициент линейной корреляции и проверить его значимость при ; в) найти уравнение прямых линий регрессии Y  на X и X на Y, построить их графики:

X	5	10	15	20	25
Y	10	26	28	47	53