Вариант: 5

Задание 1. Найти изображение следующих функций:

а) ; б) .

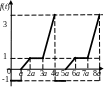
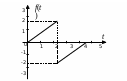
Задание 2. По данному графику оригинала найти:

а) изображение ступенчатой функции, используя теорему запаздывания;

б) изображение для периодической функции; в) изображение, используя преобразование Лапласа.

а)	б)
в)

.Задание 3. Восстановить оригинал по изображению : .

Задание 4. Найти оригинал, учитывая, что изображения представляются в виде суммы элементарных дробей: .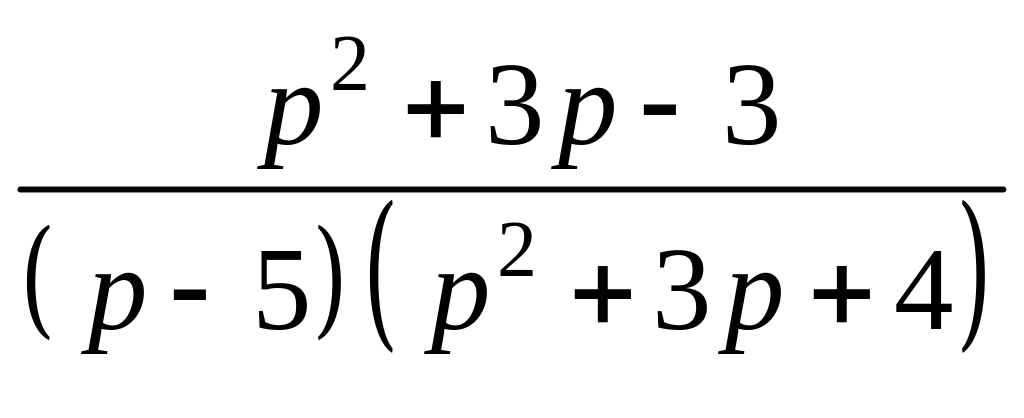

Задание 5. Средствами операционного исчисления найти частные решения дифференциальных уравнений при указанных начальных условиях: а) б)

Задание 6. Из пяти гвоздик две белые. Составить закон распреде­ления и найти функцию распределения случайной ве­личины, выражающей число белых гвоздик среди двух одновременно взятых. Вычислить .

Задание 7. Для данных выборок определить выборочное среднее , выборочную дисперсию , «исправленную» выборочную дисперсию , моду Mo, медиану Me, размах R. Для a) составить вариационный и статистический ряды; для б) найти эмпирическую функцию распределения; для в) построить гистограмму и полигон, эмпирическую функцию распределения .

а) 2, 5, 7, 6, 8, 3, 1, 5, 7, 5.

б)	xi	8	10	12	14	16	18	20
	ni	2	5	4	6	10	6	7

в)	xi	[0; 4)	[4; 8)	[8; 12)	[12; 16)	[16; 20)
	ni	2	4	1	3	4

Задание 8. Для стада из 100 голов методом случайной повторной выборки установлен средний годовой привес скота – 200 кг. Определить с надежностью 0,85 возможные пределы годового привеса скота, считая, что годовой привес распределен по нормальному закону, а среднее квадратичное отклонение равно 50 кг.

Задание 9. Для каждой из приведенных ниже выборок (предполагается, что выборки получены из двумерных генеральных совокупностей (X, Y), имеющих нормальное распределение): а) построить корреляционное поле; б) вычислить выборочный коэффициент линейной корреляции и проверить его значимость при ; в) найти уравнение прямых линий регрессии Y  на X и X на Y, построить их графики:

X	20	25	30	35	40
Y	100	118	123	130	145

Вариант: 6

Задание 1. Найти изображение следующих функций:

а) ; б) .

Задание 2. По данному графику оригинала найти:

а) изображение ступенчатой функции, используя теорему запаздывания;

б) изображение для периодической функции; в) изображение, используя преобразование Лапласа.

а)	б)
в)

.Задание 3. Восстановить оригинал по изображению : .

Задание 4. Найти оригинал, учитывая, что изображения представляются в виде суммы элементарных дробей: .

Задание 5. Средствами операционного исчисления найти частные решения дифференциальных уравнений при указанных начальных условиях: а) б)

Задание 6. Среди 15 собранных агрегатов 6 нуждаются в дополни­тельной смазке. Найти закон распределения, функцию распределения и математическое ожидание числа агрегатов, нуждающихся в дополнительной смазке, среди пяти наудачу отобранных из общего числа.

Задание 7. Для данных выборок определить выборочное среднее , выборочную дисперсию , «исправленную» выборочную дисперсию , моду Mo, медиану Me, размах R. Для a) составить вариационный и статистический ряды; для б) найти эмпирическую функцию распределения; для в) построить гистограмму и полигон, эмпирическую функцию распределения .

а) 1, 3, 8, 8, 9, 5, 2, 3, 4, 8.

б)	xi	7	10	13	16	19	22	23
	ni	6	1	7	10	6	4	2

в)	xi	[0; 3)	[3; 6)	[6; 9)	[9; 12)	[12; 15)
	ni	2	4	4	1	3

Задание 8. Результаты 10 измерений емкости конденсатора дали следующие отклонения от номинального значения (пкФ): 5,4; -13,9; -11,0; 7,2; -15,6; 29,2; 1,4; -0,3; 6,6; -9,9. Найти 90 %-ный доверительный интервал для дисперсии и среднего квадратичного отклонения, предполагая, что генеральная совокупность имеет нормальное распределение.

Задание 9. Для каждой из приведенных ниже выборок (предполагается, что выборки получены из двумерных генеральных совокупностей (X, Y), имеющих нормальное распределение): а) построить корреляционное поле; б) вычислить выборочный коэффициент линейной корреляции и проверить его значимость при ; в) найти уравнение прямых линий регрессии Y  на X и X на Y, построить их графики:

X	10	15	20	25	30
Y	16	20	30	48	56