Контрольная работа по Математике Преподаватель: ст. преподаватель Шувалова Л.Е.

Курс: Второй Семестр: III Специальность: МАХП (СПО)

Заочное отделение Группа: 2224

Вариант определить по двум последним цифрам номера зачетной книжки

Вариант: 1

Задание 1. Найти изображение следующих функций:

а) ; б) .

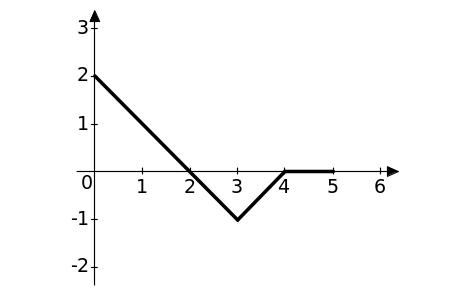
Задание 2. По данному графику оригинала найти:

а) изображение ступенчатой функции, используя теорему запаздывания;

б) изображение для периодической функции; в) изображение, используя преобразование Лапласа.

а)	б)
в f(t) t )

.Задание 3. Восстановить оригинал по изображению : .

Задание 4. Найти оригинал, учитывая, что изображения представляются в виде суммы элементарных дробей: .

Задание 5. Средствами операционного исчисления найти частные решения дифференциальных уравнений при указанных начальных условиях: а) б)

Задание 6. Контрольная работа состоит из трех вопросов. На каж­дый вопрос приведено четыре ответа, один из которых пра­вильный. Найти закон распределения, функцию распределения и математическое ожидание числа пра­вильных ответов при простом угадывании.

Задание 7. Для данных выборок определить выборочное среднее , выборочную дисперсию , «исправленную» выборочную дисперсию , моду Mo, медиану Me, размах R. Для a) составить вариационный и статистический ряды; для б) найти эмпирическую функцию распределения; для в) построить гистограмму и полигон, эмпирическую функцию распределения .

а) 7, 3, 3, 6, 4, 5, 1, 2, 1, 3.

б)	xi	11	13	15	17	19	21	23
	ni	2	4	8	12	16	10	3

в)	xi	[0; 4)	[4; 8)	[8; 12)	[12; 16)	[16; 20)	[20; 24)
	ni	1	1	3	2	1	1

Задание 8. Для определения среднего возраста учащихся возраста учащихся одного учебного заведения методом случайной повторной выработки обследовано 200 чел, в результате чего установлено, что средний возраст учащихся составляет 19 лет.

Полагая дисперсию равной 6,25 и считая распределение возраста учащихся нормальным, определить с надежностью 0,99 возможные пределы среднего возраста учащихся.

Задание 9. Для каждой из приведенных ниже выборок (предполагается, что выборки получены из двумерных генеральных совокупностей (X, Y), имеющих нормальное распределение): а) построить корреляционное поле; б) вычислить выборочный коэффициент линейной корреляции и проверить его значимость при ; в) найти уравнение прямых линий регрессии Y  на X и X на Y, построить их графики:

X	10	15	20	25	30
Y	8	26	28	44	59

Вариант: 2

Задание 1. Найти изображение следующих функций:

а) ; б) .

Задание 2. По данному графику оригинала найти:

а) изображение ступенчатой функции, используя теорему запаздывания;

б) изображение для периодической функции; в) изображение, используя преобразование Лапласа.

а)	б)
в)

.Задание 3. Восстановить оригинал по изображению : .

Задание 4. Найти оригинал, учитывая, что изображения представляются в виде суммы элементарных дробей: .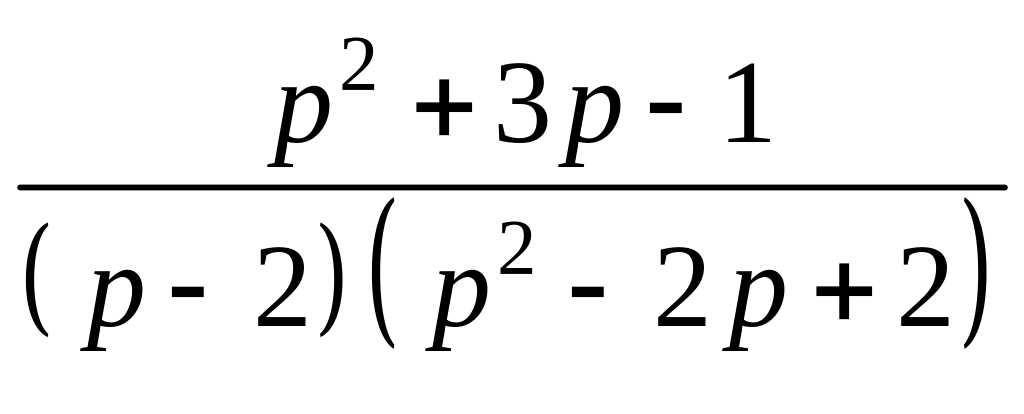

Задание 5. Средствами операционного исчисления найти частные решения дифференциальных уравнений при указанных начальных условиях: а) б)

Задание 6. В среднем по 10% договоров страховая компания вы­плачивает страховые суммы в связи с наступлением страхового случая. Найти закон распределения, функцию распределения и математическое ожидание чис­ла таких договоров среди наудачу выбранных четырех.

Задание 7. Для данных выборок определить выборочное среднее , выборочную дисперсию , «исправленную» выборочную дисперсию , моду Mo, медиану Me, размах R. Для a) составить вариационный и статистический ряды; для б) найти эмпирическую функцию распределения; для в) построить гистограмму и полигон, эмпирическую функцию распределения .

а) 6, 1, 4, 8, 5, 7, 2, 5, 7, 6.

б)	xi	12	14	16	18	20	22	23
	ni	3	5	9	10	8	7	4

в)	xi	[0; 3)	[3; 6)	[6; 9)	[9; 12)	[12; 15)	[15; 18)
	ni	4	1	2	3	3	1

Задание 8. Производится методом случайной повторной выборки обследование возраста читателей одной библиотеки. Сколько карточек необходимо взять для обследования, чтобы с вероятностью 0,99 можно было бы утверждать, что выборочная средняя отклоняется от генеральной средней не более чем на год? Среднее квадратичное отклонение принять равным 5 годам. Считать распределение возраста читателей нормальным.

Задание 9. Для каждой из приведенных ниже выборок (предполагается, что выборки получены из двумерных генеральных совокупностей (X, Y), имеющих нормальное распределение): а) построить корреляционное поле; б) вычислить выборочный коэффициент линейной корреляции и проверить его значимость при ; в) найти уравнение прямых линий регрессии Y  на X и X на Y, построить их графики:

X	20	25	30	35	40
Y	8	22	26	41	50