Энергетический спектр случайного процесса.
Неслучайная функция
имеющая размерность мощности на единицу полосы частот, называется спектральной плотностью мощности или энергетическим спектром стационарного случайного процесса. Введение энергетического спектра вместо спектральной плотности амплитуд является обобщением гармонического анализа на случайные процессы.
Более строго энергетический спектр стационарного случайного процесса определяется теоремой Хинчина-Винера, согласно которой энергетический спектр и корреляционная функция являются парой преобразования Фурье:
Следовательно, энергетический спектр стационарного случайного процесса является обычным амплитудным спектром корреляционной функции. Данное обстоятельство используется в настоящей лабораторной работе при нисхождении, энергетического спектра исследуемого случайного процесса. Для чего в начале определяется функция корреляции случайного процесса, а затем по ней вычисляется энергетический спектр.
Перечислим
основные свойства энергетического
спектра. Заметим что
,
как и
- чётная функция частоты и, кроме того,
неотрицательна. Из (18) при
получим
Следовательно,
средняя мощность процесса равна площади
под кривой его энергетического спектра,
деленной на
.
Это аналогично равенству Парсеваля для
детерминированных процессов.
Для
спектральной плотности средней мощности
случайного процесса при
из (17) получим
т.е. она равна площади под кривой его корреляционной функции
«Белый» и «окрашенный» шум.
Прохождение случайного процесса через линейные и нелинейные системы.
Канал передачи информации по определению – линейная система (линейный четырёхполюсник).
Канал передачи информации – четырёхполюсник (линейный), к которому предъявляется ряд требований.
Линейный четырёхполюсник – это такой четырёхполюсник, которого в спектре выходного сигнала y(t) не имеется частотных составляющих, которые не было в спектре входного сигнала x(t). В нелинейном четырёхполюснике в y(t) появляются частотные составляющие, которых не было во входном сигнале.
Любой четырёхполюсник обладает инерционными свойствами. Различают инерционные и безинерционные четырёхполюсники.
В
идеале
– это условие не обязательно для
линейного четырехполюсника.
Четырехполюсник характеризуется:
Статический коэффициент передачи по частоте – k(j)
Импульсная переходная характеристика – g(τ)
Спектр на выходе делим на спектр на входе.
Искажения ФЧХ определяется неравномерностью группового времени замедления (ГВЗ).
Импульсно-переходная характеристика – это реакция четырехполюсника на импульс, представляющий собой функцию Дирака (дельта импульс).
k(j) и g(τ) – однозначно жестко связаны законом Винера-Колмогорова.
Так как характеристики жёстко связаны, необходимо знать хотя бы одну из них.
Пусть на входе случайный процесс x(t), который представляет белый шум.
x(t) со спектральной плотностью N0 =const.
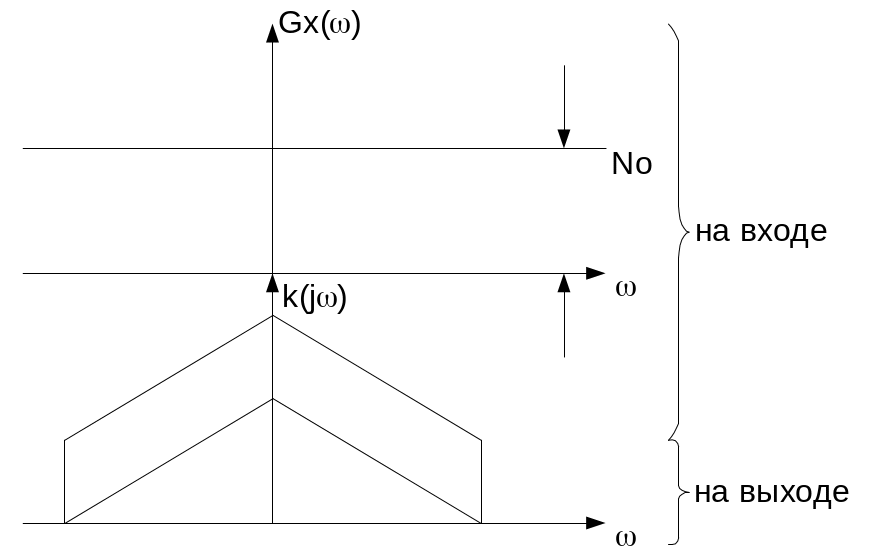
С точностью до масштабного коэффициента выход повторяет вход.
Ву(τ) – можно найти
Py – мощность процесса
Δτу – интервал корреляции
Δτу ≠ 0 – не дельта функция
Белый шум с нормальным законом распределения.
Если k(jw) – равномерный в определенной полосе частот, то на выходе энергетический спектр Gy(w) будет равномерным, а закон распределения нормальным. Следовательно, шум будет окрашенным, но будет являться гауссовским.
Процесс на выходе y(t) можно найти известным традиционным способом – интеграл Дюамеля:
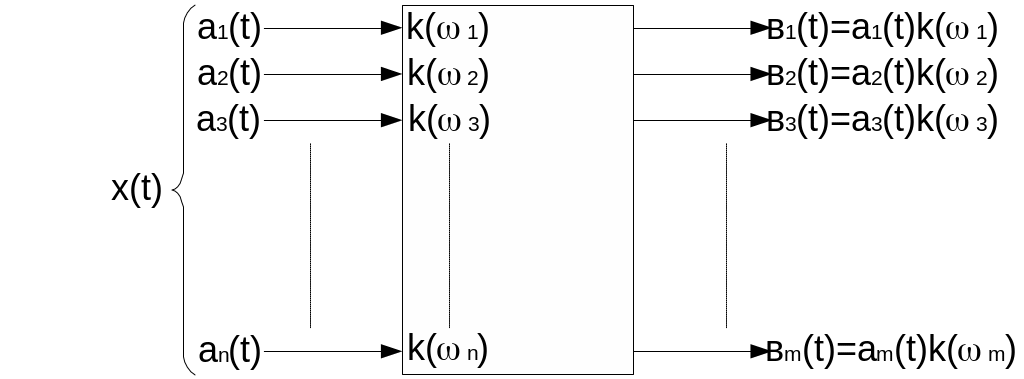
Если на входе четырехполюсника одновременно действует m случайных процессов, которые линейно независимые (ортогональны), то y(t) будет так же представлять собой сумму ортогональных процессов (Пример – многоканальные системы по одной направляющей).
Если эти процессы на входе не ортогональны (линейно зависимые, т.е. у всех различные законы распределения). При m→∞ процесс y(t) нормализуется (а в пределе может стать шумом).