14. Спектры сигналов при импульсных видах модуляции.

Теорема Котельникова лежит в основе любой цифровой системы.

При рассмотрении процесса дискретизации можно видеть, что при (равномерная дискретизация), сигнал – амплитудно-импульсный (амплитудно-импульсная модуляция, АИМ)

Импульсная несущая

АИМ

Название модуляции (аналоговая и импульсная) дают по виду несущей. У импульсной несущей можно менять , получим широтно-импульсную модуляцию (ШИМ) Если , то , получаем частотно-импульсную модуляцию (ЧИМ). Если , получаем фазово-импульсную модуляцию (ФИМ).

Т.к. , то это – индивидуальные импульсные несущие. Импульсная несущая и ее составляющие ортогональны.

Спектр импульсно-модулированных сигналов определяется спектром импульсных несущих. Независимо от вида модуляции спектр импульсно-модулированных сигналов есть симметричный спектр импульсной последовательности (т.е. несущей)

Модулированное колебание

Особенностью является спектр при АИМ, симметричный, относительно любой модулирующей составляющей, кроме нулевой. А спектр аналога модулированного сигнала определяется характером несущей составляющей.

15. Теоремы о спектрах.

Приведем теперь без доказательства, несколько теорем о спектрах, выражающие основные свойства преобразования Фурье.

1. Теорема сложения. Спектр суммы нескольких сигналов равен сумме спектров этих сигналов.

2. Теорема запаздывания. Спектральная плотность сигнала полученного при сдвиге сигнала по оси времени на , определяется выражением

т.е. сдвиг функции по оси времени приводит к появлению фазового сдвига для всех частотных составляющих, равного .

3. Теорема смещения. Если - спектр функции , то спектру 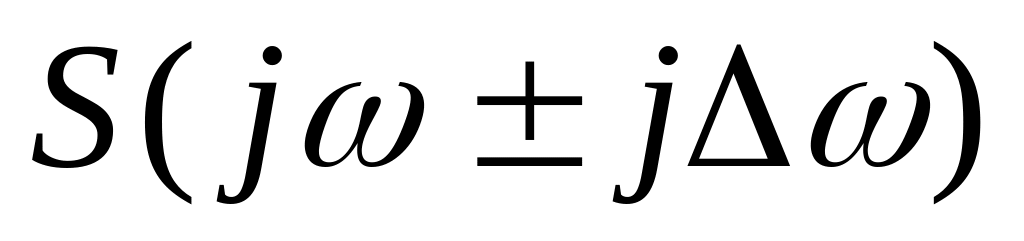полученному путем сдвига исходного спектра по оси частот на величину 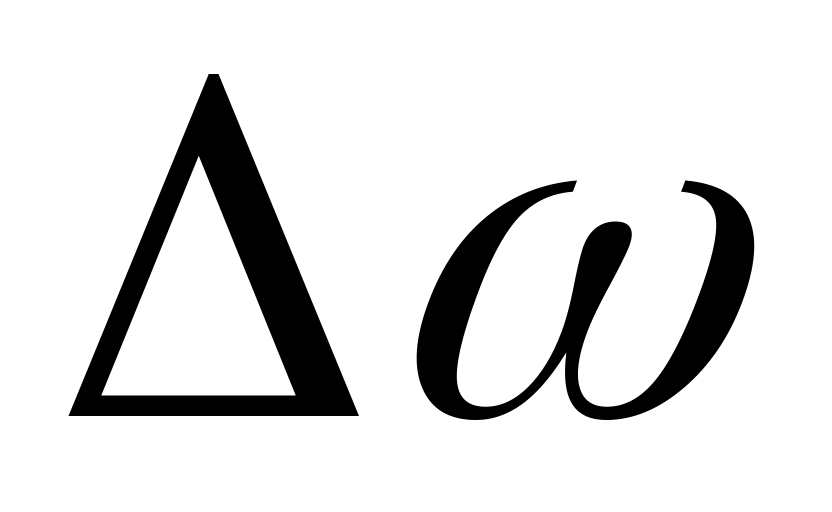, соответствует функция

4. Теорема о спектрах производной и интеграла. Спектры производной и интеграла от функции определяются выражениями

5) Теорема о спектре произведения. Спектр произведения двух функций S₁(t) и S₂(t) определяется операцией свертки их спектров:

16. Сигналы и помехи как случайные процессы.

Случайными процессами называют процессы, которые математически описываются случайными функциями времени. Случайной называется функция, значения которой при каждом значении аргумента являются случайными величинами.

Случайная функция времени , описывающая случайный процесс, в результате опыта принимает ту или иную конкретную форму , неизвестную заранее

Любую функцию можно представить конечным числом точек, отстоящих на интервал Δt:

- длительность сигнала.

Номера уровней квантования можно передавать в десятичной системе счисления. Удобно выбрать двоичную систему счисления, которая является вероятностной.

В современных цифровых системах используется двоичное кодирование, т.е. номера сигналов можно передавать как цифровые (численные) последовательности. В групповом канале последовательности всех каналов образуют непрерывную последовательность

Помеха по определению – дискретный или аналоговый процесс. Разницей между сигналом и помехой нет, т.е. они описываются случайной функцией времени. Но разницы нет только в этом смысле.

– случайные процессы.

В зависимости от того, какие значения принимает случайный процесс в моменты времени , случайные процессы подразделяют на дискретные и непрерывные.

- коэффициент взаимной корреляции

- коэффициент различимости

ФМ

АМ

Многофазная ЧМ

- ряд Котельникова лежит в основе систем передачи информации с временным разделением.