
- •Теория передачи сигналов (задачи, основные понятия, определения).
- •Обобщенная модель системы передачи информации, основные параметры.
- •Помехи и искажения в канале связи.
- •Сигналы и их формирование.
- •Кодирование и модуляция.
- •Достоверность и скорость передачи.
- •Модели сигналов и помех.
- •Тригонометрический ряд Фурье.
- •Амплитудно-фазовое представление ряда Фурье.
- •Аналитический сигнал.
- •Вычисление сигнала через спектральные и временные характеристики.
- •Функция отсчетов sin(X)/X и ее свойства.
- •Спектры сигналов при аналоговых видах модуляции.
- •Спектры сигналов при импульсных видах модуляции.
- •Импульсная несущая
- •Теоремы о спектрах.
- •Сигналы и помехи как случайные процессы.
- •Флуктуационная помеха (статистические и энергетические свойства)
- •Функция корреляции и ее свойства.
- •Энергетический спектр случайного процесса.
- •«Белый» и «окрашенный» шум.
- •Прохождение случайного процесса через линейные и нелинейные системы.
- •Понятие ширины энергетического спектра и интервала корреляции.
- •Основные типы задач приема сигналов.
- •Количественные критерии.
- •Прием сигналов, как статистическая задача.
- •Оптимальный прием сигналов – статистические критерии.
- •Критерий Неймана-Пирсона.
- •Оптимальный корреляционный приемник.
- •Прием сигналов методом синхронного повторения.
- •Комплексный ряд Фурье.
- •Временное представление сигналов и помех. Теорема о дискретизации. Ряд Котельникова.
- •Интеграл Фурье.
- •Равенство Парсеваля. Понятие ширины спектра.
- •Разложение сигналов на элементарные. Обобщенный ряд и коэффициенты Фурье.
- •Случайные процессы (способы задания, характеристики, параметры).
- •Оптимальный прием сигналов на согласованный фильтр.
- •Автокорреляционный прием.
- •Энтропия источника и ее свойства.
- •Энтропия непрерывного источника.
- •Количественная мера информации.
- •Условная энтропия.
- •Скорость передачи и пропускная способность.
- •43.Геометрическая модель системы передачи информации.
- •Оптимальный прием непрерывных сигналов.
- •Принцип помехоустойчивого кодирования.
- •Геометрическая модель сигналов, помех и канала.
- •Интегральный прием.
- •Циклический код.
- •Рекуррентный код.
- •Критерий среднего риска.
- •Статистические критерии оптимального приема, решающее устройство.
- •Стационарные случайные процессы.
- •Эргодическая теорема.
- •Корреляционный прием.
Геометрическая модель сигналов, помех и канала.
Г еометрическое
представление сигналов и помех.
еометрическое
представление сигналов и помех.
Сигнал
и помеху можно представить как вектор.
При геометрическом представлении
кодированных сигналов. Широко use
n-мерное
пространство в Неевклидовой метрике.
Расстояние в этом пространстве
определяется по алгоритму
![]() ,
n-
число элементов комбинации данного
кода, а xi
и
yi
–значения соответствующих разрядов.
Геометрической моделью n
- значного двоичного кода является
n-мерный
куб с ребром = 1, каждая из вершин которого
представляет одну из возможных комбинаций.
000,001,010,100,101,110,011,111 Расстояние -
,
n-
число элементов комбинации данного
кода, а xi
и
yi
–значения соответствующих разрядов.
Геометрической моделью n
- значного двоичного кода является
n-мерный
куб с ребром = 1, каждая из вершин которого
представляет одну из возможных комбинаций.
000,001,010,100,101,110,011,111 Расстояние -![]() .
Кодированный сигнал в виде n-мерного
куба.
.
Кодированный сигнал в виде n-мерного
куба.
Удобной формой представления сигналов и помех является геометрическая форма.Действительно, сигнал в сигнальном пространстве может быть представлен совокупностью чисел (число отчетов, гармоник).
n →x1, x2,……..xm Аналогично можно представить и помеху.В общем случае:

Действует аддитивная помеха x(t)=S(t)+W(t)
Если
под воздействием помехи результирующий
вектор, содержащий xi,
не пересекает пространство сигнала
x(t)
![]() ,
то ошибки нет. Если пересекает, то
появляется ошибка при приёме.
,
то ошибки нет. Если пересекает, то
появляется ошибка при приёме.
Если помеха аналоговая (белый шум) с произвольной амплитудой и фазой, то в сигнальном пространстве это будет круг (на плоскости), иначе будет шар, если m величин.
Если
попадается на границу
![]() ,
то повторяет передачу.
,
то повторяет передачу.
Один из важных параметров – угол α12 между векторами.
![]()
![]()
1) При ортогональной системе векторов
![]()
![]()
2)
При
![]()
3)
При
![]()
![]() –
это
коэффициент корреляции, коэффициент
статистической связи.
–
это
коэффициент корреляции, коэффициент
статистической связи.
![]() –
изменяется
от –1 до 1 и определяет различимость
сигналов при различных видах модуляции.
–
изменяется
от –1 до 1 и определяет различимость
сигналов при различных видах модуляции.
![]()
![]()
П
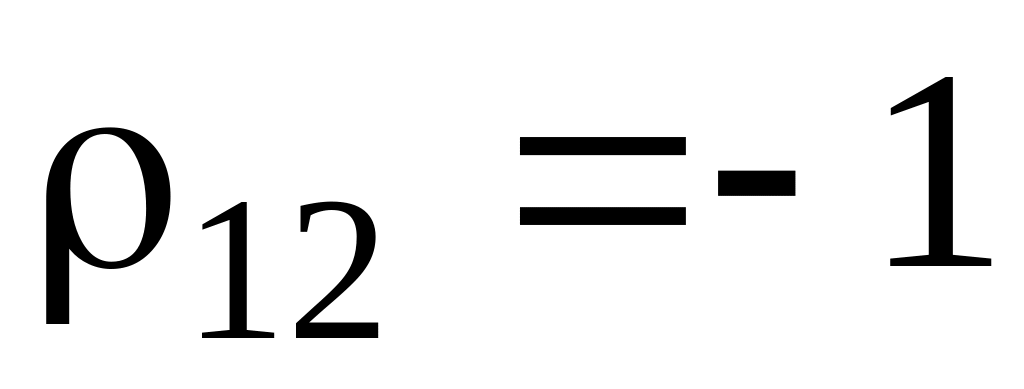 ри
ЧМ
ри
ЧМ
При ФМ


При АМ
![]() -
коэффициент различимости.
-
коэффициент различимости.
Интегральный прием.
Д
СВ,
помеха на выходе интегратора


Эфф.
полоса пропускания:
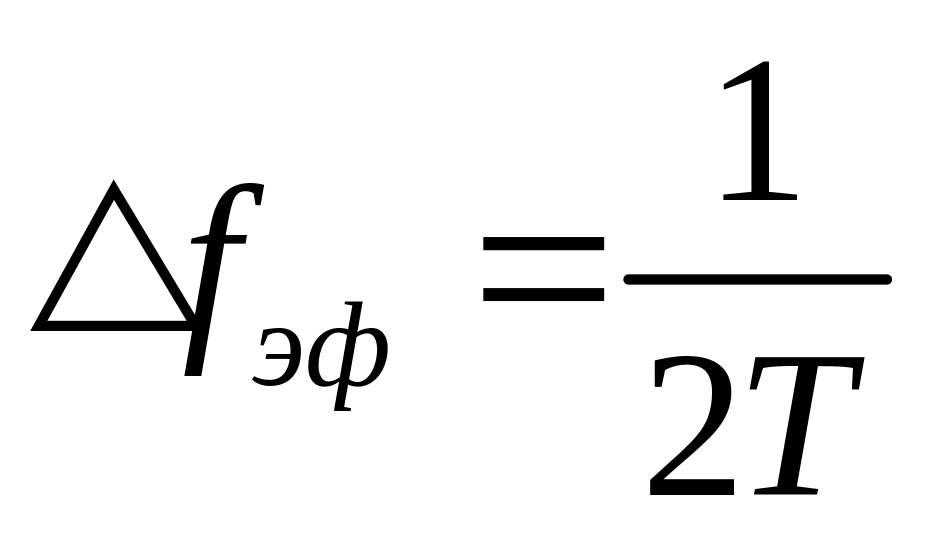 .
Если шум на выходе имеет мощность σ2
(в полосе F
> Δfэф),
мощность шума на выходе самого интегратора
< в F/Δfэф
.
Если шум на выходе имеет мощность σ2
(в полосе F
> Δfэф),
мощность шума на выходе самого интегратора
< в F/Δfэф


При интегральном приеме h2 > в N = T/Δτ = 2FT, N – число независимых значений помехи на
интервале (0; T). Это означает, что дискр-ое сумм-ие и интегр-ие обеспеч-ют одинаковый результат. Однако практически операция интегрирования осуществляется проще. В качестве интегратора может исп-ся RC-цепь.
В
ней С синхронно разряжается в конце
каждой посылки. Если на вход подают
радиоимпульс, то интегр-ие осущ-ся
коммутируемым разонатором, например,
колебательным контуром с высокой
добротностью.
Метод накопления суммированием или интегр-ем может быть осуществлён и при передаче одного и того же сигнала по нескольким независимым каналам (в к-ых действ. независим. помеха).
Циклический код.
Рекуррентный код.
Критерий среднего риска.
Является обобщением критерия идеального наблюдателя. Обобщение заключается в том, что учитываются последствия, к которым приводят ошибки разного рода. Ошибки можно выразить весовыми, стоимостными коэффициентами, которые приписываются к каждому из ошибочных решений – потери.
Правильному приёму приписываются либо отрицательные или нулевые значения потерь. Пусть Pk – вероятность ошибочного приёма сигнала Sk(L).
Lk – значение потерь.
Q=Lk Lk – риск для данного ошибочного решения.
Среднее значение ожидаемых потерь (средний риск):
![]()
Понятие среднего риска приводит к естественному критерию, к правилу решения. Правило должно минимизировать средний риск, учитывая среднюю вероятность правильного приёма.
![]()
1-й член: всегда положителен и не зависит от βk (от способа разбиения сигнала) следовательно минимум среднего риска обеспечивает такое разбиение пространства сигнала, при котором будет максимален второй член. Для этого каждую реализацию принятого сигнала необходимо относить к той области βl для которой подинтегральное выражение принимает наибольшее значение.
Правило критерия:
При
приходе сигнала x(t)
приёмник должен выдавать решение в
пользу сигнала Sl(t),
если для k≠l
выполняется условие
![]()
 Lk,
Ll
– потери.
Lk,
Ll
– потери.
Правило
принятия решения сводится к вычислению
отношения правдоподобия и сравнения с
пороговым значением
![]() .
.
- определяется априорными вероятностями сигнала и значением потерь.
Если Lk=Ll=L то критерий минимального среднего риска совпадает с критерием идеального наблюдателя.
“–”:
1. Необходимость знания априорных вероятностей сигнала.
2. Трудность объективного задания значения потерь (Баиевские критерии).
