Управление образования Могилевского облисполкома

Учреждение образования

«Бобруйский государственный

электротехнический колледж им. А. И. Черныша»

Практическая работа №3

на тему:1.Анализ электрического состояния цепи постоянного тока

методом наложения токов

2. Симулирование работы схемы в программе Multisim 12

по дисциплине: Теоретические основы электротехники

Учащийся Сыроватский Дмитрий Геннадьевич Курс __2__, группа _12С___ Специальность __Техник - электромеханик

Преподаватель__Рудой Игорь Александрович

Бобруйск 2012

В ариант 21

1 Определение тока во всех ветвях схемы на основании метода наложения.

По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов созданных каждой ЭДС в отдельности.

А) Определяем частные токи от ЭДС Е1, при отсутствии ЭДС Е2, т.е. рассчитываем цепь по данной схеме:

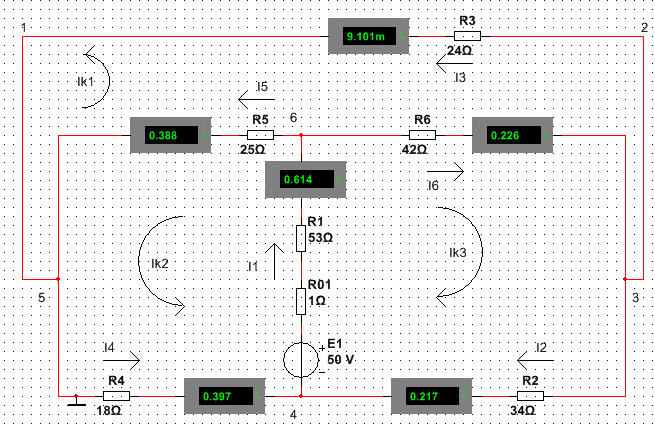
При расчетах используем метод контурных токов. Показываем направление частных токов от ЭДС Е1, и обозначаем буквой I. Исходные данные:

Таблица 1 Электрические данные схемы

E1 B	E2 B	R1 Oм	R2 Oм	R3 Oм	R4 Oм	R5 Oм	R6 Oм	r01 Oм	r02 Oм
50	30	53	34	24	18	25	45	1	1

А.1 Анализ электрического состояния цепи постоянного тока методом контурных токов.

К онтурный ток — это некоторая расчетная величина, которая одинакова для всех ветвей данного контура. Контурные токи на схе­ме обозначены I_k1, I_k2, I_k3.

Действительный ток в такой ветви определяется наложением контурных токов, т. е. равен алгебраической сумме контурных то­ков тех контуров, в которые эта ветвь входит.

1. В заданной схеме выбираем направления токов в ветвях (произвольно).

2. Намечаем независимые контуры и выбираем направление контурных токов.

3. Записывают систему уравнений: в левой части алгебраическая сумма Е входящих в контур, в правой — алгебраическая сумма падения напряжения на сопротивлениях входящих в этот контур, с учетом падения напряжения на сопротивлениях смежной ветви, определяемого по контурному току соседнего контура.

Запишем систему уравнений для рассматриваемой схемы

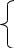
0 = I_k1 (R₃ + R₅ + R₆) – I_k2R₅ + I_k3R₆ (контур 1, 2, 3, 5)

E₁ = I_k2 (R₅ + R₄ + R₁+ r₀₁) – I_k1R₅ + I_k3(R₁+ r₀₁) (контур 5, 6, 4)

E₁ = I_k3 (R₁+ r₀₁ + R₂ + R₆) + I_k2(R₁+ r₀₁) + I_k1R₆ (контур 6, 4, 3)

Подставляем численные значения сопротивлений и ЭДС, получаем:

0 = I_k1 (24 + 25 + 42) – I_k225 + I_k342

50 = I_k2 (25 + 18 + 53 + 1) – I_k125 + I_k3(53+ 1)

50 = I_k3 (53 + 1 + 34 + 42) + I_k2(53+ 1) + I_k142

И ли:

0 = 91I_k1 – 25I_k2 + 42I_k3

50 = 97I_k2 – 25I_k1 + 54I_k3

50 = 130I_k3 + 54I_k2 + 42I_k1

Данная система уравнений будет иметь единственное решение только тогда, когда определитель составленный из коэффициентов при I_{k 1 - n} не будет равен нулю. Обозначим этот определитель знаком - Δ. Если этот определитель не равен нулю, то решаем дальше. Тогда каждый I_{k i} = Δ_i / Δ, где Δ_i - это определитель составленный из коэффициентов при I_{k 1 - n}, только значения коэффициентов в i - ом стольбце заменены на значения за знаком равенства в сисетеме уравнений, а Δ - это главный определитель

Г лавный определитель

Δ         =

91 -25 42 -25 97 54 42 54 130

=     516396

1 определитель , для вычисления I_k1.

Δ1       =

0 -25 42 50 97 54 50 54 130

=     4700

2 определитель , для вычисления I_k2.

Δ2       =

91 0 42 -25 50 54 42 50 130

=     205100

3 определитель , для вычисления I_k3.

Δ3       =

91 -25 0 -25 97 50 42 54 50

=     111900

Найдем решения данной системы уравнений. Согласно описанному выше методу, данная система уравнений имеет решения: I_k1 = Δ₁/Δ ≈ 0.0091А I_k2 = Δ₂/Δ ≈ 0.4А I_k3 = Δ₃/Δ ≈ 0.22А

Действительные токи:

I₁ = I_k2+ I_k3 = 0,62А

I₂ = I_k3 = 0,22А

I₃ = I_k1 = 0,0091А

I₄ = I_k2 = 0,4А

I₅ = I_k2- I_k1 = 0,39А

I₆ = I_k3 + I_k1 = 0,229А