
- •1 4. Моментом импульса твердого тела l относительно точки 0 называется векторная сумма моментов импульса материальных точек, составляющих данное тело, относительно той же точки 0:
- •50. Вектор индукции магнитного поля. Магнитное поле постоянного тока. Закон Био-Савара-Лапласа. Формула
- •Закон Био-Савара-Лапласа:
- •Расчет магнитной индукции на оси круглого проводника с током с помощью принципа суперпозиции:
- •Применение:
- •56. Применение теоремы о циркуляции для расчета магнитного поля внутри бесконечного соленоида и тороида.
- •Сила, действующая на проводник с током в магнитном поле:
Применение:
Теорема о циркуляции играет в магнитостатике приблизительно ту же роль, что и теорема Гаусса в электростатике. В частности, при наличии определённой симметрии задачи, она позволяет просто находить величину магнитного поля во всём пространстве по заданным токам[1]. Например, для вычисления магнитного поля от бесконечного прямолинейного проводника с током по закону Био — Савара — Лапласа потребуется вычислить неочевидный интеграл, в то время как теорема о циркуляции (с учётом осевой симметрии задачи) позволяет дать мгновенный ответ:
![]() .
.
56. Применение теоремы о циркуляции для расчета магнитного поля внутри бесконечного соленоида и тороида.
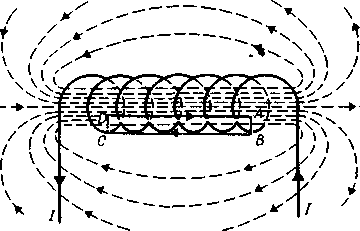 Соленоид
Соленоид
Для нахождения магнитной индукции ^ В выберем замкнутый прямоугольный контур ABCDA, как показано на рисунке. Циркуляция вектора В по замкнутому контуру ABCDA, охватывающему все N витков, согласно теореме равна
∫ Вl dl=μ0NI. ABCDA |
|
Интеграл по ABCDA можно представить в виде четырех интегралов: по АВ, ВС, CD и DA. На участках АВ и CD контур перпендикулярен линиям магнитной индукции и Вl = 0. На участке вне соленоида В = 0. На участке DA циркуляция вектора В равна В1 (контур совпадает с линией магнитной индукции); следовательно,
∫ Вl dl=μ0NI. DA |
|
Отсюда приходим к выражению для магнитной индукции поля внутри соленоида в вакууме:
B = μ0Nl/l |
|
 Тороид
Тороид
Магнитное поле, как показывает опыт, сосредоточено внутри тороида, вне его поле отсутствует. Линии магнитной индукции в данном случае, как следует из соображений симметрии, есть окружности, центры которых расположены по оси тороида. В качестве контура выберем одну такую окружность радиуса r. Тогда, по теореме о циркуляции: B2πr = μ0Nl. Откуда следует, что магнитная индукция внутри тороида (в вакууме) равна
B = μ0Nl/(2πr), |
|
где ^ N — число витков тороида. Если контур проходит вне тороида, то токов он не охватывает и В*2πr = 0. Это означает, что поле вне тороида отсутствует.
57. Электромагнитное воздействие токов. Закон Ампера. Сила, действующая на проводник с током в магнитном поле. Формула.
Закон
Ампера: Сила ![]() ,
с которой магнитное поле действует на
элемент
,
с которой магнитное поле действует на
элемент ![]() проводника
с током, находящегося в магнитном поле,
прямо пропорциональна силе тока
в
проводнике и векторному
произведению элемента
длины
проводника
на магнитную индукцию
проводника
с током, находящегося в магнитном поле,
прямо пропорциональна силе тока
в
проводнике и векторному
произведению элемента
длины
проводника
на магнитную индукцию ![]() :
:
![]()
Сила, действующая на проводник с током в магнитном поле:

58. Уравнения Максвелла для статических полей в вакууме. Формулы и физический смысл.
1)
![]() Поток электрической индукции через
замкнутую поверхность
Поток электрической индукции через
замкнутую поверхность ![]() пропорционален
величине свободного заряда, находящегося
в объёме
пропорционален
величине свободного заряда, находящегося
в объёме ![]() ,
который окружает поверхность
.
,
который окружает поверхность
.
2)
![]() Поток
магнитной индукции через
замкнутую поверхность равен нулю
(магнитные заряды не существуют).
Поток
магнитной индукции через
замкнутую поверхность равен нулю
(магнитные заряды не существуют).
3)
![]()
![]() Изменение потока
магнитной индукции, проходящего
через незамкнутую поверхность
,
взятое с обратным знаком, пропорционально
циркуляции электрического поля на
замкнутом контуре
Изменение потока
магнитной индукции, проходящего
через незамкнутую поверхность
,
взятое с обратным знаком, пропорционально
циркуляции электрического поля на
замкнутом контуре ![]() ,
который является границей поверхности
.
,
который является границей поверхности
.
4)
![]()
![]() Полный электрический
ток свободных зарядов и изменение потока
электрической индукции через незамкнутую
поверхность
,
пропорциональны циркуляции магнитного
поля на замкнутом контуре
,
который является границей поверхности
.
Полный электрический
ток свободных зарядов и изменение потока
электрической индукции через незамкнутую
поверхность
,
пропорциональны циркуляции магнитного
поля на замкнутом контуре
,
который является границей поверхности
.
59. Явление электромагнитной индукции. Закон Фарадея-Ленца. Формулировка. Явление самоиндукции, ЭДС индукции. Вывод формулы.
Явление электромагнитной индукции - явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.
Электромагнитная индукция была открыта Майклом Фарадеем 29 августа[источник не указан 299 дней] 1831 года. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.
Закон Фарадея-Ленца: электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром.
Явление самоиндукции, ЭДС индукции:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
60. Переменное электрическое поле. Ток Смещения. Определение. Уравнения Максвелла для переменных электромагнитных полей в вакууме. Формулы и физический смысл.
Переменное электрическое поле – это поле, порождающее магнитное поле.
Ток смещения - величина, прямо пропорциональная быстроте изменения электрической индукции
Уравнения Максвелла для переменных электромагнитных полей в вакууме:
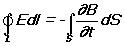 источниками электрического
поля могут быть не только электрические
заряды, но и изменяющиеся во времени
магнитные поля.
источниками электрического
поля могут быть не только электрические
заряды, но и изменяющиеся во времени
магнитные поля. Это уравнение показывает, что магнитные
поля могут возбуждаться либо движущимися
зарядами (электрическими токами), либо
переменными электрическими полями.
Это уравнение показывает, что магнитные
поля могут возбуждаться либо движущимися
зарядами (электрическими токами), либо
переменными электрическими полями. Теорема Остроградского-Гаусса
для поля D
Теорема Остроградского-Гаусса
для поля D Теорема
Остроградского-Гаусса для поля B
Теорема
Остроградского-Гаусса для поля B
