1. Механическое движение это перемещение тел или их частей друг относительно друга в пространстве с течением времени. Механическое движение относительно (не абсолютно): одно и то же тело может покоиться относительно одного тела отсчета и двигаться относительно другого.

Инерциальными называются системы отсчета, в которых выполняется закон инерции Галилея.

Закон инерции Галилея: тело, на которое не действуют другие тела, сохраняет состояние покоя или равномерного прямолинейного движения. Принцип относительности Галилея: механические явления во всех ИСО протекают одинаково .

Преобр координат галилея

И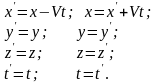 СО К неподвижна, относительно нее движется поступательно вдоль оси 0Х с постоянной скоростью V ИСО К’. В начальный момент времени начала координат обеих систем совпадают. Координаты точки М в системе К’ связаны с координатами в К следующими соотношениями:

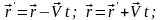
Преобразвоания скоростей галлилея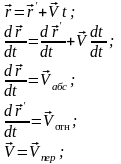

2 . Принцип относительности Эйнштейна: Физические явления протекают одинаково во всех инерциальных системах отсчета.

Преобразованиия лоренца формулы

Собственная длина стержня в системе К’, относительно которой стержень покоится:

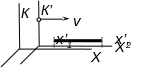Д лина стержня, измеренная в момент t₀ системе К, относительно которой стержень движется со скоростью V:

Сокращение длины происходит в направлении движения тела, а его поперечные размеры не меняются. Значит модель абсолютно твердого тела неприменима в релятивистской механике.

3 . Принцип постоянства скорости света: Скорость света в вакууме одинакова во всех инерциальных системах отсчета, не зависит от скорости движения источника и приемника света, является предельной скоростью распространения взаимодействий.

Преобразвонаия лоренца для корд и времени

Относительность одновременности событий

В точках х1 и х2 системы отсчета К происходят два события в моменты времени t1 и t2

В системе К’ этим событиям соответствуют моменты

Если в системе К события происходят одновременно t₁ = t₂, но в разных точках х₁≠х₂, то в К’ эти события не будут одновременными.

4. преобразования лоренца для скоростей

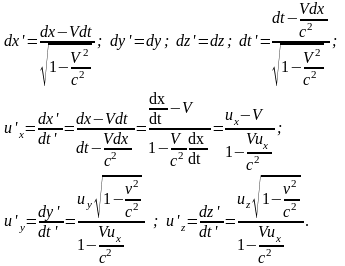
Обратные преобр скоростей

Постулаты: Принцип относительности Эйнштейна: Физические явления протекают одинаково во всех инерциальных системах отсчета

Принцип постоянства скорости света: Скорость света в вакууме одинакова во всех инерциальных системах отсчета, не зависит от скорости движения источника и приемника света, является предельной скоростью распространения взаимодействий

5.Модели: мат точка и абс тв тело. Материальная точка – это абстрактная модель реального тела нулевых размеров; то есть тела, размеры которого настолько малы (а<<L), что в рассматриваемом движении ими можно пренебречь (а=0) и считать, что всё вещество, из которого тело состоит, сосредоточено в точке. Поэтому нет смысла говорить о движении отдельных частей тела или о его вращении.

Числом степеней свободы i тела или системы тел называется число независимых переменных, определяющих положение этого тела или системы тел в пространстве.

Число степеней свободы материальной точки в трехмерном пространстве i = 3:

х = x(t), y = y(t), z = z(t);

При движении по поверхности i = 2:

x = x(t), y = y(t);

При движении вдоль линии i = 1:

s = s(t).

степени свободы системы мат точек

Материальные точки не связаны друг с другом: i = 3N.

Между материальными точками существует К жестких связей: i = 3N - К.

Пример: жесткий стержень длины

с двумя материальными точками на концах

i = 3N – К = 3.2 - 1 = 5

6.Способы описания движения мат точки: Векторный – задано значение и направление радиус-вектора материальной точки в каждый момент времени r=r(t). Координатный – задан закон изменения координат во времени x=x(t), y=y(t), z=z(t) . Траекторный – задано уравнение траектории, начало отсчета и закон движения по траектории s=s(t). Траекторией называется линия, по которой движется материальная точка

Мгновенной скоростью называется производная от радиус-вектора по времени. Вектор мгновенной скорости всегда направлен по касательной к траектории. Скорость измеряется в м/с. Существует предельная скорость – скорость света в вакууме с=3·10⁸ м/с.

Т ангенциальное ускорение - проекция вектора ускорения на касательную к траектории, равно производной от модуля скорости по времени

и 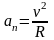отвечает за изменение скорости по величине. Нормальное ускорение - проекция вектора ускорения на нормаль к касательной к траектории, отвечает за изменение скорости по направлению.

R – радиус кривизны траектории.

7.Абсолютно твёрдое тело – это абстрактная модель реального тела, расстояние между любыми двумя точками которого остается неизменным; т.е. размеры и форма тела не меняются, деформаций нет (Δх<<x0).

Поступательным называется движение твердого тела, при котором все его точки движутся по одинаковым траекториям. Скорости всех точек одинаковы. Любая прямая, проведенная в теле,

движется параллельно самой себе.

Для определения положения твердого тела надо указать положение трех его точек, не лежащих на одной прямой. Число степеней свободы незакрепленного твердого тела:

i = 3N – К = 3.3 - 3 = 6

8. Простым вращательным называется такое движение твердого тела, при котором все его точки движутся по окружностям, расположенным в параллельных плоскостях, с центрами, находящимися на одной прямой, называемой осью вращения. Твердое тело при таком движении обладает одной степенью свободы i = 1, его угловое перемещение Δφ измеряется в радианах.

О бщим вращательным называется такое движение твердого тела, при котором все его точки движутся по концентрическим сферам вокруг общего центра. Такое движение можно описать с помощью углов Эйлера.(фи=фи от т и еще 2 угла так же). Пример: гироскоп в кардановом подвесе

9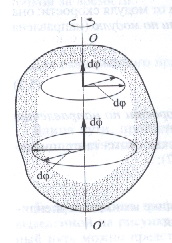 . Вектор бесконечно малого углового перемещения d(фи) направлен вдоль оси вращения по правилу правого винта, так что с конца вектора видно вращение против часовой стрелки.

Δφ - угловое перемещение тела за время Δt

Wср= Δφ\ Δt(рад\с;1\c; c в минус первой степени)

М гновенная угловая скорость – производная угла

поворота по времени

В ектор угловой скорости направлен по оси вращения в ту же сторону, что и вектор бесконечно малого углового перемещения , по правилу правого винта.

П ри вращении твердого тела с постоянной угловой скоростью ω = const, вращение называется равномерным и угол поворота линейно зависит от времени: φ(t)=φ₀+ωt . В этом случае ω называется круговой частотой вращения.

Период обращения – время одного оборота

v это линейная частота – число оборотов в секунду (1/с)

Угловым ускорением твердого тела называется производная угловой скорости по времени:

(рад/с² = 1/с²)

Вектор углового ускорения направлен по оси вращения в ту же сторону, что и угловая скорость, если она увеличивается, и в противоположную угловой скорости сторону, если она уменьшается.

С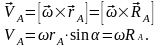 вязь линейной скорости точки вращающегося твердого тела с угловой скоростью вращения

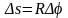
Связь углового перемещения твердого тела и линейного перемещения его точек

С вязь угловой скорости вращения твердого тела и линейной скорости его точек

10. Масса – скалярная величина, она определяет количество вещества в теле.

Масса является мерой инертности тела. Масса определяет гравитационное притяжение тел.Масса аддитивна, т.е масса тела равна сумме масс его частей.Масса тела не зависит от его движения.

М асса тела измеряется в кг ,ее величина определяется в сравнении с эталоном массы. Эталон сплав иридия с платиной размером 39х39мм.

Импульс материальной точки (количество движения) – векторная величина

С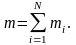 истемой материальных точек называется совокупность конечного их числа.

Масса системы N материальных точек:

Центр масс

11. Системой материальных точек называется совокупность конечного их числа. Импульс системы

С корость движения центра масс системы мат точек

И мпульс системы м.т. равен произведению массы системы на скорость движения ее центра масс:

12.

1 3. Моментом импульса материальной точки относительно геометрической точки 0 называется векторное произведение радиус-вектора м.т.

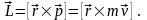
н 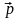а вектор ее импульса :

В ектор момента импульса перпендикулярен плоскости, в которой лежат радиус-вектор м.т. и вектор ее импульса .

Направление вектора определяется по правилу правого винта, а величина

Размерность момента импульса – кг^.м²/с.

М оментом импульса системы м.т. относительно точки 0 называется векторная сумма моментов импульса относительно той же точки всех м.т. системы:

L=cуммаLi=сумма[ri*pi]

М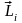 оментом импульса твердого тела L относительно точки 0 называется векторная сумма моментов импульса материальных точек, составляющих данное тело, относительно той же точки 0:

О севой момент импульса абсолютно твердого тела (момент импульса при вращении вокруг неподвижной оси):

1 4. Моментом импульса твердого тела l относительно точки 0 называется векторная сумма моментов импульса материальных точек, составляющих данное тело, относительно той же точки 0:

М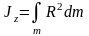 омент инерции является мерой инертности тела при вращательном движении.

Осевой момент инерции: или J_z = S m_i R_i²,

где R_i – расстояние точки m_i от оси вращения.

М омент инерции тела зависит от материала, размеров и формы тела, а также от расположения тела относительно оси, измеряется в кг^.м². Момент инерции аддитивная величина.

Теорема Гюйгенса-Штейнера:

М омент импульса твердого тела при вращении вокруг неподвижной оси выражается через осевой момент инерции:

Главные центральные оси инерции, относительно которых момент инерции имеет максимальное или минимальное значение, являются осями устойчивого вращения.

1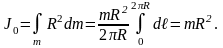 5. Момент инерции обруча относительно оси, проходящей через центр масс перпендикулярно плоскости, в которой лежит обруч:

1 6. Момент инерции диска относительно оси, проходящей через центр масс перпендикулярно плоскости диска:

1 7. Механической энергией системы называется сумма ее кинетической и потенциальной энергии:

П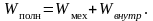 олная энергия системы тел равна сумме механической и внутренней энергии

При любых физических взаимодействиях энергия не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. Это фундаментальный закон природы.

1 8. Кинетическая энергия системы тел (энергия движения) измеряется той работой, которую может совершить система, двигаясь до полной остановки всех своих частей.

П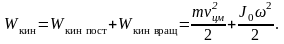 ри плоском движении а.т. тела кинетическая энергия равна сумме кинетических энергий поступательного и вращательного движения

1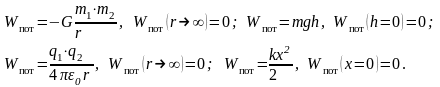 9. Потенциальная энергия системы (энергия взаимодействия тел) измеряется той работой, которую может совершить система, изменяя свою конфигурацию (взаимное расположение своих частей). Нормировкой потенциальной энергии называется выбор такой конфигурации системы, при которой ее потенциальная энергия принимается равной 0

20. Сила- векторная физическая величина являющаяся мерой взаимодействия тел

М оментом силы М относительно точки 0 называется векторное произведение радиус-вектора точки приложения силы на вектор силы . Вектор момента импульса перпендикулярен плоскости, в которой лежат радиус-вектор точки приложения силы и вектор силы, направлен по правилу правого винта. Его величина равна произведению модулей этих векторов на синус угла между ними. Размерность момента силы – Н^.м.

О севой момент силы

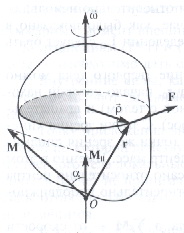
физ маятник

21. Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы

Р абота силы при поступательном движении:

измеряется в джоулях (1Дж = 1Н.1м).

М ощность силы – работа в единицу времени

измеряется в ваттах (1Вт = 1Дж/с).

Р абота при вращательном движении

М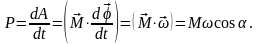 ощность при вращательном движении

22. Система тел или материальных точек называется изолированной, если на нее

не действуют внешние тела.

В изолированных системах тел сохраняются:

импульс;

момент импульса;

полная энергия.

Импульс системы тел или системы материальных точек сохраняется, если система изолирована.

Закон сохранения импульса является следствием однородности пространства.

У словия сохр импульса в неизолированных системах тел

В неизолированных системах есть внешние силы импульс сохраняется, если:

1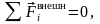 ) внешние силы скомпенсированы

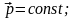тогда

2 ) внешние силы скомпенсированы вдоль одной из осей, тогда сохраняется проекция импульса на эту ось:

3) при кратковременных взаимодействиях (ударах, взрывах):

П римеры: Сохранение импульса системы тел: движущаяся платформа и вылетающий из орудия снаряд

И покоящиеся тележка. Рдо=0 Рпосле=Р2+Р1=0 Рдо=Рпосле=const

23. Закон сохранения момента импульса

Момент импульса системы тел или системы материальных точек сохраняется, если система изолирована.

У равнение моментов для системы тел:

В изолированной системе нет внешних сил

значит нет и моментов внешних сил

с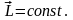 ледовательно и

Закон сохранения момента импульса является следствием изотропности пространства.

Условия сохранения момента импульса в неизолированных системах тел

М омент импульса неизолированных систем сохраняется, если

1 )моменты внешних сил относительно точки 0 скомпенсированы сохраняется момент импульса системы относительно этой точки:

2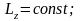 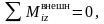) моменты внешних сил скомпенсированы относительно некоторой оси тогда сохраняется проекция момента импульса системы на эту ось:

3) при кратковременных взаимодействиях:

П римеры: Человек сидит на стуле, в руки взял гантели, сначала руки встороны, а потом к себе и крутится

24. Система тел называется консервативной, если в ней действуют только консервативные силы. Консервативные силы зависят от расстояния между взаимодействующими телами и не зависят от их скоростей. Консервативными являются упругие, гравитационные, кулоновские силы. Эти силы являются потенциальными, т.е. могут быть выражены через потенциальную энергию взаимодействия тел. Работа этих сил не зависит от формы траектории и равна убыли потенциальной энергии

Закон сохранения механической энергии: Механическая энергия системы тел или материальных точек сохраняется, если система во-первых, изолирована, а кроме того, во-вторых, консервативна.

Условие закона сохранения мех энергии в НИСО

В неизолированных неконсервативных системах механическая энергия сохраняется, если работа внешних сил равна нулю и работа внутренних неконсервативных сил равна нулю

2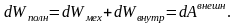 5. Полная энергия системы тел сохраняется, если система изолирована

В изолированной системе нет внешних сил

В неизолированной системе тел

п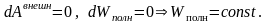 олная энергия сохраняется, если работа внешних сил равна нулю:

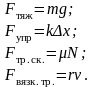
26. В законы динамики входят

I закон Ньютона: ИСО;

II закон Ньютона:

I II закон Ньютона:

И законы, определяющие свойства сил:

I закон: существуют системы отсчета, в которых тело, на которое не действуют другие тела, сохраняет состояние покоя или равномерного прямолинейного движения.

I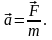 I закон: под действием силы тело приобретает ускорение прямо пропорциональное действующей силе, обратно пропорциональное массе тела и направленное по направлению силы:

I II закон:

Силы взаимодействия возникают парами, приложены к разным телам.

Равны по величине.

Направлены вдоль одной прямой.

Противоположны по направлению.

Имеют одинаковую физическую природу.

27. Основной закон динамики простого вращательного движения твердого тела

Jz – осевой момент инерции вращения вокруг оси Z

B угловое ускорение тела

M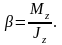 z сумма моентов сил приложенных к телу рассчитанных относительно оси вращения

28. Неизолированными называются системы тел, на которые действуют внешние тела.

I и III законы Ньютона не выполняются, так как силы инерции – внешние и не имеют сил противодействия, II закон:

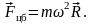
Центробежная сила инерции:

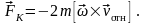
Кориолисова сила инерции:

2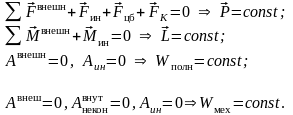 9. В НИСО нет изолированных систем. Поэтому выполняются частные законы сохранения:

39. Электрический заряд – это физическая скалярная величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.

Свойства: 1) существуют + и – заряды, одноименные отталкиваются, разноименные притягиваются

2) Дискретность: Любое заряженное тело содержит целое число электрических зарядов q=Ne

3) Инвариантность: Электроны движутся а величина заряда не меняется(в-на не зависит от скорости)

4) Закон сохранения электрического заряда. В электрически изолированной системе заряд не меняется.

Опыты Милликена: опыт по измерению элементарного эл-го заряда. В конденсатор вводили заряженные капельки масла и в определенный момент возникало состояние равновесия(неподвижности капельки)

4 0. Закон кулона: Сила взаимодействия точечных зарядов прямо пропорциональна произведению этих зарядов и обратно пропорциональна квадрату расстояния между ними.

Н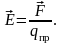 апряженностью электрического поля в некоторой точке называется векторная физическая величина, равная отношению силы, действующей на пробный заряд в данной точке поля, к величине этого пробного заряда:

Напряженность электрического поля измеряется в Н/Кл или В/м. Изображается силовыми линиями, касательные к которым совпадают с направлением вектора напряженности в данной точке поля. Силовые линии поля направлены по радиусам от положительного точечного заряда и по радиусам к отрицательному заряду.

Э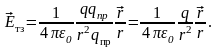 лектрическое поле создаваемое точечным зарядом

4 1. Принцип супер позиции: Если электрическое поле создается несколькими точечными зарядами, то напряженность этого поля равна векторной сумме напряженностей, создаваемых каждым точечным зарядом в отдельности:

Э лектрическое поле диполя

Электрический дипольный момент

Р асчет напр на оси диполя

42. Электри́ческий ди́польный моме́нт — векторная физическая величина, характеризующая электрические свойства системы заряженных частиц (распределения зарядов) в смысле создаваемого ею поля и действия на нее внешних полей.

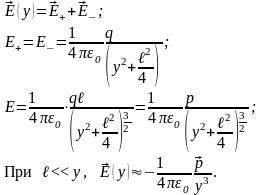
4 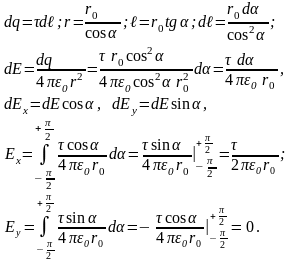3. линейная плотность заряда(кл\м)

44. Полное число силовых линий, проходящих через поверхность S, называется потоком вектора напряженности ФЕ через эту поверхность. Элементарный поток через малую площадку dS

n - единичный вектор нормали

к площадке dS.

Т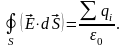 еорема Остроградского – гаусса: Поток вектора напряженности электрического поля через любую замкнутую поверхность равен суммарному заряду, заключенному внутри этой поверхности, деленному на :

4 8. Потенциал электростатического поля – скалярная физическая величина, равная отношению потенциальной энергии взаимодействия пробного заряда с зарядами, создающими поле в данной точке, к величине пробного заряда

П отенциальная энергия взаимодействия двух точечных зарядов при нормировке на бесконечность:

Потенциал электростатического поля, создаваемого точечным зарядом:

49. Связь между потенциалом и напряженностью электростатического поля. Формула. Силовые линии и эквипотенциальные поверхности. Циркуляция вектора напряженности электрического поля. Определение.

Связь между потенциалом и напряженностью электрического поля:

E_x dx + E_y dy + E_z dz = d где E_x, E_y, E_z - проекции вектора напряженности на оси системы координат. 

Силовые линии и эквипотенциальные поверхности:

Напряженность равна разности потенциалов U на единицу длины силовой линии.

Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью. Уравнение этой поверхности

Циркуляцией вектора напряженности называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L