После завершения расчета в диалоговом окне Результаты поиска решения и активации поля Сохранить найденное решение, нажав кнопку Ok, полученный вариант оптимального плана раскроя можно сохранить в виде файла, пример которого показан на рис. 7.5. Задача решена.

Рис. 7.5. Оптимальный план раскроя заготовок

Данные рис. 7.5 свидетельствуют о том, что в результате раскроя по оптимальному варианту можно изготовить семь комплектов деталей.

Для этого следует из заготовки L1 длиной 10,2 м вырезать по шесть деталей J1 и J2 длиной 0,37 и 0,12 м соответственно и одиннадцать деталей J4 длиной 0,66 м.

Заговку L2 длиной 15,1 м целесообразно разрезать на две детали J2 длиной 0,12 м, двадцать деталей J3 длиной 0,17 м и семнадцать деталей J4 длиной 0,66 м.

А из заготовки L3 длиной 7,3 м  получить по одной детали J1 и J3 длиной 0,37 и 0,17 м соответственно, шесть деталей J2 длиной 0,12 м и семь деталей J4 длиной 0,66 м.

Суммарные отходы металлопроката сотавят 1,66 м.

12. Выполните задание согласно вариантов, приведенных в табл. 7.1.

Таблица 7.1

Варианты заданий для раскроя металлопроката

Практическое занятие №8

Моделирование температурных полей при сварке

с использованием Ms Excel

Цель работы: Научиться моделировать температурные поля при сварке с использованием Ms Excel.

Оборудование, приборы и материалы: ПЭВМ, программа Ms Excel.

Общие положения

В Ms Excel ввод формул должен начинаться со знака = (равно). Все записи в формулах должны осуществляться латинскими буквами В формулах используются знаки: + (сложение),  (вычитание), * (умножение), / (деление), ^ (возведение в степень), а также специальные функции (кнопка Вставка функции на панели инструментов Стандартная). Для задания очередности операций используются круглые скобки ().

При выполнении вычислений по сложным формулам используется пошаговое вычисление.

При этом следует просмотреть значения различных частей сложной формулы, вычисляемые в соответствии с порядком действий.

За один раз может быть вычислена только одна ячейка.

В меню Сервис выберите пункт Зависимости формул и выполните команду Вычислить формулу .

Нажмите кнопку Вычислить, чтобы проверить значение подчеркнутой ссылки. Результат вычислений показан курсивом.

Если подчеркнутая часть формулы является ссылкой на другую формулу, нажмите кнопку Шаг с заходом, чтобы отобразить другую формулу в поле Вычисление. Нажмите кнопку Шаг с выходом, чтобы вернуться в предыдущую ячейку и формулу.

Продолжайте, пока каждая часть формулы не будет вычислена.

Чтобы снова увидеть вычисления, нажмите кнопку Начать сначала. Чтобы закончить вычисления, нажмите кнопку Закрыть.

Кнопка Шаг с заходом недоступна для ссылки, появляющейся в формуле вторично, и для формулы, ссылающейся на ячейку в отдельной книге.

Можно не использовать написание выражений сложных формул, а организовать вычисление отдельных ее фрагментов в различных ячейках рабочего листа с последующим их использованием для получения конечного результата.

Копирование формул осуществляется аналогично обычной процедуре копирования. При этом происходит автоматическое изменение адресации ячеек, то есть результат в очередной ячейке вычисляется для данных, полученных из новых ячеек. Если необходимо, чтобы адрес какой-то ячейки в формуле оставался неизменным (абсолютная ссылка), то перед буквой и цифрой адреса ячейки ставится знак $. Например, $С$23.

Построение графиков осуществляется по введенным в рабочую таблицу данным.

Щелчком указателя мыши по кнопке на панели инструментов вызываем Мастер диаграмм . В появившемся диалоговом окне Мастер диаграмм выбираем тип графика, например, График и его вид (см. рис. 8.1). После нажатия кнопки Далее устанавливаем положение переключателя Ряды в: строках или столбцах и, щелкнув кнопку в поле Диапазон, указываем на рабочем листе диапазон ячеек, содержащиих необходимые для построения графика данные (см. рис. 8.2). При этом после указания начальной ячейки с клавиатуры вводится символдиапазона  двоеточие (:) и указывается конечная ячейка диапазона.

Рис. 8.1. Вид диалогового окна Мастер диаграмм (шаг 1)

Рис. 8.2. Вид диалогового окна Мастер диаграмм (шаг 2)

После нажатия кнопки Далее вводим название графика, двух осей, выбираем линии сетки и нажимаем кнопку Далее. В появившемся новом диалоговом окне выбираем размещение созданного графика на отдельном или созданном листе и завершаем процедуру, нажав кнопку Готово.

Задание

Рассчитать и построить распределение температуры в поперечном сечении сварного соединеия пластины из низколегированной стали тол-щиной через в сечении с координатами относительно движущегося сварочного источника , . Мощность сварочного источника , скорость сварки . Теплофизические характеристики низколегированной стали соответствуют следующим параметрам:

• коэффициент температуропроводности ;

• коэффициент теплопроводности ;

• объемная теплоемкость .

Начальная температура свариваемой пластины .

Порядок выполнения работы

1. Принимаем сварочный источник как мощный быстродвижущийся линейный источник в бесконечной пластине, температурное поле которого можно описать уравнением вида

. (8.1)

2. Заносим в ячейки все исходные данные для расчета (см. пример на рис. 8.3).

Рис. 8.3. Вид рабочего листа с исходными данными

Запись формулы для расчета температурного поля осуществлен копированием выражения (8.1) и вставкой в рабочий лист содержимого буфера.

3. Программируем в Ms Excel расчет уравнения (8.1) по частям. Пример приведен на рис. 8.4.

Рис. 8.4. Вид рабочего листа с программой расчета

выражения (8.1) по частям

Алгоритм программирования состоит из последовательного определения следующих значений:

• Корня квадратного в знаменателе (8.1) в категориях Ms Excel в соответствии с рис. 8.4 будет иметь вид выражения в ячейке D16:

.

• Знаменателя (8.1)  ячейка D17:

.

• Показателя степени (8.1) ( ) при  ячейка D18:

.

• Показателя степени (8.1) ( ) при  ячейка Е18:

.

• Показателя степени (8.1) ( ) при  ячейка F18:

.

……………………………………………………………

…………………………………………………………….

…………………………………………………………….

• Показателя степени (8.1) ( ) при  ячейка M18:

.

• Приращения температуры в точке ,  ячейка D19:

.

• Приращения температуры в точке ,  ячейка E19:

.

• Приращения температуры в точке ,  ячейка F19:

.

……………………………………………………………

…………………………………………………………….

…………………………………………………………….

• Приращения температуры в точке ,  ячейка M19:

.

• Температуры в точке ,  ячейка D20:

.

• Температуры в точке ,  ячейка E20:

.

• Температуры в точке ,  ячейка F20:

.

……………………………………………………………

…………………………………………………………….

…………………………………………………………….

• Температуры в точке ,  ячейка M20:

.

4. Создаем рабочую таблицу данных для построения графика (см. рис. 8.5).

Рис. 8.5. Вид рабочего листа с рабочей таблицы данных

В ней строка № 23 компилирует данные строки № 8 (рис. 8.4), а строка № 24  строки № 20 (рис. 8.4).

5. Строим график, используя Мастер диаграмм, алгоритм применения которого описан выше (см. раздел Общие положения настоящей работы).

Пример построения графика распределения температуры приведен на рис. 8.6.

Рис. 8.6. Вид графика распределения температуры

6. Построить распределение температуры для тех же условий, но для скорости сварки v = 2 cм/с с отдельным графиком.

Практическое занятие №9 Изучение основ работы в системе Mathcad

Цель работы: Изучить основные приемы работы в системе Mathcad. Изучить интерфейс Mathcad 14, научиться запускать и завершать работу системы Mathcad,создавать документ, сохранять его, закрывать и открывать документ; научиться выполнять простейшие вычисления в среде Mathcad.

Оборудование, приборы и материалы: ПЭВМ, программа Mathcad 14.

Общие положення

Интерфейс Mathcad аналогичен интерфейсу других Windowsприложений.

Рабочее окно Mathcad

После запуска на экране появляется jкно приложения Mathcad 14 с пустым документом Безымянный: 1.

Рис. 9.1. Окно приложения Mathcad 14 с пустым документом Безымянный: 1

Оно имеет ту же структуру, что и большинство приложений Windows. Сверху вниз располагаются Заголовок окна, строка Главного меню (см. рис. 9.2, а), Стандартная панель инструментов (рис. 9.2, б), Панель инструментов форматирования (рис. 9.2, в) и Рабочий лист или Рабочая область документа (worksheet).

а

б

в

Рис. 9.2. Главное меню и панели инструментов Mathcad 14

Новый документ создается автоматически при запуске Mathcad. В самой нижней части окна находится строка состояния. Не забывая о сходстве редактора Mathcad с обычными текстовыми редакторами, интуитивно понятно назначение большинства кнопок на панелях инструментов.

Ниже перечислены пункты Главного меню Mathcad.

 кнопка раскрытия системного меню рабочего окна Mathcad.

 команды, связанные с созданием, открытием, сохранением, пересылкой по электронной почте и печатью на принтере файлов с документами.

 команды, относящиеся к правке текста (копирование, вставка, удаление фрагментов и т. д.).

 команды, управляющие внешним видом документа в рабочем окне Mathcad, а также команды создания файлов анимации.

 команды вставки различных объектов в документ.

 команды форматирования текста, формул и графиков.

 команды управления вычислительным процессом.

 команды символьных вычислений.

 команды расположения окон с различными документами на экране.

 команды вызова справочной информации и доступа к Центру документации.

Стандартная панель инструментов

Панели инструментов служат для быстрого выполнения наиболее часто применяемых команд (см. рис. 9.2).

Создать  создание документа на основе шаблона Normal (Обычный).

 открытие списка предлагаемых шаблонов документов.

Открыть  открытие файла.

Сохранить  сохранение файла.

Печать  печать файла.

Предварительный просмотр печати  просмотр подготовленного к печати документа.

Проверка орфографии — включение системы проверки правописания

Вырезать  вырезание объекта.

Копировать  копирование объекта.

Вставить — вставка объекта.

Отменить  отмена предыдущего действия (только при вводе текста или формул).

Вернуть  повторение отмененного действия.

Выровнять вдоль  выравнивание выделенной группы объектов по горизонтали.

Выровнять по высоте  выравнивание выделенной группы объектов по вертикали.

Вставить функцию  открытие диалогового окна со списком встроенных функций, служащего для их выбора и вставки.

Вставить единицы измерения  открытие диалогового окна со списком доступных единиц измерения, служащего для их выбора и вставки.

Подсчет  подсчет документа.

Вставка гиперссылки  открытие диалогового окна для вставки гиперссылки.

Вставить компонент  запуск мастера вставки в рабочий документ окна другого приложения, например, Ms Excel, Matlab и др.

Вставить  вставка различных объектов в рабочий документ окна.

Увеличить  список масштабных коэффициентов.

Справка  открытие окна справочной системы Mathcad.

Панель инструментов форматирования Mathcad содержит следующие инструменты.

Стиль  стиль для текста и формул.

Шрифт  шрифт для текста и формул.

Размер шрифта .

Полужирный  полужирное начертание.

Курсив  наклонное начертание.

Подчеркнутый  подчеркнутое начертание.

Выровнять влева  выравнивание текста по левому краю.

Выровнять по центру  выравнивание текста по центру.

Выровнять справа  выравнивание текста по правому краю.

Буллиты  вставка маркированного списка.

Нумерация  вставка нумерованного списка.

Верхний индекс  вставка символа с верхним индексом (надстрочный).

Нижний индекс  вставка символа с нижним индексом (подстрочный).

Помимо элементов управления, характерных для типичного текстового редактора, Mathcad снабжен дополнительными средствами для ввода и редактирования математических символов и уравнений. Настройка панели инструментов осуществляется командой Главного меню Вид > Панели инструментов (см. рис. 9.3).

Математическая панель инструментов со всеми дополнительными панелями показана на рис. 9.4.

Рис. 9.3. Настройка Панели инструментов

Рис. 9.4. Математическая панель инструментов

Ниже перечислены дополнительные панели математаческой панели инструментов. Номера соответствуют рис. 9.4.

1. Математика  вставка математических символов и операторов в документы.

2. Матрица  шаблоны матриц и матричных операций.

3. Калькулятор  шаблоны основных математических операций, цифр, знаков арифметических операций.

4. Греческая  буквы греческого алфавита.

5. График  шаблоны графиков.

6. Программирование  операторы, необходимые для создания программных модулей.

7. Логический  логические (булевы) операторы.

8. Исчисление  шаблоны дифференцирования, интегрирования, суммирования, пределов, градиента.

9. Вычисление  операторы присваивания значений и вывода результатов расчета.

10. Символьная  преобразования Лапласса, Фурье, Z-преобразование (прямые и обратные), замена переменных и др.

Щелчок мышью на любом из инструментов панелей приводит к вставке соответствующего этому инструменту символа или шаблона математической операции на место курсора в рабочем документе.

Построение и вычисление выражений

Перед началом работы на экране курсор имеет вид крестика. В момент ввода выражения курсор приобретает вид синего уголка, охватывающего вводимое выражение. В рабочем документе введите какие-либо буквенные выражения и присвойте им численные значения, как показано слева вверху на рис. 9.5. Имя выражения (все, что находится слева от оператора присваивания ) может состоять из латинских, рус-ских, греческих и других букв, а также цифр, знаков подчеркивания (_), штриха (‘), процента (%) и бесконечности ( ), вводимых с клавиатуры.

Рис. 9.5. Построение математических выражений

Имена переменных и функций не могут начинаться с цифры, знака подчеркивания, штриха, символа процента, не могут включать в себя пробелы. Символ бесконечности может бать только первым символом в имени.

Внимание!

Mathcad воспринимает прописные и строчные буквы как разные идентификаторы.

Mathcad не делает различий между именами переменных и функций. Если определить вначале функцию , а затем переменную , то окажется невозможным использовать функцию в последующих расчетах где-либо ниже определения .

Некоторые имена уже используются Mathcad для встроенных констант, единиц измерения, функций. Имена можно переопределить, но переопределение уничтожит их встроенные значения, и этими константами, единицами измерения и функциями пользоваться будет нельзя.

Оператор локального присваивания для первого раза выберите на математической панели Калькулятор (см. рис. 9.5). Познакомьтесь с содержанием панели. При наведении указателя мыши на какую-либо кнопку появляется всплывающая подсказка с названием оператора, вызываемого щелчком на этой кнопке, и указанием клавиши или сочетания клавиш, нажатие которых вызывает то же действие, что и щелчок на кнопке. В дальнейшем оператор присваивания лучше набирать с клавиатуры, используя клавишу : (двоеточие). Запоминайте клавиши быстрого вызова.

Любой оператор в Mathcad можно ввести тремя способами:

• выбрав команду меню;

• нажав клавишу (сочетание клавиш) на клавиатуре;

• используя математическую панель.

Набрав вычисляемое выражение, нажмите клавишу (равно)  появится численный результат.

Попробуйте набрать  получается . Для правильной записи после набора выражения надо нажать клавишу пробела, чтобы уголок курсора охватил нужную часть выражения. Другой способ  взять выражение в скобки: .

Цепкие операторы

С цепким оператором можно познакомились на примере набора дроби (см. рис. 9.5). Цепкие операторы  это возведение в степень, извлечение корня, деление (ввод знаменателя дроби). Чтобы «вырваться из объятий» цепкого оператора, надо выделить клавишей пробела или клавишей клавиатуры (стрелка вправо) нужную часть выражения, тогда следующий вводимый оператор будет относиться ко всему выделенному выражению.

На первых порах цепкие операторы раздражают. При быстром наборе пользователь обычно забывает о необходимости выделения нужной части выражения. В результате вместо, например, на экране появляется . Поупражняйтесь во введении выражений и получении их результатов.

Для возведения числа в степень используйте символ ^ (он находится на одной клавише с цифрой 6).

Редактирование объектов Mathcad

Редактирование введенных выражений производится обычным для всех Windowsприложений способом.

• Уголок курсора перемещается по экрану с помощью клавиш со стрелками или щелчком левой кнопки мыши в нужном месте экрана.

• Для выделения уголком курсора одного символа надо установить синий уголок курсора так, чтобы он охватывал нужный символ слева или справа.

• Для расширения выделения на часть выражения или все выражение целиком следует использовать клавиши со стрелками или клавишу пробела. Для выхода из цепкого оператора предпочтительно пользоваться клавишей пробела. Уголок курсора должен охватывать все выражение или ту его часть, с которой надо выполнить какие-либо действия.

• Для выделения части выражения или всего выражения надо нажать кнопку мыши в начале или в конце выделяемой части выражения и, не отпуская кнопку мыши, переместить указатель до другого края выделяемого выражения. Можно использовать также сочетание клавиш или . Выделенная часть выражения имеет черный фон. Выделение черным фоном в Mathcad используется для вырезания или копирования части выражения, изменения шрифта, а также для выполнения символьных вычислений с частями выражений.

• Для выделения объекта или группы любых объектов (математических, текстовых или графических) надо нажать кнопку мыши в свободном месте рабочего документа, растянуть пунктирный прямоугольник (рамку выделения) так, чтобы он охватил нужные объекты, и отпустить кнопку мыши. Один объект при этом будет выделен синим уголком курсора, а группа объектов  обведена пунктирной рамкой.

Если надо удалить, вырезать или скопировать в буфер обмена выделенную часть выражения, выделенный объект целиком или группу выделенных объектов, выполните следующие действия:

• для удаления (безвозвратного) объекта нажмите клавишу Delete или Backspace;

• для вырезания объекта в буфер обмена щелкните на кнопке Вырезать Стандартной панели инструментов Mathcad;

• для копирования объекта в буфер обмена щелкните на кнопке Копировать Стандартной панели инструментов Mathcad;

• для вставки объекта из буфера обмена установите крестообразный курсор в то место, куда вы хотите вставить содержимое буфера обмена, и щелкните на кнопке Вставить Стандартной панели инструментов Mathcad.

Поскольку вырезать, копировать, вставлять объекты приходится часто, полезно запомнить сочетания клавиш, нажатие которых вызывает эти действия:

• вырезать  ;

• копировать  ;

• вставить  ;

• отмена предыдущего действия  .

Эти четыре действия выполняются сочетаниями клавиш, расположенных по соседству, и поэтому легко запоминаются.

Как и во всех Windowsприложениях, выделенный объект (группу объектов) можно переместить или скопировать с помощью мыши.

1. Подведите указатель мыши к выделенному объекту или группе объектов, чтобы указатель превратился в изображение черной ладошки.

2. Нажав левую кнопку мыши, перетащите объекты в нужное место, после чего кнопку мыши отпустите. Если выделенные объекты нужно не переместить, а скопировать, при перетаскивании удерживайте клавишу .

Совет

Для вырезания, копирования и вставки объектов удобно использовать команды контекстного меню, которое появляется при щелчке на объекте правой кнопкой мыши.

Встроенные функции

Mathcad содержит свыше 200 встроенных функций. На Стандартной панели инструментов щелкните на кнопке Вставить функцию . В открывшемся диалоговом окне содержится список всех встроенных функций. Просмотрите группы функций (левый список). Щелкнув мышью на любой из групп слева, справа увидите перечень функций, входящих в эту группу.

Ввод встроенных функций покажем на примере групп Логарифм и экспонента и Тригонометрические. Присмотритесь к написанию этих функций (см. листинг рис. 9.5), которое не всегда совпадает с привычной математической записью. Названия функций можно вводить с помощью диалогового окна, появляющегося после щелчка на кнопке Вставить функцию Стандартной панели инструментов. Для этого нужно выделить название функции и щелкнуть на кнопке Добавить в диалоговом окне Вставка функции. Можно также набрать имя функции на клавиатуре в точности так же, как оно записано в диалоговом окне со списком функций.

Наберите и вычислите несколько функций, показанных на рис. 9.6.

Числовые константы и ввод греческих букв

Введенная с клавиатуры латинская буква внутри математического выражения означает основание натурального логарифма . Это значение можно переопределить, присвоив другое значение с помощью знака локального присваивания , например, .

Рис. 9.6. Функции для самостоятельного вычисления

Часто используемое в выражениях число можно ввести с математической панели Калькулятор, где есть кнопка , или с Панели греческих символов, где тоже есть аналогичная кнопка.

Есть и более простой способ ввода греческих букв. Надо на клавиатуре набрать латинский аналог греческой буквы (как правило, это первая буква в латинском названии греческой буквы). Введя аналог греческой буквы, нажмите сочетание клавиш  на экране появится греческая буква (прописная или строчная в зависимости от того, в верхнем или нижнем регистре был набран ее латинский аналог).

Ниже перечислены некоторые греческие буквы и их латинские аналоги:

Наберите несколько выражений с греческими буквами, например: , , и др.

Внимание!

Mathcad вычисляет выражения слева направо и сверху вниз.

Если какой-либо константе или переменной не присвоено никакого значения левее и выше ее положения на экране, то она окрашивается красным цветом, что свидетельствует об ошибке.

Ввод текста

Для ввода текста в документ можно в Главном меню выбрать команду Добавить > Текстовую область, но лучше ввести с клавиатуры символ < " > (двойная кавычка). При этом на экране появляется текстовая область, в которой можно печатать текст.

Еще лучше, сменив латинский шрифт на русский, печатать текст прямо в математической области. Когда напечатано первое слово, при нажатии клавиши пробела область с напечатанным словом автоматически из математической превращается в текстовую.

В текстовую область можно вставлять математическую область, для этого в Главном меню достаточно выбрать команду Добавить > Математическую область. Вставленная математическая область участвует в вычислениях наравне с другими математическими выражениями.

При желании вычисления во вставленной математической области можно запретить. Для этого щелкните правой кнопкой мыши на вставленном выражении и в открывшемся контекстном меню выберите команду Отключить вычисление. После этого вставленное математическое выражение будет играть роль иллюстрации.

Текстовой области в Mathcad по умолчанию назначается стиль Normal (Обычный). Чтобы настроить его, проделайте описанную ниже процедуру.

В Главном меню выберите команду Формат > Стиль. В появившемся диалоговом окне Стили текста выберите нужный в списке Стили.

Функции пользователя

Удобство и эффективность расчетов в Mathcad прежде всего определяются возможностью создания функций пользователя. При многократном вычислении одного и того же выражения без функций пользователя просто не обойтись.

Примеры функций пользователя показаны на рис. 9.7. Слева указывается название функции, а справа после оператора присваивания

Рис. 9.7. Листинг функции пользователя

– вычисляемое выражение. Переменные величины, входящие в правую часть, должны быть записаны в качестве параметров в скобках после имени функции. Все величины из правой части, не входящие в параметры левой части, должны быть заданы численно левее и выше функции пользователя. В противном случае Mathcad указывает на ошибку, окрашивая незаданную величину в красный цвет. При выделении функции щелчком мыши появляется текст сообщения об ошибке Эта переменная не определена.

Функция пользователя не вычисляется Mathcad, а принимается к сведению. Для вычисления функции надо задать численные значения всех параметров в имени функции, набрать имя функции и нажать клавишу (равно) или щелкнуть мышью на кнопке < = > Стандартной панели инструментов или математической панели Калькулятор.

Дискретные (ранжированные) переменные и построение таблиц

Одно из лучших творений создателей Mathcad – это дискретная переменная, играющая роль оператора цикла. (В ряде последних книг по Mathcad ее называют ранжированной переменной, что представляет собой не слишком удачный перевод словосочетания «range variable». Понятие дискретной переменной, характерное для более ранних книг, точнее отражает суть: вместо непрерывной переменной используется ряд чисел, выстроенных в порядке возрастания или убывания).

Без дискретных переменных было бы очень сложно строить графики или таблицы с результатами расчетов. Если в функцию пользователя подставить численное значение переменной, результатом расчета будет число. Дискретная переменная определяет ряд значений, для которых вычисляется функция пользователя, и этот ряд значений функции можно вывести в виде графика или таблицы.

Определение дискретной переменной имеет вид , что означает задание ряда значений .

Пример: , , . В данном случае ответ выводится в виде вектора (рис. 9.8) или графика (рис. 9.9).

С помощью дискретной переменной можно задавать как целые, так и дробные значения переменной, но обязательно равноотстоящие друг от друга. Ниже показаны примеры дискретных переменных.

• – ряд целых чисел от 0 до 5.

• – ряд дробных чисел, где 1 – первое число, 1.1 – второе число, 5 – последнее число. Интервал между числами 1.1–1 =0.1.

• – ряд чисел, где – первое; –второе; – последнее число ( и должны быть заданы заранее), – число интервалов, на которые разбит отрезок от до . Такая форма записи удобна, когда рассматриваются разные варианты одного расчета и изменение констант и позволяет мгновенно пересчитать результаты и перестроить графики.

Внимание!

Знак диапазона (две точки) нельзя набирать с клавиатуры, нажимая два раза клавишу . (точка). Вместо этого надо использовать клавишу ; (точка с запятой) или в математической панели Матрица щелкнуть на кнопке Область переменной .

Если константы, входящие в правую часть функции пользователя, не задаются непосредственно перед вводом функции, Mathcad задействует те значения, которые использовались последними. Проверьте, устраивают ли вас эти значения. Наберите имя параметра и нажмите клавишу < = > (равно).

Рис. 9.8. Числовые результаты для функций листинга рис. 9.7

Построение двухмерного графика функции

Для построения двухмерного графика функции надо выполнить следующую процедуру.

1. Установите крестообразный курсор в то место, где должен быть построен график.

2. На математической панели График щелкните на кнопке Х-У график .

3. В появившемся на месте курсора шаблоне двухмерного графика введите на оси абсцисс имя аргумента – , на оси ординат – имена функций – .

4. Щелкните мышью вне шаблона графика – для заданного диапазона изменения аргумента график будет построен (рис. 9.9).

Рис. 9.9. Графики функций листинга рис. 9.8

Если диапазон значений аргумента не задан, по умолчанию график строится в диапазоне значений аргумента от –10 до 10.

Чтобы в одном шаблоне разместить несколько графиков, следует, набрав на оси ординат имя первой функции, нажать клавишу < , > (запятая) – уголок курсора при этом обязательно должен находиться в конце имени функции, и в появившемся месте ввода (черном квадратике) вписать имя второй функции и т. д.

Если две функции имеют разные аргументы, например и , то на оси ординат надо ввести (через запятую) имена обеих функций, а на оси абсцисс (также через запятую) – имена обоих аргументов и . Тогда первый график будет построен для первой функции по первому аргументу, а второй график – для второй функции по второму аргументу.

Если функций введено несколько, а аргументов два, то график первой функции строится по первому аргументу, а графики остальных функций – по второму аргументу.

Чтобы отформатировать график, дважды щелкните мышью в области графика – откроется диалоговое окно Форматирование выбранного графика X-Y (рис. 9.10).

Рис. 9.10. Вид диалогового окна Форматирование выбранного

Графика X-y

Изучите содержание вкладок окна, задавая различные параметры и щелкая мышью на кнопке Применить или ОК. Смотрите, как изменяется вид графика.

Ниже перечислены вкладки окна форматирования графика.

• Ось X, Первичная ось Y, Вторичная ось Y – форматирование осей координат. Можно нанести линии сетки, показать маркеры, выбрать стиль осей и тип их шкалы. Установите нужные флажки на вкладках.

В Mathcad есть возможность добавления второй оси y, обладающей собственной шкалой (рис. 9.11).

Рис. 9.11. Декартов график с двумя осями координат

Использование двух осей ординат очень удобно, когда на одном и том же графике представляются разнородные данные (например, данные различной размерности, либо различающиеся на несколько порядков, и т. п.).

Для того чтобы задать опцию рисования второй оси ординат:

Откройте вкладку Вторая ось Y и настройте в ней желаемые параметры второй оси, точно так же, как вы это делаете для первой оси.

Нажмите кнопку ОК.

В появившиеся местозаполнители возле второй оси ординат введите желаемые имена переменных или выражения, которые необходимо отложить на данной оси.

• Логарифмическая шкала – график по данной оси будет нарисован в логарифмическом масштабе. Это полезно, если данные разнятся на несколько порядков.

• Линии сетки – показать линии сетки (пример на рис. 9.9).

• Нумерованная – показать нумерацию шкалы. Если убрать этот флажок, то оцифровка шкалы пропадет.

• Автомасштабирование – выбор диапазона оси производится автоматически процессором Mathcad.

• Показать маркеры – выделение значений на осях. Маркером на координатных осях отмечаются метки некоторых важных значений. Маркер представляет собой линию, перпендикулярную оси, снабженную числом или переменной. Чтобы создать маркер установите флажок возле поля Показать маркеры.

При желании выберите цвет маркера, щелкнув на поле справа от флажка.

Нажмите кнопку Применить или ОК.

В появившийся местозаполиитель введите число или имя переменной значение которой вы хотите отобразить на оси маркером (рис. 9.12, слева).

Рис. 9.12. Создание маркеров (слева) и готовые маркеры (справа)

Щелкните вне маркера.

Готовые маркеры показаны на рис. 9.12, справа. На каждой из осей допускается установить по два маркера. Если определен лишь один из них, то второй виден не будет.

• Автосетка – разбиение шкалы производится автоматически процессором Mathcad. Если этот флажок снят, в поле ввода ниже следует указать желаемое количество меток шкалы.

• Равные масштабы – оси х и y принудительно рисуются в одинаковом масштабе.

• Стиль осей – можно выбрать один из трех видов системы координат:

  • Рамка – как показано на рис. 9.9, 9.11.

  • Пересекающиеся – координатные оси в виде двух пересекающихся прямых (рис. 9.13).

  • Нет – координатные оси на графике не показываются.

Рис. 9.13. Координатные оси в виде двух пересекающихся прямых

Изменение диапазона осей

Когда график создается впервые, Mathcad выбирает представленный диапазон для обеих координатных осей автоматически. Чтобы изменить этот диапазон:

1. Перейдите к редактированию графика, щелкнув в его пределах мышью.

2. График будет выделен, а вблизи каждой из осей появятся два поля с числами, обозначающими границы диапазона. Щелкните мышью в области одного из полей, чтобы редактировать соответствующую границу оси (например, верхнего предела оси , как показано нарис. 9.14).

Рис. 9.14. Изменение диапазона оси X

3. Пользуясь клавишами управления курсором и клавишами Васkspace и Del, удалите содержимое поля.

4. Введите новое значение диапазона (например, 20).

5. Щелкните за пределами поля, и график будет автоматически перерисован в новых пределах.

На рис. 9.15 показаны результаты изменения диапазона оси на и оси – на .

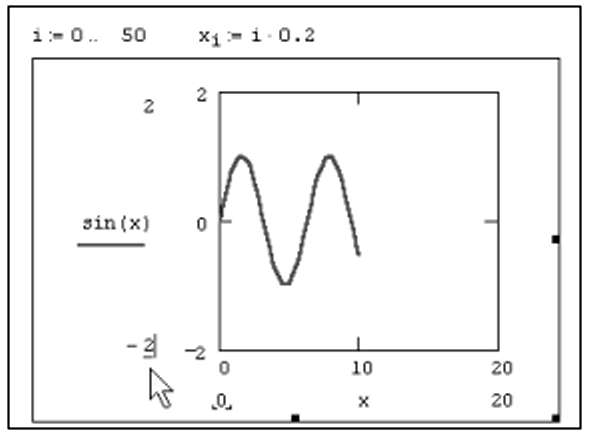
Рис. 9.15. Результат изменения диапазона осей

Чтобы вернуть автоматический выбор какого-либо диапазона, удалите число из соответствующего поля и щелкните вне его. Граница шкалы будет выбрана Mathcad, исходя из значений данных, представляемых на графике.

Форматирование рядов данных

С помощью вкладки Графики диалогового окна Форматирование выбранного графика X-Y (рис. 9.10) легко установить комбинацию параметров линий и точек для каждого из рядов данных, представленных на графике. Пользователю требуется выделить в списке нужный ряд данных (его положение в списке соответствует положению метки зависимости на оси ) и изменить в списках в середине диалогового окна желаемые установки (рис. 9.16).

На вкладке Traces (Ряды данных) регулируются следующие параметры:

• Метка легенды – текст легенды, описывающий ряд данных.

• Символ Частота – частота символов, отмечающих точки (этот параметр определяет будет ли отмечаться каждая точка графика или каждая 2-я, 3-я и т. д.).

• Symbol (Символ) – символ, которым обозначаются отдельные точки данных (рис. 9.17).

Рис. 9.16. Вкладка Графики диалогового окна

Форматирование выбранного графика X-y

• Символ Вес – размер точек данных.

• Линия – стиль линии (рис. 9.18):

• сплошная;

• пунктирная;

• штриховая и т. п.

• Линия Вес – толщина линии.

• Цвет – цвет линии и точек данных.

• Тип – тип представления ряда данных:

• линии;

• точки;

Рис. 9.17. Вкладка Symbol

Рис. 9.18. Вкладка Линия

• ошибка;

• полоса;

• шаг;

• draw – рисунок;

• основа;

• панель заливок.

• Ось Y – информация о том, на какой из двух осей y откладывается ряд данных.

Графики с отложенными ошибками

Тип графика с отложенными ошибками довольно сильно отличается от остальных типов, поскольку требует не двух, а трех серий данных.

Помимо пар декартовых или полярных координат точек необходимо задать еще две последовательности данных, представляющих соответствующие значения ошибок для каждой пары точек (рис. 9.19).

Рис. 9.18. Создание графика с отложенными ошибками

Внимание!

График представления данных с погрешностями требует, чтобы два последовательных ряда данных имели тип графика с ошибками (error).

На рис. 9.19 отложено три ряда данных: (сами данные), (верхняя метка ошибок), (нижняя метка ошибок). Для двух последних рядов в графе Тип уставлен тип ошибка.

Задание

Выполнить расчеты в системе Mathcad в соответствии с рекомендациями, приведенными в листингах настоящей работы.

Практическое занятие №10

Интерполяция и экстраполяция экспериментальных

данных с использованием Mathcad

Цель работы: Научиться интерполировать и экстраполировать экспериментальные данные с использованием Mathcad.

Оборудование, приборы и материалы: ПЭВМ, программа Mathcad 14.

Общие положения

Интерполяция

Если есть выборка экспериментальных данных, то они, чаще всего, представляются в виде массива, состоящего из пар чисел . Поэтому возникает задача аппроксимации дискретной зависимости непрерывной функцией . Функция , в зависимости от специфики задачи, может отвечать различным требованиям:

• должна проходить через точки , т. е. , . В этом случае говорят об интерполяции данных функцией во внутренних точках между или экстраполяции за пределами интервала, содержащего все ;

• должна некоторым образом (например, в виде определенной аналитической зависимости) приближать , не обязательно проходя через точки . Такова постановка задачи регрессии, которую во многих случаях также можно назвать сглаживанием данных;

• должна приближать экспериментальную зависимость , учитывая, к тому же, что данные получены с некоторой погрешностью, выражающей шумовую компоненту измерений. При этом функция , с помощью того или иного алгоритма, уменьшает погрешность, присутствующую в данных . Такого типа задачи называют задачами фильтрации. Сглаживание  частный случай фильтрации.

Различные виды построения аппроксимирующей зависимости иллюстрирует рис. 10.1. На нем исходные данные обозначены кружками, интерполяция  отрезками прямых пунктирных линий, линейная регрессия  наклонной прямой линией, а фильтрация  жирной гладкой кривой.

Рис. 10.1. Разные задачи аппроксимации данных

Для построения интерполяции-экстраполяции в Mathcad имеются несколько встроенных функций, позволяющих "соединить" точки выборки данных кривой разной степени гладкости. По определению, интерполяция означает построение функции , аппроксимирующей зависимость в промежуточных точках между и . Поэтому интерполяцию еще по-другому называют аппроксимацией. В точках значения интерполяционной функции должны совпадать с исходными данными, т. е. .

Линейная интерполяция

Самый простой вид интерполяции  линейная, которая представляет искомую зависимость в виде ломаной линии. Интерполирующая функция состоит из отрезков прямых, соединяющих точки (рис. 10.2).

Для построения линейной интерполяции служит встроенная функция linterp (листинг рис. 10.3).

•  функция, аппроксимирующая данные векторов и кусочно-линейной зависимостью, где:

 вектор действительных данных аргумента;

 вектор действительных данных значений того же размера;

 значение аргумента, при котором вычисляется интерполирующая функция.

Внимание!

Элементы вектора должны быть определены в порядке возрастания, т.е. . Если это не так, следует использовать функцию сортировки .

Рис. 10.2. Линейная интерполяция (листинг рис. 10.3)

Рис. 10.3. Листинг линейная интерполяция

Сплайн-интерполяция

В большинстве практических приложений желательно соединить экспериментальные точки не ломаной линией, а гладкой кривой. Лучше всего для этих целей подходит интерполяция сплайнами, т. е. отрезками полиномов (чаще всего кубических парабол, как это показано на рис. 10.4).

Рис. 10.4. Кубическая сплайн- интерполяция (листинг рис. 10.5)

•  функция, аппроксимирующая данные векторов и кубическими сплайнами, где:

  •  вектор вторых производных, созданный одной из сопутствующих функций . или ;

  •  вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;

  •  вектор действительных данных значений того же размера;

  •  значение аргумента, при котором вычисляется интерполирующая функция.

Сплайн-интерполяция в Mathcad реализована чуть сложнее линейной. Перед применением функции необходимо предварительно определить первый из ее аргументов  векторную переменную . Делается это при помощи одной из трех встроенных функций тех же аргументов :

•  вектор значений коэффициентов линейного сплайна;

•  вектор значений коэффициентов квадратичного сплайна;

•  вектор значений коэффициентов кубического сплайна где:

  •  векторы данных.

Выбор конкретной функции сплайновых коэффициентов влияет на интерполяцию вблизи конечных точек интервала. Пример сплайн-интерполяции приведен в листинге рис. 10.5.

Рис. 10.5. Листинг кубическая сплайн- интерполяция

Более сложный тип интерполяции  так называемая интерполяция В-сплайнами. В отличие от обычной сплайн-интерполяции, сшивка элементарных В-сплайнов производится не в точках , а в других точках  , координаты которых предлагается ввести пользователю. Сплайны могут быть полинома­ми 1, 2 или 3 степени (линейные, квадратичные или кубические). Применяется интерполяция В-сплайнами точно так же, как и обычная сплайн-интерполяция, различие состоит только в определении вспомогательной функции коэффициентов сплайна (листинг рис 10.6):

•  вектор значений коэффициентов В-сплайна, где:

  •  векторы данных аргумента и значений;

  •  вектор значений аргумента, в которых производится сшивка В- сплайнов;

  •  порядок полиномов сплайновой интерполяции (1, 2 или 3).

Рис. 10.6. Листинг интерполяция В-сплайнами

Примечание

Размер вектора должен быть на 1, 2 или 3 меньше размера векторов и . Первый элемент вектора должен быть меньше или равен первому элементу вектора (т. е. лежать за пределами левой границы интервала интерполирования). Последний элемент должен быть больше или равен последнему элементу (т. е. находиться за правой границей интервала интерполирования).

Экстраполяция функцией предсказания

. В Mathcad имеется инструмент экстраполяции, который учитывает распределение данных вдоль всего интервала. В функцию встроен линейный алгоритм предсказания поведения функции, основанный на анализе, в том числе осцилляций.

•  функция предсказания вектора, экстраполирующего выборку данных, где:

  •  вектор действительных значений, взятых через равные промежутки значений аргумента;

  •  количество последовательных элементов вектора , согласно которым строится экстраполяция;

  •  количество элементов вектора предсказаний.

Пример использования функции предсказания на примере экстраполяции осциллирующих данных с меняющейся амплитудой приведен в листинге рис. 10.7. Полученный график экстраполяции, наряду с самой функцией, показан на рис. 10.8. Аргументы и принцип действия функции отличаются от рассмотренных выше встроенных функций интерполяции / экстраполяции. Значений аргумента для данных не требуется, поскольку по определению функция действует на данные, идущие друг за другом с равномерным шагом. Обратите внимание, что результат функции вставляется "в хвост" исходных данных.

Рис. 10.7. Листинг экстраполяция при помощи функции предсказания

Рис. 10.8. Экстраполяция при помощи функции предсказания

(листинг рис. 10.7)

Как видно из рис. 10.8, функция предсказания может быть полезна при экстраполяции данных на небольшие расстояния. Вдали от исходных данных результат часто бывает неудовлетворительным. Кроме того, функция хорошо работает в задачах анализа подробных данных с четко прослеживающейся закономерностью (типа рис. 10.8), в основном осциллирующего характера. Однако если данных мало, результат работы функции предсказания может оказаться неудовлетворительным.

Задание

Для приведенной в [1] выборки экспериментальных значений параметров, определяющих зависимость между переменными x и y (в соответствии с индивидуальным вариантом), используя Mathcad, необходимо реализовать интерполяцию и экстраполяцию данных.

Практическое занятие №11

Построение регрессии и сглаживание экспериментальных

данных с использованием Mathcad

Цель работы: Научиться строить регрессию и сглаживать экспериментальные данные с использованием Mathcad.

Оборудование, приборы и материалы: ПЭВМ, программа Mathcad 14.

Общие положения

Регрессия

Задачи математической регрессии имеют смысл приближения выборки данных некоторой функцией , определенным образом минимизирующей совокупность ошибок . Регрессия сводится к подбору неизвестных коэффициентов, определяющих аналитическую зависимость . В силу производимого действия большинство задач регрессии являются частным случаем более общей проблемы сглаживания данных.

Как правило, регрессия очень эффективна, когда заранее известен (или, по крайней мере, хорошо угадывается) закон распределения данных .

Линейная регрессия

Самый простой и наиболее часто используемый вид регрессии  линейная. Приближение данных осуществляется линейной функцией . На координатной плоскости линейная функция, как известно, представляется прямой линией (рис. 11.1).

Рис. 11.1. Линейная регрессия (листинги рис. 11.2 или 11.3)

Еще линейную регрессию часто называют методом наименьших квадратов, поскольку коэффициенты и вычисляются из условия минимизации суммы квадратов ошибок .

Примечание

Чаще всего такое же условие ставится и в других задачах регрессии, т. е. приближения массива данных другими зависимостями . Исключение рассмотрено в листинге 10.7.

Для расчета линейной регрессии в Mathcad имеются два дублирующих друг друга способа. Правила их применения представлены в листингах 11.2 и 11.3. Результат обоих листингов получается одинаковым (рис. 11.1).

•  вектор из двух элементов коэффициентов линейной регрессии ;

•  коэффициент линейной регрессии;

•  коэффициент линейной регрессии, где:

  •  вектор действительных данных аргумента;

  •  вектор действительных данных значений того же раз мера.

Рис. 11.2. Листинг линейная регрессия

Рис. 11.3. Другая форма записи листинга линейная регрессия

Кроме того, в Mathcad имеется альтернативный алгоритм, реализующий не минимизацию суммы квадратов ошибок, а медиан-медианную линейную регрессию для расчета коэффициентов и .

•  вектор из двух элементов коэффициентов линейной медиан-медианной регрессии , где:

  •  векторы действительных данных одинакового размера.

Полиномиальная регрессия

В Mathcad реализована регрессия одним полиномом, отрезками нескольких полиномов, а также двумерная регрессия массива данных, причем она осуществляется в комбинации со встроенной функцией полиномиальной интерполяции:

•  вектор коэффициентов для построения полиномиальной регрессии данных;

•  вектор коэффициентов для построения регрессии данных фрагментами полиномов;

•  результат полиномиальной регрессии, где:

  • ;

  •  вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;

  •  вектор действительных данных значений того же размера;

  •  степень полинома регрессии (целое положительное число);

  •  положительный параметр сглаженности данных, определяющий размер фрагментов полиномов (хорошие результаты дает значение );

  • t  значение аргумента полинома регрессии.

Внимание!

Для построения регрессии полиномом к-ой степени необходимо наличие, по крайней мере, (k+l) точек данных, а для построения полиномиальной регрессии после функции необходимо использовать функцию .

Пример полиномиальной регрессии квадратичной параболой приведен в листинге рис. 11.4, а ее результат показан на рис. 11.5.

Рис. 11.4. Листинг полиноминальная регрессия

Рис. 11.5. Регрессия полиномами разной степени

(листинг 11.4 для разных )

Сглаживание

Помимо регрессии, в Mathcad имеется несколько встроенных функций, реализующих различные алгоритмы сглаживания данных:

•  сглаживание алгоритмом "бегущих медиан";

•  сглаживание на основе функции Гаусса;

•  локальное сглаживание адаптивным алгоритмом, основанное на анализе ближайших соседей каждой пары данных, где:

  •  вектор действительных данных аргумента (для его элементы должны быть расположены в порядке возрастания);

  •  вектор действительных значений того же размера, что и ;

  •  ширина окна сглаживания.

Все функции имеют в качестве аргументов векторы, составленные из массива данных, и выдают в качестве результата вектор сглаженных данных того же размера. Функция предполагает, что данные расположены равномерно.

Примеры сглаживания при помощи "бегущих медиан" и функции Гаусса с разным значением ширины окна пропускания показаны на рис. 11.6 и 11.7 соответственно.

Рис. 11.6. Сглаживание "бегущими медианами"

Рис. 11.7. Сглаживание при помощи функции

Задание

Для приведенной в [1] выборки экспериментальных значений параметров, определяющих зависимость между переменными x и y (в соответствии с индивидуальным вариантом), используя Mathcad, необходимо реализовать регрессию и сглаживание данных.

Литература

1. Методические указания к выполнению индивидуального задания по дисциплине «Компьютерное проектирование в сварочном производстве» (для студентов специальностей "Технология и оборудование сварки" и " Восстановление и повышенияе износостойкости деталей машин и конструкций ") /Сост. В.А. Шевченко, А.В. Каленская. - Луганск: Изд-во Восточноукр. нац. ун-та им. В. Даля, 2011. - 7с.

Учебное издание

Методические указания

к практическим занятиям

по дисциплине «Компьютерное проектирование

в сварочном производстве»

(для студентов, обучающихся по направлению

подготовки – 6.050504 “Сварка”)

Составители

Владимир Алексеевич ШЕВЧЕНКО

Андрей Борисович ЖИДКОВ

Анна Васильевна КАЛЕНСКАЯ

Редактор И. И. Иванова

Техн. редактор С. К. Николаева

Оригинал-макет В. В. Сидоров

Подписано в печать ________

Формат 60×84¹/₁₆ Бумага типограф. Гарнитура Times.

Печать офсетная. Усл. печ. л.______. Уч.-изд. л. ______.

Тираж ____ экз. Изд. № ______. Заказ № _______. Цена договорная.

Издательство Восточноукраинского национального университета имени Владимира Даля

Адрес издательства : 91034, г. Луганск, кв. Молодежный, 20а

Телефон: 8 (0642) 41-34-12, факс. 8 (0642) 41-31-60

E-mail: uni@snu.edu.ua http: www.snu.edu.ua

115