53) Осмотическое давление коллоидных растворов. Уравнение Вант – Гоффа. Значение явление осмоса в коллоидных системах.

В истинных растворах, отделенных от растворителя полупроницаемой перегородкой, может быть измерено осмотическое давление, величина которого зависит от концентрации растворенного вещества и для разбавленных растворов описывается уравнением Вант Гоффа

, (2.2.96)

где С – массовая концентрация, кг/м3.

Для коллоидных систем можем записать

, (2.2.97)

где n – частичная концентрация частиц/м3.

Из уравнения (2.2.97) следует, что осмотическое давление пропорционально частичной концентрации. Число частиц в коллоидной системе очень мало по сравнению с истинным раствором, поэтому осмотическое давление золей тоже очень мало. Например,1%-ный золь золота с частичками r» 10-9м имеет осмотическое давление p = 3,45 Па. Чтобы этот золь имел такое же осмотическое давление, как 1М-раствор электролита, понадобилось бы в 1 дм3 диспергировать 50 кг золота с частичками r = 10-9 м.

Очевидно, что при малом осмотическом давлении золя даже малейшая примесь электролита будет оказывать колоссальное влияние на осмотическое давление, поэтому при изучении осмоса в золях их требуется тщательно очищать.

Осмос - спонтанный переход, односторонняя диффузия через полупроницаемую перегородку ( мембрану ), отделяющую раствор от чистого растворителя или раствора меньшей концентрации. Обусловлен стремлением системы к термодинамическому равновесию и выравниванию концентраций р с обеих сторон мембраны.Характеризуется осмотическим давлением, равным избыточному внешнему давлению, которое нужно приложить со стороны раствора, чтобы прекратить осмос. Играет важную роль в физиологических процессах, используется при исследовании, биологических структур.

54). Задачи и методы сидиментационного анализа.

седиментация (англ. sedimentation) — (от лат. sedimentum — оседание) — оседание частиц дисперсной фазы (твердых крупинок, капелек жидкости, пузырьков газа) в жидкой или газообразной дисперсионной среде в гравитационном поле или в поле центробежных сил.

Описание

Седиментация происходит, если направленное движение частиц под действием силы тяжести или центробежной силы преобладает над хаотическим тепловым движением частиц. Скорость седиментации зависит от массы, размера и формы частиц, вязкости и плотности среды, а также ускорения, возникающего при действии на частицы упомянутых выше сил. Седиментация в дисперсных системах (особенно с газовой дисперсионной средой) часто сопровождается укрупнением седиментирующих частиц вследствие коагуляции или коалесценции. Седиментация в центрифугах и ультрацентрифугах, а также в гравитационном поле лежит в основе седиментационного анализа.

Частицы дисперсной фазы в гравитационном поле оседают, если их плотность больше плотности дисперсионной среды, или всплывают, если их плотность меньше плотности дисперсионной среды. Следствием процесса седиментации является возникновение градиента концентраций частиц по высоте сосуда, приводящего к диффузии, направленного в сторону меньшей концентрации. Сравнение седиментационного (iсед) и диффузионного (iдиф) потоков позволяет установить, какой из процессов преобладает в данной дисперсной системе. Для нахождения закона распределения частиц по высоте исходят из равенства потоков диффузии и седиментации (iсед = iдиф), т.е. из условия седиментационно – диффузионного равновесия. Поток седиментации рассчитывают по уравнению (1)  где uсед - линейная скорость седиментации; п - число частиц в единице объема (частичная концентрация). Условием равномерного движения частицы является равенство силы тяжести и силы трения; последняя для сферической частицы радиуса r определяется по уравнению Стокса; (2)  Скорость седиментации с учетом поправки на потерю в массе по закону Архимеда выразится уравнением (3)  где т—масса частицы; g - ускорение свободного падения; ρ и ρ0 - плотность дисперсной фазы и дисперсионной среды. Диффузионный поток рассчитывают по уравнению Фика: (4)  Здесь   - градиент концентрации по высоте H. Приравняв правые части уравнений (4) и (5), получают выражение седиментационно - диффузионного равновесия, называемое уравнением Лапласа—Перрена: (5)  где п и п0 - число частиц на исходном уровне и на высоте H соответственно. Уравнение (5) является частным случаем универсального закона распределения Больцмана:  (6)

где U— потенциальная энергия; для гравитационного поля с учетом поправки по закону Архимеда:  (7) Уравнение (5) было получено раньше независимо от закона Больцмана. Определение размеров частиц может быть проведено двумя методами: по измерению скорости седиментации и на основании исследования распределения частиц по высоте. Первый метод широко используется для грубодисперсных систем с размерами частиц более 10-6м. На этом методе основан седиментационный анализ грубодисперсных систем. Второй метод определения размеров частиц - по седиментационно-диффузионному равновесию - непригоден для грубодисперсных систем (там практически отсутствует поступательное броуновское движение). Для коллоидных систем (размеры частиц 10-7 – 10-9м) этот метод в гравитационном поле практически не используется, так как здесь существенно преобладает тепловое движение частиц над седиментацией. Расчет показывает, что частицы размером 10-7—10-9 м удерживаются тепловым движением во взвешенном состоянии. Их концентрация во всем объеме остается практически постоянной - такие системы седиментационно устойчивы. Метод определения размеров частиц по седиментационно-диффузионному равновесию успешно используется с применением центробежного поля, при этом регулирование скорости вращения центрифуги позволяет применять этот метод в достаточно большом интервале размеров. Используя ультрацентрифугу, можно определять также молекулярную массу полимеров.

55) Коллоидные системы, так же как и истинные растворы, поглощают, отражают и преломляют свет. Их отличительной особенностью является способность рассеивать свет (явление опалесценции). Опалесценция становится особенно заметной, если через коллоидный раствор пропускать пучок сходящихся лучей, поставив между источником света и кюветой с раствором линзу. В этих условиях в коллоидном растворе, наблюдаемом сбоку, виден ярко светящийся конус (конус Тиндаля). Рассеивание света наблюдается только тогда, когда длина световой волны (λ) больше размера частицы дисперсной фазы. Если λ меньше диаметра частиц, наблюдается отражение света.  Рэлей вывел уравнение, связывающее интенсивность опалесценции с размером частиц и концентрацией частиц в системе: 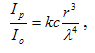уравнение Рэлея где I0 – интенсивность падающего света, Ip – интенсивность опалесценции, Ip/I0 – мутность системы, k –константа, с –концентрация (кг/м3), r – радиус частицы (м), λ –длина волны падающего света (м). Уравнение выведено при следующих допущениях: 1) частицы имеют сферическую форму и не проводят электрический ток; 2) размер частиц не должен быть более 1/10 от λ (40-50 мкм); при увеличении размера частиц показатель степени λ уменьшается; при очень больших размерах показатель степени превращается в нуль и светорассеивание переходит в отражение света; 3) большое расстояние между частицами (разбавленная система). При больших концентрациях возникает многократное рассеивание и прямая зависимость между Ip/I0 и концентрацией нарушается. Выводы из уравнения Рэлея: 1. При уменьшении размера частиц опалесценция резко уменьшается (в 3-ей степени), поэтому при облучении истинных растворов опалесценция не наблюдается. Однако она будет наблюдаться, если для облучения будут использованы излучения с малой длиной волны (например, рентгеновское). 2. Для частиц данного размера мутность Ip/I0 прямо пропорциональна концентрации частиц коллоидной системы. Это позволяет определять концентрацию по мутности раствора. 3. При облучении бесцветных коллоидных систем белым светом рассеиваются главным образом короткие волны (синие), т.к. Ip обратно пропорционально λ4. Поэтому при боковом освещении бесцветные коллоидные системы имеют синеватую окраску, а в проходящем свете – красноватую (дополнительный к синему цвет).  4. Коэффициент k в уравнении Рэлея зависит от соотношения величин показателей преломления дисперсной фазы и дисперсионной среды. Если они одинаковы, то k ≈ 0, светорассеивания нет.

ТИНДАЛЯ ЭФФЕКТ -свечение оптически неоднородной среды вследствие рассеяния проходящего через неё света. Обусловлен дифракцией света на отд. частицах или элементах структурной неоднородности среды, размер к-рых намного меньше длины волны рассеиваемого света. Характерен для коллоидных систем (напр., гидрозолей, табачного дыма) с низкой концентрацией частиц дисперсной фазы, имеющих показатель преломления, отличный от показателя преломления дисперсионной среды. Обычно наблюдается в виде светлого конуса на тёмном фоне (конус Тиндаля) при пропускании сфокусированного светового пучка сбоку через стеклянную кювету с плоскопараллельными стенками, заполненную коллоидным раствором. Коротковолновая составляющая белого (немонохроматического) света рассеивается коллоидными частицами сильнее длинноволновой, поэтому образованный им конус Тиндаля в непоглощающем золе имеет голубой оттенок.

T. э. по существу то же, что опалесценция. Но традиционно первый термин относят к интенсивному рассеянию света в ограниченном пространстве по ходу падающего луча, а второй-к слабому рассеянию света всем объёмом наблюдаемого объекта.

T. э. воспринимается невооружённым глазом как равномерное и непрерывное свечение нек-рой части объёма рассеивающей свет системы. На самом деле свет исходит от отд. точек-дифракционных пятен, хорошо различимых под оптич. микроскопом при достаточно сильном освещении разбавленного золя. Интенсивность рассеянного в данном направлении света (при пост. параметрах падающего света) зависит от числа рассеивающих частиц и их размера.

Основанные на T. э. оптич. методы обнаружения, определения размера и концентрации коллоидных частиц [ультрамикроскопия (см. Ультрамикроскоп), нефелометрия] широко применяются в науч. исследованиях и промышл. практике.

56) Абсорбция света. Закон Бугера – Ламберта – Бэра. Мутность, светопропускание, оптическая плотность раствора. Методы нефелометрии и турбидеметрии, ультрамикроскопии, их практическое применение.

когда свет проходит через какое-нибудь материальное тело, он в большей или меньшей степени задерживается им. Закон поглощения света, известный как закон Ламберта-Бугера-Беера, имеет вид

, (2.2.109)

где I– интенсивность прошедшего света, I0– интенсивность падающего света, exp – основание натурального логарифма, e– постоянная абсорбции – постоянная, характеризующая поглощающую способность данного тела, l – длина поглощающего слоя.

При прохождении света через раздробленную систему, поглощение его происходит как дисперсионной средой, так и диспергированными частицами. Если дисперсионная среда для данного света с определенной длиной волны является прозрачной, это означает, что в системе имеется только один поглотитель – раздробленноевещество. В этом случае закон поглощения света будет иметь вид

, (2.2.110)

где с– концентрация раздробленного вещества; Е – постоянная абсорбции, отнесенная к выбранной единицеконцентрации.

Если и диспергированное вещество не поглощает света, то Е = 0 и I = I0, тогда в дисперсной системе будет проявляться только светорассеяние. Очевидно, что для коллоидных систем закон поглощения света должен быть гораздо сложнее. Прежде всего, как и в случае опалесценции, необходимо различать системы с непроводящими и с проводящими частицами. Системы с непроводящими частицами по характеру своейабсорбции света наиболее близко подходят к истинным растворам. Однако в этих системах часто наблюдаются отклонения от закона поглощения света. Эти отклонения могут быть следствием изменения степени дисперсности раздробленной фазы. Для этих систем поглощение света можно описать уравнением

, (2.2.111)

где А– коэффициент фиктивной абсорбции.

Если частички бесцветны (белые золи), то Е = 0, и следовательно происходит не абсорбция света, а его рассеяние, постоянная А является функцией длины волны l. Установлено, что коэффициент фиктивнойабсорбции обратно пропорционален la, где показатель степени при длине волны а зависит от степенидисперсности частиц в системе.

Зако́н Бугера — Ламберта — Бера — физический закон, определяющий ослабление параллельного монохроматического пучка света при распространении его в поглощающей среде.

Закон выражается следующей формулой:

,

где I0 — интенсивность входящего пучка, l — толщина слоя вещества, через которое проходит свет, kλ — показатель поглощения (часто неправильно именуется коэффициентом поглощения).

Показатель поглощения характеризует свойства вещества и зависит от длины волны λ поглощаемого света. Эта зависимость называется спектром поглощения вещества. Для растворов поглощающих веществ в непоглощающих растворителях показатель поглощения может быть записан как

,

где   — коэффициент, характеризующий взаимодействие молекулы поглощающего вещества со светом длины волны λ, C — концентрация растворённого вещества. Утверждение, что χλ не зависит от C, называется законом Бера (не путать с законом Бэра). Его смысл состоит в том, что способность молекулы поглощать свет не зависит от состояния других окружающих молекул. Однако наблюдаются многочисленные отклонения от этого закона, особенно в случае больших концентраций C.

молекулярной структуры, степени кристаллизации либо посторонних включений на поверхности или внутри образца полимера. Мутность свойственна только полупрозрачным или прозрачным материалам и не относится к непрозрачным материалам. Мутность иногда считают противоположностью к глянцу, который собственно может быть поглощением падающего пучка света. Однако согласно методу испытания на мутность, фактически измеряют поглощение, пропускание и отклонение луча света полупрозрачным материалом. Образец помещают на пути узкого пучка света таким образом, что часть света проходит через образец, а другая часть не встречает препятствия. Обе части пучка проходят в сферу, оснащенную фотодетектором. Можно определить две величины: Общую интенсивность пучка света; Количество света, отклоненного более чем на 2,5° от исходного пучка. По этим двум величинам можно вычислить следующие два значения: Мутности, или процента подающего света, рассеянного более чем на 2,5°, Коэффициента светопропускания, или процента падающего света, который пропускается через образец. 

оптическая плотность.

Определяемая уровнем поглощения света количественная характристика раствора, которая, в соответствии с законом Бира-Ламберта, прямо пропорциональна концентрации растворенного вещества, - E=lgIo/I=kcb (где Io - интенсивность поглощенного света, I - то же прошедшего, k - толщина слоя раствора, c - молярная концентрация); на основе определения параметров О.п.построен фотометрический количественный анализ

В нефелометрии измеряется интенсивность света, рассеянного дисперсной системой. Вместо измерения абсолютных значений рассеянного света на практике проводят сравнение интенсивностей лучей, рассеянных стандартным и исследуемым золем. На рис. 2,а приведена схема визуального нефелометра Кляйнмана (нефелометры иногда называют тиндалеметрами). При измерении подниманием или опусканием экранов изменяют высоту осветленной части пробирок с золями, добиваясь одинаковой осветленности в обеих половинах окуляра. При подчинении исследуемой монодисперсной системы уравнению Рэлея для интенсивности рассеянного света можно записать

Р = /о[^^2 (1+со529)] (IV. 1)  где /о — интенсивность падающего света; ,Р — функция показателей преломления; V — концентрация частиц в единице объема системы; V — объем частицы; X — длина волны падающего света; Л — расстояние частицы от источника света; 9 — угол между направлениями распространения рассеянного света и падающего света. 

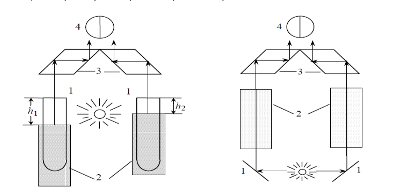
Рис.2 Схема нефелометра -а Схема турбидиметра - б

а - 1 – зеркала, 2 – кюветы, 3 – призмы, 4 – окуляр.

б - 1 – пробирки с золями, 2 - экраны, 3 –призмы, 4 – окуляр

В турбидиметрии измеряют интенсивность света, прошедшего через стандартную и исследуемую дисперсную систему. Схема визуального турбидиметра приведена на рис. 2,б. Оптическая плотность раствора пропорциональна концентрации и объему частиц дисперсной фазы

D = k′cV .

При одинаковой осветленности поля зрения в окуляре имеем равенство cстандVстанд = cхVх, применение, которого аналогично рассмотренному для нефелометрии.