TAY 48

1. Застосувавши правила структурних перетворень визначити функції передачі САУ відносно задаючого впливу g(t) (в тому числі по похибці) і відносно збурення f(t), скориставшись структурною схемою системи.

Функція передачі розімкнутої системи:

Функція передачі відносно задаючого впливу :

;

Функція передачі відносно збурення :

;

Функція передачі відносно похибки:

2. Застосувавши правила структурних перетворень визначити функції передачі САУ відносно задаючого впливу g(t) (в тому числі по похибці) і відносно збурення f(t), скориставшись структурною схемою системи.

Об”єднуємо блоки W1 i W2: , а також блоки W3 і W02:

Переносимо блок W4 через суматор, одержуємо наступну схему:

, переносимо блок 8 через суматор за ходом сигналів.

Об”єднуємо блоки W13 i W4 : , а також W14 I W10

одержуємо спрощену структурну схему:

Функція передачі розумкнутої системи:

Функція передачі відносно задаючого впливу :

;

Функція передачі відносно збурення :

;

Функція передачі відносно похибки:

3. Знайти оригінал, який відповідає зображенню функції Y(s). Провести перевірку розрахунків, застосувавши перетворення за Лапласом отриманого оригіналу у(t). Зображення функції y(t) задане наступним виразом:

Р озкладаємо зображення на прості дроби:

Зводимо до спільного знаменника і розглядаємо тільки чисельники:

Складаємо систему рівнянь, прирівнюючи коефіцієнти при рівних степенях.

А2+В=0

Знаходимо

Тобто, за таблицями маємо

Знаходимо оригінал:

п роводимо перевірку:

Отже, перетворення проведено правильно.

4. Знайти оригінал, який відповідає зображенню функції Y(s). Провести перевірку розрахунків, застосувавши перетворення за Лапласом отриманого оригіналу y(t). Зображення функції Y(s) задане наступним, виразом:

Розкладаємо зображення на прості дроби:

Зводимо до спільного знаменника і розглядаємо тільки чисельники:

Складаємо систему рівнянь, прирівнюючи коефіцієнти при рівних степенях.

Знаходимо

Тобто, за таблицями маємо

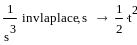
Знаходимо оригінал:

проводимо перевірку:

Отже, перетворення проведено правильно.

5.Знайти орігінал, який відповідає зображенню функції Y(s). Провести перевірку розрахунків, застосувавши перетворення за Лапласом отриманого орігіналу y(t). Зображення функції Y(s) задане наступним виразом:

Розкладаємо зображення на прості дроби:

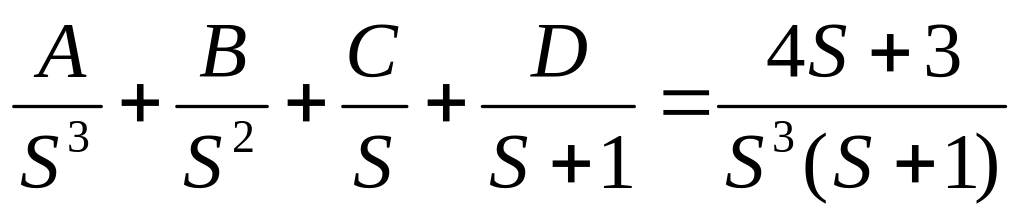
Зводимо до спільного знаменника і розглядаємо тільки чисельники:

Складаємо систему рівнянь, прирівнюючи коефіцієнти при рівних степенях.

Тобто, за таблицями маємо

Знаходимо оригінал:

проводимо перевірку:

Отже, перетворення проведено правильно.

6. Побудувати АФЧХ розімкнутої системи, якщо її функція передачі має наступний вираз:

.

де k=2; ,1 с; а₂=0,8 с²; а₁=1 с.

На основі побудованої АФЧХ вірішити питання про стійкість системи в замкнутому стані.

З перехідного процесу видно, що розімкнута система є стійкою. Оскільки АФЧХ розімкнутої системи охоплює точку (-1;j0). То замкнута система є не стійкою (згідно критерію Найквіста).

7. Побудувати логарифмічні частотні характеристики інтегро-диференційного элемента САУ за наступною функцією передачі:

.

Дана функція передачі є послідовним з’єднанням форсуючої ланки, інтегратора та аперіодичної ланки першого порядку

Шукаємо частоти перегину графіка

ЛАЧХ: - логарифмічна амплітудо-частотна характеристика

ЛФЧХ:-логарифмічна фазо-частотна характеристика

w=0:0.1:10;

s=j*w;

P=(s+10)./(0.01.*s.^2+s);

W=tf([1 10],[0.01 1 0])

bode(W);grid

8. Одноконтурна сау складається з коливної і інтегруючої ланки . З’ясувати, при якому значенні коефіцієнта передачі розімкнутої системи вона залишається стійкою.

де k - передаточний коефіцієнт; Т₁=0,01 - постійна часу ланок; ξ₁=0,1 - коефіцієнт демпфування коливних ланок.

Замкнемо систему і запишемо рівняння знаменника, тобто

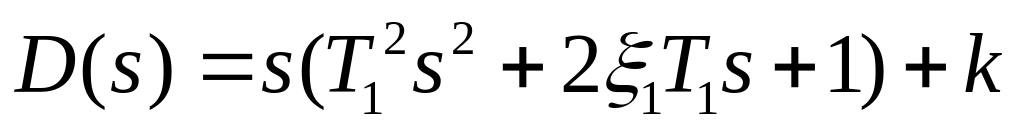,так як Т₁²=(0,01)², 2ξ₁Т₁=2*10^-3.

D(s)=10^-4*s³+2*10^-3s²+s+k, отже D(s)=a3s³+a2s²+a1s+a0

Використовується критерій стійкості Гурвіца. З коренів характеристичного рівняння складають матрицю. Критерій формулюється так: щоб система була стійкою, необхідно і достатньо при а0>0 мати додатніми всі діагональні визначники матриці.

в іншій формі

Для стійкості системи четвертого порядку треба щоб всі коефіцієнти були >0 і виконувалась рівність

В іншій формі визначник d=k(2*10^-3-10^-4k).Прирівняємо визначник до 0 і визначимо k.

K=2*10^-3/10^-4=2*10=20.

Отже при такому к система буде стійка.

9. Дослідити на стійкість сар, розімкнутий ланцюг якої має наступну функцію пердачі:

де k=2; ,2 с; T₁=0,05 c; T₂=1 c.

де

k=3; tau=0.2;

T1=0.5; T2=1;

w=0.01:0.01:10;

w1=tf([tau 1],[T1 0 1])

w2=tf([1],[T2 1])

w3=w1*w2^2*k;

w4 = feedback(w3,1);

step(w4),grid;

Система є нестійкою.

10. Дослідити САУ на стійкість за допомогою логарифмічних частотних характеристик та визначити чи володіє досліджувана система запасами стійкості по фазі та амплітуді. Задана передатна функція САУ в наступному вигляді:

де k=3; Т₁=0,2 с; τ_=1 с; τ₂=0,1 с.

w=0:0.1:10;

s=j*w;

w1=tf([0 3],[1 0])

w2=tf([1 1],[1 0])

w3=tf([1 1],[0.2 1])

w=w1*w2*w3

margin(w);grid

Система являється стійкою оскільки не існує точки в якій система перетинає -180 градусів.

11. Визначити граничне значення коефіцієнта підсилення розімкнутої САУ з наступною функцією пердачі:

де T₁=1 c; T₁=0,2 c та =0,4.

Використовується критерій стійкості Гурвіца. З коренів характеристичного рівняння складають матрицю. Критерій формулюється так: щоб система була стійкою, необхідно і достатньо при а0>0 мати додатніми всі діагональні визначники матриці.

Для стійкості системи третього порядку треба щоб всі коефіцієнти були >0 і виконувалась рівність

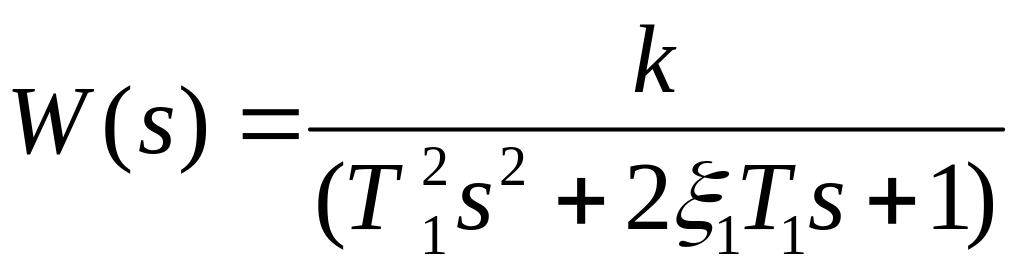
Після перетворення одержимо

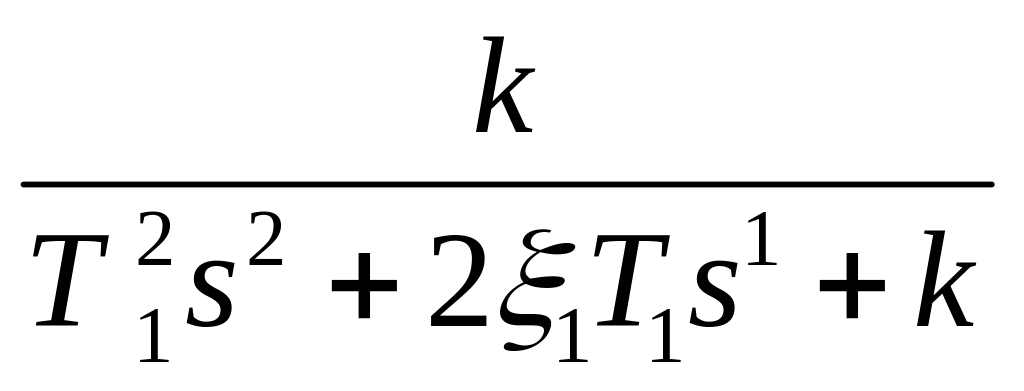
Запишемо характеристичне рівняння замкнутої системи

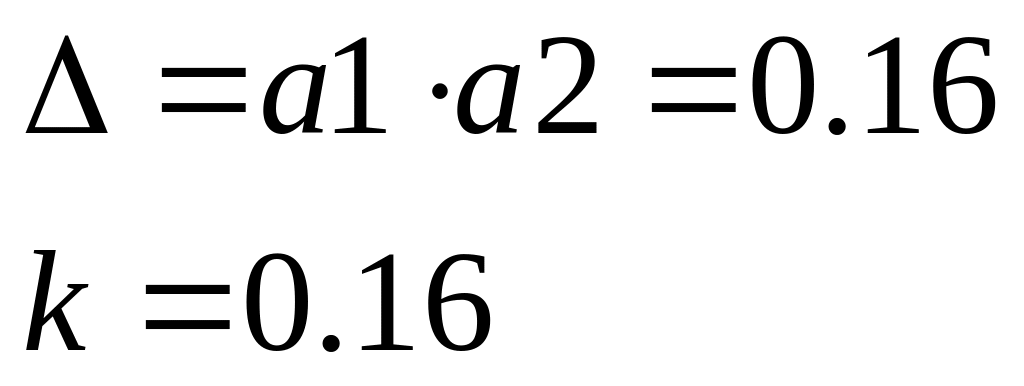Для границі стійкості повинна виконуватись умова

12 Функція розімкнутої САУ має наступний вигляд:

де

З’ясувати вплив постійної часу диференцюючої ланки на стійкість замкнутої системи.

k=2; tau=0.001;

T1=4; T2=2;

w=0.01:0.01:10;

w1=tf([tau 1],[T1 0 1])

w2=tf([1],[T2 1])

w3=w1*w2*k;

w4 = feedback(w3,1);

s tep(w4),grid,title('При tau=0.001');

З графіків видно, що при збільшенні постійної часу тау, коливні процеси збільшуються

13. Функція передачі розімкнутої САУ має наступний вигляд:

де k=5; T₁=0,4 c.

З’ясувати вплив постійної часу _ диференцюючої ланки та постійної часу T₂ на стійкість замкнутої системи.

k=5; tau=0.001;

T1=0.4;

w=0.01:0.01:10;

w1=tf([tau 1],[T1 1])

w2=tf([5],[1 0])

w3=w1*w2*k;

w4 = feedback(w3,1);

step(w4),grid,title('При tau=0.001');

Та при tau=0.1

При збільшені tau система стає стійкою

14. З’ясувати вплив на стійкість САУ коефіцієнта передачі k її розімкнутого ланцюга. Функція передачі САУ має наступний вигляд:

де T₁=0,4 c; =1 c.

k=2; tau=1;

T1=0.4;

w=0.01:0.01:10;

w1=tf([tau 1],[T1 1])

w2=tf([k],[1 0])

w3=w1*w2*k;

w4 = feedback(w3,1);

step(w4),grid,title('При k=2');

та графік при k=20

15. Функції передачі окремих участків САУ має наступний вигляд:

Розрахувати стале значення похибки, якщо задаюча дія g(t)=1(t), а збурення f(t)=2sin(·t). Структурна схема системи наведена на рисунку.

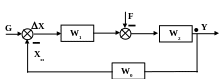
За таблицями визначаємо коефіцієнти похибки від задаючого впливу

за формулою

передатня функція для похибки від збурення (враховуючи знак впливу і зворотній зв"язок

За формулами для коефіцієнтів помилок знаходимо з допомогою передатньої функції замкнутої системи

17. Функція передачі незмінної частини САУ задається наступним виразом:

Розрахувати коректуючий пристрий, який забезпечує наступні показники якості –

w=feedback(tf([3],[0.01 0.52 1 0]),1);

figure(1)

step(w),grid;

K=3; T1=0.5; T2=0.02; Tpp=0.6; k0=0.6;

w1=0.1:0.001:(1/T1); w2=(1/T1):0.001:(1/T2); w3=(1/T2):0.001:100;

l1=20*log10(K)-20*log10(w1);

l2=20*log10(K)-20*log10(w2)-20*log10(T1*w2);

l3=20*log10(K)-20*log10(w3)-20*log10(T1*w3)-20*log10(T2*w3);

Tzr = 1/((k0*pi)/Tpp)

T02 = 1/(3*(1/Tzr))

T01 = 1/(((1/Tzr)*(1/Tzr))/(1/T02))

Tb1=1/1.0

w5=0.1:0.001:(1/Tb1); w6=(1/Tb1):0.001:(1/T01); w7=(1/T01):0.001:(1/T02); w8=(1/T02):0.001:(1/T2); w4=(1/T2):0.001:100;

l5=20*log10(K)-20*log10(w5);

l6=20*log10(K)-20*log10(w6)+20*log10(Tb1*w6);

l7=20*log10(K)-20*log10(w7)+20*log10(Tb1*w7)-20*log10(T01*w7);

l8=20*log10(K)-20*log10(w8)+20*log10(Tb1*w8)-20*log10(T01*w8)-20*log10(T02*w8);

l4=20*log10(K)-20*log10(w4)+20*log10(Tb1*w4)-20*log10(T01*w4)-20*log10(T02*w4)-20*log10(T2*w4);

Tk1=Tb1

Tk2=T01

Tk3=T1

Tk4=T02

K=1;

w9=0.1:0.001:(1/Tk1); w10=(1/Tk1):0.001:(1/Tk2); w11=(1/Tk2):0.001:(1/Tk3); w12=(1/Tk3):0.001:(1/Tk4); w13=(1/Tk4):0.001:100;

l9=20*log10(K)-20*log10(w9)+20*log10(w9);

l10=20*log10(K)-20*log10(w10)+20*log10(w10)+20*log10(Tk1*w10);

l11=20*log10(K)-20*log10(w11)+20*log10(w11)+20*log10(Tk1*w11)-20*log10(Tk2*w11);

l12=20*log10(K)-20*log10(w12)+20*log10(w12)+20*log10(Tk1*w12)-20*log10(Tk2*w12)+20*log10(Tk3*w12);

l13=20*log10(K)-20*log10(w13)+20*log10(w13)+20*log10(Tk1*w13)-20*log10(Tk2*w13)+20*log10(Tk3*w13)-20*log10(Tk4*w13);

figure(2)

semilogx(w1,l1,w2,l2,w3,l3,w4,l4,w5,l5,w6,l6,w7,l7,w8,l8,w9,l9,w10,l10,w11,l11,w12,l12,w13,l13),

grid

Визначити прямий та інверсний комплексний коефіцієнт підсилення двохпозіційного реле з додатнім гістерезисом. На вхід НЕ надходить гармонійний сигнал. Релейний елемент має поріг спрацювання ±Х_а = ±0,4 В, вихідний сигнал релейного елемента після спрацювання дорівнює ±Z_а= ±2 В. Побудувати графіки розрахованих характеристик.

Характеристика реле з додатнім гістерезисом має наступний вигляд:

Реакція реле на гармонійний вхідний сигнал

Дійсна та уявна частини комплексного коефіцієнта підсилення:

Комплексний коефіцієнт підсилення

Інверсний коефіцієнт підсилення

24. Визначити прямий та інверсний комплексний коефіцієнт підсилення нелінійного елемента типу обмеження з зоною нечутливості. На вхід НЕ надходить гармонійний сигнал. Зона нечутливості обмежена праметром ±Х_а=±0,5 В, вихідний сигнал НЕ дорівнює ±Z_а=±3,5 В. Побудувати графіки розрахованих характеристик.

Характеристика нелінійного елемента:

Реакція реле на гармонійний вхідний сигнал

Дійсна та уявна частини комплексного коефіцієнта підсилення:

Комплексний коефіцієнт підсилення

Інверсний коефіцієнт підсилення