21. Розвязати задачу графічним методом
Z = x1+2x2 → min , max
на графіку
проходять три прямі
В напрямку вектора n точкою мінімуму є точка В(3;0) Zmin = 3+0=3
Точкою максимуму є точка К , знайдемо її координати шляхом розвязку системи :
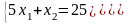
22. Розвязати задачу симплекс методом
z = x1 + x2 + 5x3 + x4 +2x5 min
Xi ≥ 0
Використовую метод додаткових змінних
Xi ≥ 0
|
|
1 |
1 |
5 |
1 |
2 |
0 |
0 |
|
0 |
Х6 |
1 |
3 |
2 |
1 |
5 |
1 |
0 |
10 |
0 |
Х7 |
1 |
4 |
3 |
2 |
11 |
0 |
1 |
11 |
|
|
1 |
1 |
5 |
1 |
2 |
0 |
0 |
Z=0 |
Оскільки всі приведені коефіціенти набули потрібного знаку (всі із знаком “+”), це означає що розв’язок задачі на min завершено. Z min = 0
Досягається в точках
23.Поставити задачу двоїсту до заданої
z=x1+3x2+x3+4x4+x5 min
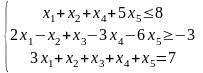
Х2,Х5≥0
Х2,Х5≥0
F = 8y1+3y2+7y3→ mах
y1, y2 ≥0
24. Знайти екстремуми функції.
f(x,y,z)=xy+5xz+6zy при умові xyz=20
f(x,y)=xy+100/y + 120/x
;
x/y=120/100
; x=1,2y
1,44y3=120
y3=120/1,44;
;
;
,
,
;
т. А (5,241; 4,368; 0,874)
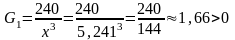
G2=1,667 * 2,4 – 1 = 4-1 = 3>0;
Матриця є додатньо визначеною, т.А(5,241; 4,368; 0,874) є точкою строгого локального мінімуму
f(x, y, z) обчислюю за допомогою Mathcad
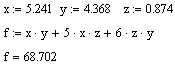
25. знайдемо екстремуми функцій f(x,y)=x2+5xy+2y2+5z2+6xz+7yz+4x+8y+10y:
f(x,y, z)= x2+5xy+2y2+5z2+6xz+7yz+4x+8y+10y
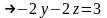
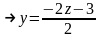
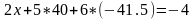
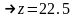
знайдемо 2-гі похідні
,
,
,
,
,
,
Досліджуємо точку А(22,5; 40; -41,5)
G1=2>0,
G2=8-25=-17<0,
G3=80+28+250-144-210-210=
-206<0
Матриця є від’ємно визначеною, тому точка А є стаціонарною точкою, а екстремуму не має.
По ходу так але я точно не знаю, тому що G3<0
26. Знайти умовний екстремум
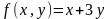
Знайдемо даний екстремум за методом Лагранжа
→
→
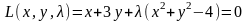
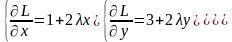
А
:
B:
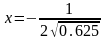
A:
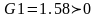
т. А є точкою строгого локального мінімуму
В:
т. В є точкою строгого локального максимуму
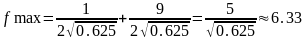
27. Розвязати гру, задану матрицею:
α=max(-4;
-7)=-4 β=min(20;
9)=9
,
гра розв’язується в змішаних стратегіях.
- ціна гри.
Визначаю частоти використання стратегій ( , ) та ціну гри ( ).
=>
=>
=>
=>
=>
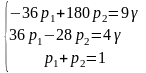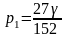
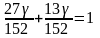Відношення
частоти використання стратегії А1
p1
до
А2
p2
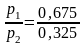
тобто стратегія А1 використовуеться 2 рази частіше ніж А2 хоча стратегія А1 не допускае ні великого програшу (-4) ні великого виграшу(9) а стратегія А2 є ризикованою, є великий виграш 20 але і велий програш -7.