5. Исследование характеристик исходной

системы в замкнутом состоянии.

1. Разработка модели исходной системы в замкнутом состоянии.

Перейдем к анализу характеристик замкнутой системы. Чтобы получить модель замкнутой системы достаточно дополнить имеющуюся модель цепью обратной связи (рис. 9). Причем, сигнал с выхода блока 8 нужно подать на отрицательный вход усилителя – блок 1.

Рис. 9

2. Построение и анализ графика переходного процесса по управляющему воздействию в замкнутой системе.

Для получения графика переходного процесса нужно задать вход на блок 9. График переходного процесса по управляющему воздействию в замкнутой САУ приведен на рис. 10. Переходный процесс имеет вид колебаний с нарастающей амплитудой, следовательно, замкнутая система неустойчива.

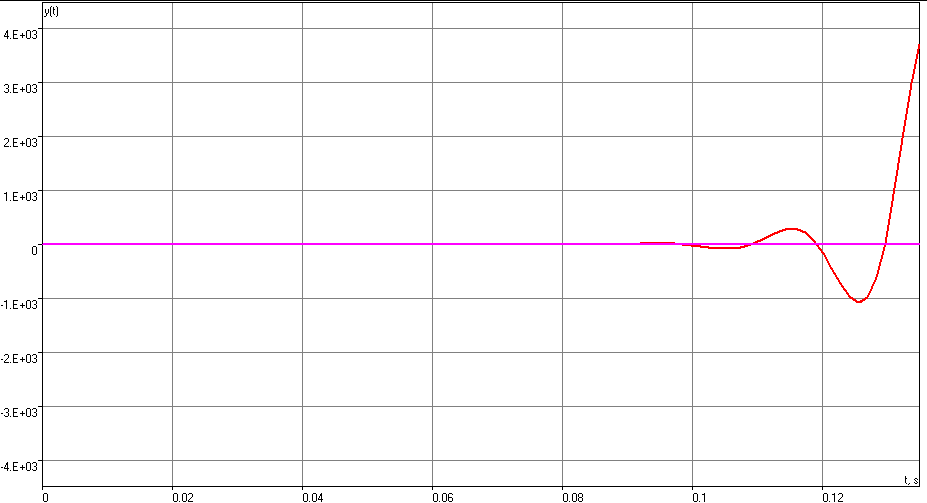
Рис. 10 - График переходного процесса по управляющему воздействию в замкнутой САУ

3. Анализ графика расположения корней характеристического уравнения замкнутой системы.

Расчетный график расположения корней характеристического уравнения (полюсов) передаточной функции замкнутой системы приведен на рис. 11.

Рис. 11 - График расположения корней характеристического уравнения

замкнутой системы

Из графика на рис. 11 следует, что 2 корня характеристического уравнения замкнутой системы расположены в правой полуплоскости, следовательно, замкнутая система неустойчива.

Таким образом, исследование замкнутой системы по различным критериям свидетельствует о ее неустойчивости.

6. Исследование характеристик замкнутой скорректированной системы с пи – регулятором.

Чтобы обеспечить устойчивость замкнутой системы введем в систему ПИ-регулятор.

1. Расчет параметров ПИ – регулятора.

По методике, изложенной в работе № 4 [1], выбираем параметры ПИ-регулятора.

ПИ-регулятор имеет ПФ

.

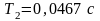Среди постоянных времени системы можно выделить «большую» , «среднюю» и «малую» .

Принимаем постоянную времени в числителе регулятора, равной наибольшей постоянной времени

T_1РЕГ= T₁ =0,19 с.

Средней постоянной времени является постоянная T₂ =0,0358 c. Значение постоянной времени интегрирующего звена регулятора рассчитываем по выражению (2.3), приняв b=2

T_И.РЕГ=b∙k_ИСХT₂=2·48,6·0,0358=4,53 с.

2. Построение и анализ графика переходного процесса по управляющему воздействию в системе с ПИ-регулятором.

Модель системы остается прежней. Только, в блоке 7 теперь задаем передаточную функцию ПИ-регулятора в виде

.

Чтобы получить переходный процесс для изменения частоты вращения, назначаем выход на блок 5, вход на блок 9. Коэффициент передачи блока 9 принимаем k₉ = k_BR=1.3.

Переходный процесс по управляющему воздействию показан на рис. 12. Частота вращения двигателя стремится к установившемуся значению, следовательно, замкнутая система с ПИ-регулятором устойчива.

Как следует из полученных данных, перерегулирование составляет 6,7%, время переходного процесса равно 0,34с. Как рассчитано выше,

время переходного процесса в разомкнутой системе составляет 0,90с. Таким образом, время переходного процесса в замкнутой системе по сравнению с разомкнутой существенно уменьшилось.

Э

. 3. Построение и анализ графика переходного процесса по возмущению в системе с ПИ-регулятором.

Для расчета переходного процесса необходимо перенести вход на блок 10. График переходного процесса приведен на рис. 13. При скачке возмущения частота вращения двигателя после динамического провала, равного 3,5 рад/с, стремится к исходному значению. Иными словами, статическая ошибка в системе равна 0.Ъ

\

ХЭ ТЛБО

Таким образом, в замкнутой системе с выбранным ПИ-регулятором за счет компенсации «большой» постоянной время переходного процесса по управляющему воздействию удалось уменьшить, по сравнению с разомкнутой системой. Кроме того, использование ПИ-регулятора позволило свести к нулю статическую ошибку в поддержании скорости.

Рис. 12 –Переходный процесс по управляющему воздействию в замкнутой САУ с ПИ-регулятором

Рис. 13–Переходный процесс по возмущающему воздействию

в замкнутой САУ с ПИ-регулятором

Остановимся на вопросе технической реализации ПИ-регулятора.

Схема пропорционально–интегрального регулятора (ПИ–регулятора) приведена на рисунке 14.

Рис. 14 - Схема ПИ–регулятора

Сравнивая приведенную схему со схемой П-регулятора (рис.1), несложно заметить, что они отличаются только тем, что в цепи обратной связи операционного усилителя последовательно включены резистор R3 и емкость С. Значение сопротивлений и емкости в цепях регулятора рассчитывается на основе найденных значений постоянных времени регулятора [2].

Таким образом, выполненные достаточно сложные расчеты по исследованию характеристик замкнутой системы приводят к простому техническому решению: чтобы обеспечить устойчивость и высокое качество переходных процессов в замкнутой САУ, в схему регулятора достаточно включить дополнительную емкость.